3.135 FAQ-782 Why parameter's standard error remains the same when error bar largely changes?Chi-Se-Remain
Last Update: 1/16/2025
To keep the fitted parameter's Standard Error (SE) and related results compatible with other software, the Scale Error with sqrt(Reduced Chi-Sqr) box is checked by default. With this checkbox checked, the parameter's SE remains the same even though error bars are changed largely. We recommend unchecking this option when fitting data with Instrumental, Arbitrary Dataset or Direct Weighting, so that parameter's SE can reflect the magnitude of weight.
You can find Scale Error with sqrt(Reduced Chi-Sqr) option in
| Note:
This checkbox ONLY affects SE of fitted parameters. It does NOT affect the fitting process or the parameter values in any way.
|
Simple theory explanation
We discuss below how SE of the jth fitted parameter 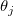 changes with or without Scale Error with sqrt(Reduced Chi-Sqr) checked. For simplification, we assume that the error bar changes with or without Scale Error with sqrt(Reduced Chi-Sqr) checked. For simplification, we assume that the error bar  is scaled by multiplied by a constant k. For more detailed algorithm and explanation, please refer to the theory of Nonlinear Curve Fitting. is scaled by multiplied by a constant k. For more detailed algorithm and explanation, please refer to the theory of Nonlinear Curve Fitting.
By default, when the Scale Error with sqrt(Reduced Chi-Sqr) is enabled, the variance-convariance matrix 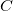 for parameters for parameters 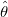 depends on both depends on both 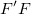 and and 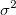 . .
Where 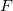 is the partial derivative matrix, whose element in ith row and jth column is: is the partial derivative matrix, whose element in ith row and jth column is:
and 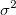 is the mean residual variance, which is estimated by Reduced Chi-Sqr: is the mean residual variance, which is estimated by Reduced Chi-Sqr:
SE of 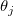 is then the square root of a main diagonal value of matrix is then the square root of a main diagonal value of matrix 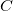
If the error bars  is changed by a constant k, both is changed by a constant k, both 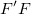 and and 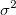 will be changed by a factor will be changed by a factor 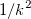 , then k will cancel each other out in the calculation of SE. Thus, SE remains unchanged when error bar is scaled. , then k will cancel each other out in the calculation of SE. Thus, SE remains unchanged when error bar is scaled.
If Scale Error with sqrt(Reduced Chi-Sqr) is unchecked, which means 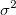 is excluded when calculating the variance-convariance matrix, the matrix is excluded when calculating the variance-convariance matrix, the matrix 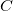 depends on depends on 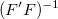 only. only.
SE now becomes
If the error bars are multiplied by k, SE will be k times as well.
After fitting the models, we use the reduced chi-sqr to check whether the weights can represent the real Y error or not. In brief, if you find parameter's standard error is greatly different when you check or uncheck the Scale Error with sqrt(Reduced Chi-Sqr) option, it means the weights may not represent the real y errors. For details, please refer to this page.
Quick Example
Below is a quick example verifying that Scale Error with sqrt(Reduced Chi-Sqr) effects the fitted parameters' SE only.
- Copy this data and paste it into a worksheet.
- Right click col(C) and select Set As: Y Error.
- Highlight all columns and select Analysis: Fitting: Nonlinear Curve Fit to open the Nonlinear Fit dialog.
- Select Gauss from Function drop-down list. Select Advanced tab and expand Fit Control branch. Make sure Scale Error with sqrt(Reduced Chi-Sqr) is checked.
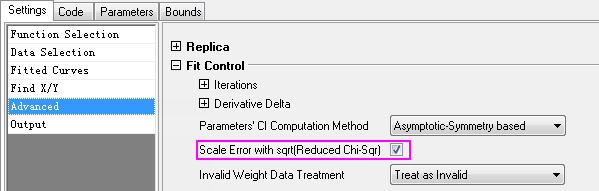
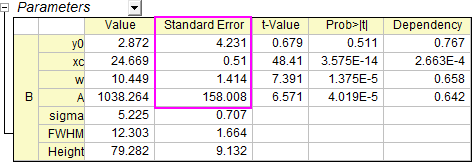
Click Fit will generate the fitting report, which contains parameter values and SE.
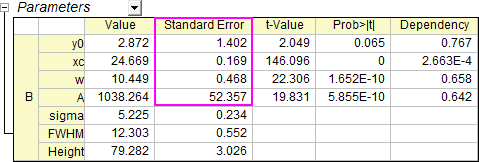
- Click the green lock and select Change Parameters. In the Nonlinear Fit dialog that opens, uncheck Scale Error with sqrt(Reduced Chi-Sqr).
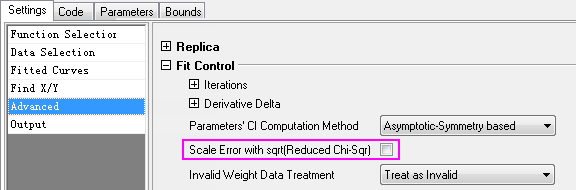
Click Fit. SE of the parameters change but the fitted values do not.
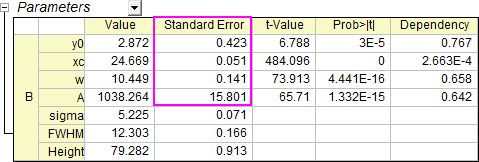
- Now we are going to scale the error and see how it effects SE with Scale Error with sqrt(Reduced Chi-Sqr) checked or unchecked. Open Nonlinear Fit dialog by Change Parameters. Check the Scale Error with sqrt(Reduced Chi-Sqr) and change Recalculate to Auto.
- Multiply the error column C by 10. The report sheet will be updated automatically. You will see SE of the parameters remain the same (compare to the second image in step 4).
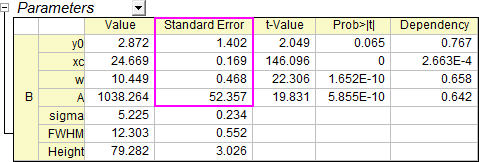
- Open Nonlinear Fit dialog by Change Parameters again. Uncheck Scale Error with sqrt(Reduced Chi-Sqr). Click Fit. You will see SE is multiplied by 10 this time.
Sample data
| X
|
Y
|
Y Error
|
| 11
|
5
|
0.4472
|
| 13
|
10
|
0.6324
|
| 15
|
19
|
0.8718
|
| 17
|
27
|
1.0392
|
| 19
|
49
|
1.4
|
| 21
|
65
|
1.6124
|
| 23
|
77
|
1.755
|
| 25
|
80
|
1.7888
|
| 27
|
77
|
1.755
|
| 29
|
59
|
1.5362
|
| 31
|
44
|
1.3266
|
| 33
|
24
|
0.9798
|
| 35
|
11
|
0.6634
|
| 37
|
14
|
0.7484
|
| 39
|
4
|
0.4
|
Related Topics
Keywords:Fitting, Standard Error, Reduced Chi-Sqr, Error Variance
|