3.17 FAQ-242 Why is my Reduced Chi-Sqr value very different from 1?Bad-ReducedChiSqr
Last Update: 8/8/2018
The Nonlinear Curve Fitter tool in Origin computes and reports Reduced Chi-Sqr value as one of the measures of goodness of fit. If a weight is included in the fitting process and the Reduced Chi-Sqr is very different from 1, please examine if an improper weighting method is chosen. If the Reduced Chi-Sqr value is much smaller than 1, it may indicate a too large weight. Vice versa.
Typically Reduced Chi-Sqr value is closer to 1, better a fit we get. If weight is involved during fitting, Reduced Chi-Sqr close to 1 also indicates that the difference between observed data and fitted data has a similar magnitude of weight. When fitting with weight, Reduced Chi-Sqr is calculated as follow:
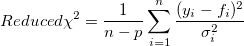
where n is the number of data, p the degree of freedom, 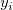 the ith y data, and the ith y data, and 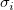 the ith error. When the number of data is large enough, n - p approaches n, and Reduced Chi-Sqr is determined by the difference between source data and fitted data and the weight. the ith error. When the number of data is large enough, n - p approaches n, and Reduced Chi-Sqr is determined by the difference between source data and fitted data and the weight.
Therefore, if Reduced Chi-Sqr is very different from 1, it may indicate an improper weighting method. Origin provides several weighting methods, please refer to this page for formula of each method. If the Reduced Chi-Sqr value is much smaller than 1, it may indicate a too large weight. Vice versa.
If you perform a nonlinear curve fit with the Statistical weighting method on a set of data and it generates a fitting result of Reduced Chi-Sqr close to 1, it indicates the fit result is good. Then you scale the y data by multiplied a factor of 10. Note that the Statistical weighting method takes ~y magnitude as error variation, the weight is also scaled by 10. However, for a random variable 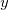 with weight with weight 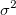 , the proper weight for , the proper weight for 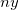 should be should be
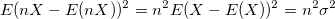 . .
So the Statistical cannot calculate a proper weight for the scaled data. The Redcued Chi-Sqr value which is scaled much larger than 1 also indicates this improper. To make Redcued Chi-Sqr close to 1 again, you should choose Instrumental or Variance ~ y^2 method, which take ~y^2 magnitude as weight.
| Note:
In addition to Reduced Chi-Sqr, Origin outputs many other quantities such as R-Square and Adjusted R-Square which can also be used to estimate goodness of fit.
|
Keywords:goodness, chi-square, residual sum of squares, fit, fitting, nonlinear, variance
|