16.9 DifferentiateMath-Differentiate
Overview
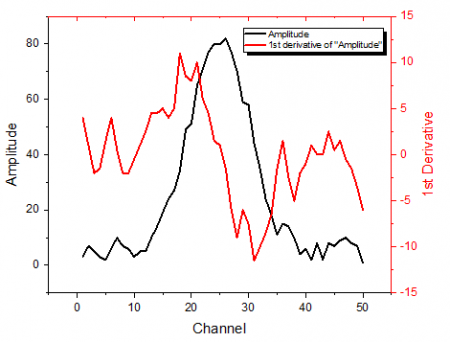
This function performs simple derivative calculations on a data set. The derivative at a given point is computed by taking the average of the slopes between the point and its two closest neighbors. Missing values are ignored.
For evenly-spaced X data, you can apply Savitzky-Golay smoothing. If the X data are not equally spaced, this method may not produce a reliable result.
To Use Differentiate Tool
- Create a new worksheet with data.
- Highlight the desired column.
- Select Analysis: Mathematics:Differentiate from the Origin menu to open the differentiate dialog. The X-Function differentiate is called to perform the calculation.
Dialog Options
| Recalculate
|
Controls recalculation of analysis results
For more information, see: Recalculating Analysis Results
|
| Input
|
Specify the input XY range (curve).
For help with range controls, see: Specifying Your Input Data
|
| Derivative
|
Specify the derivative order.
|
| Smooth
|
Specify smoothing method.
- Savitzky-Golay Smooth
- Use the Savitzky-Golay smoothing method.
- Polynomial Order
- This is available only when the smoothing is chosen. Set the polynomial order (1 to 9) for the Savitzky-Golay smoothing method.
- Points of Window
- This is available only when the smoothing is chosen. Set the window size used in the Savitzky-Golay smoothing.
|
| Output
|
Specify the output range.
For help with the range controls, see: Output Results
|
| Plot Derivative Curve
|
Specify whether to plot the derivative curve.
|
Algorithm
The derivative of a function is defined as:

While the 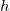 is small enough, we can use a centered difference formula to approximate the derivative: is small enough, we can use a centered difference formula to approximate the derivative:
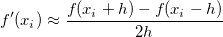
In practice, Origin treats discrete data by the transform of the centered difference formula, and calculates the derivative at point 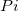 by taking the average of the slopes between the point and its two closest neighbors. by taking the average of the slopes between the point and its two closest neighbors.
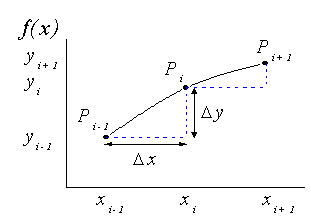
The derivative function applied to discrete data points can therefore be written:
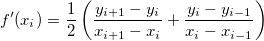
When smooth option is chosen in differentiate, and X data is evenly spaced, Savitzky-Golay method will be used to calculate the derivatives.
First perform a polynomial regression on the data points in the moving window. The polynomial value at position x can be calculated as:
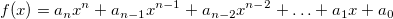 . .
where n is the polynomial order, and 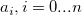 are fitted coefficients. are fitted coefficients.
And 1st order derivative at position x is:
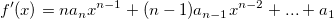 . .
|