16.14 InverseMath-Inverse
Description
The minverse X-Function generates an inverse matrix by dividing the adjoint by its determinant. When matrices do not have inverses or determinants, a Moore-Penrose pseudoinverse is computed.
For user-interface access to this function:
- Create a new matrix with data.
- Activate the matrix.
- Select Analysis: Mathematics: Inverse to open the minverse dialog box.
Dialog Options
Algorithm
For a square matrix of full rank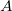 , the inverse matrix , the inverse matrix 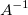 (aka the reciprocal matrix), will satisfy the relationship: (aka the reciprocal matrix), will satisfy the relationship:
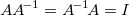
where 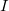 is the identity matrix. is the identity matrix.
The calculation of 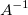 can be expressed as: can be expressed as:
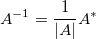
where 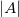 is the determinant of matrix is the determinant of matrix 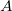 and and 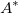 is the adjoint. is the adjoint.

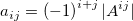
where 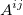 is the is the 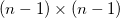 matrix by elimination of the matrix by elimination of the 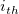 column and column and 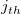 row of row of 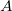 . .
When matrices do not have inverses or determinants, a Moore-Penrose pseudoinverse will be computed. It exists for any 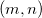 matrix. matrix.
Given an 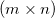 matrix matrix 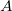 , , 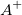 is the unique is the unique 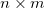 pseudoinverse matrix. If pseudoinverse matrix. If 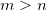 and A has full rank, then the and A has full rank, then the 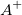 satisfies the following: satisfies the following:
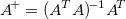
The computation is based on singular value decomposition (SVD) of the matrix 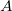 and any singular values within tolerance, are treated as zero. If the rank of and any singular values within tolerance, are treated as zero. If the rank of 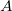 is not full, then the matrix will shrink to a smaller matrix. is not full, then the matrix will shrink to a smaller matrix.
References
- 1. E. H. Moore: On the reciprocal of the general algebraic matrix. Bulletin of the American Mathematical Society 26, 394-395 (1920).
- 2. Roger Penrose: A generalized inverse for matrices. Proceedings of the Cambridge Philosophical Society 51, 406-413 (1955).
|