DifferenzierenMath-Differentiate
Beschreibung
Diese Funktion führt einfache Ableitungsberechnungen für einen Datensatz durch. Die Ableitung an einem Punkt wird berechnet, indem der Durchschnitt der Steigungen zwischen dem Punkt und den zwei nächsten Nachbarn genommen wird. Fehlende Werte werden ignoriert. Für äquidistant verteilte X-Daten können Sie die Glättungsmethode Savitzky-Golay anwenden. Wenn die X-Daten nicht äquidistant verteilt sind, ergibt diese Methode vielleicht kein zuverlässiges Ergebnis. Um diese Funktion zu verwenden:
- Öffnen Sie ein neues Arbeitsblatt mit Daten.
- Markieren Sie die gewünschte Spalte.
- Wählen Sie Analyse: Mathematik: Differenzieren im Origin-Menü, um das Dialogfeld differentiate zu öffnen. Die X-Funktion differentiate wird aufgerufen, um die Berechnung durchzuführen.
Dialogoptionen
| Neu berechnen |
Bedienelemente zur Neuberechnung der Analyseergebnisse
Weitere Informationen finden Sie unter Analyseergebnisse neu berechnen.
|
| Eingabe |
Legen Sie den XY-Eingabedatenbereich (Kurve) fest. Hilfe zum Festlegen von Bereichen finden Sie hier: Eingabedaten festlegen
|
| Ableitung |
Legen Sie die Ableitungsordnung fest.
|
| Glätten |
Legen Sie die Glättungsmethode fest.
- Savitzky-Golay-Glättung
- Legen Sie fest, ob die Savitzky-Golay-Glättungsmethode verwendet werden soll.
- Polynomielle Ordnung
- Diese Option ist nur verfügbar, wenn die Glättung gewählt ist. Sie legt die polynomielle Ordnung (1 bis 9) für die Savitzky-Golay-Glättungsmethode fest.
- Punkte der Fenster
- Diese Option ist nur verfügbar, wenn die Glättung gewählt ist. Legen Sie die Fenstergröße fest, die für die Savitzky-Golay-Glättung verwendet wird.
|
| Ausgabe |
Legen Sie den Ausgabebereich fest. Hilfe zum Festlegen der Bereiche finden Sie unter: Ergebnisse ausgeben
|
| Ableitungskurve zeichnen |
Legen Sie fest, ob die Ableitungskurve gezeichnet werden soll.
|
Algorithmus
Die Ableitung einer Funktion wird definiert als: 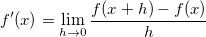
Während 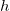 klein genug ist, können wir eine zentrierte Formel für die Differenziation verwenden, um die Ableitung zu approximieren: klein genug ist, können wir eine zentrierte Formel für die Differenziation verwenden, um die Ableitung zu approximieren: 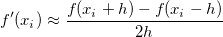
Origin bearbeitet diskrete Daten in der Praxis durch die Transformation der zentrierten Differenziationsformel und berechnet die Ableitung an Punkt 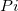 , indem der Durchschnitt der Steigungen zwischen dem Punkt und seinen zwei nächsten Nachbarn genommen wird. , indem der Durchschnitt der Steigungen zwischen dem Punkt und seinen zwei nächsten Nachbarn genommen wird. 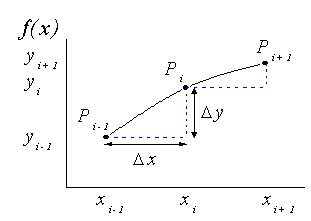
Die Ableitungsfunktion, die auf diskrete Datenpunkte angewendet wird, kann daher folgendermaßen geschrieben werden: 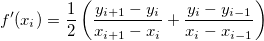
Wenn die bei der Differenziation verwendete Glättung für  äquidistant verteilt ist, verwenden die Savitzky-Golay-Methode, um die Ableitungen zu berechnen. äquidistant verteilt ist, verwenden die Savitzky-Golay-Methode, um die Ableitungen zu berechnen. Zuerst ergibt sich durch Interpolation eine 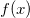 : : 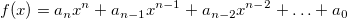
Die Ableitung von 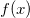 ist dann: ist dann: 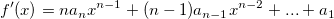
Referenzen
|