InverseMath-Inverse
Beschreibung
Die X-Funktion minverse erzeugt eine inverse Matrix, indem Sie die Adjunkte durch ihre Determinante teilt. Wenn Matrizen keine Inversen oder Determinanten haben, wird eine Moore-Penrose-Pseudoinverse berechnet. Zugriff auf diese Funktion über die Bedienoberfläche:
- Öffnen Sie eine neue Matrix mit Daten.
- Aktivieren Sie die Matrix.
- Wählen Sie Analyse: Mathematik: Inverse, um den Dialog minverse zu öffnen.
Dialogoptionen
| Neu berechnen |
Bedienelemente zur Neuberechnung der Analyseergebnisse
Weitere Informationen finden Sie unter Analyseergebnisse neu berechnen.
|
| Eingabematrix |
Legen Sie die Eingabematrix fest. Hilfe zum Festlegen von Bereichen finden Sie hier: Eingabedaten festlegen
|
| Ausgabematrix |
Legen Sie fest, wo die inverse Matrix ausgegeben wird. Hilfe zum Festlegen der Bereiche finden Sie unter: Ergebnisse ausgeben
|
Algorithmus
Für eine Quadrat- und Rangmatrix von 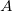 erfüllt die inverse Matrix erfüllt die inverse Matrix 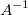 , die auch als reziproke Matrix bezeichnet wird, wird folgendes Verhältnis: , die auch als reziproke Matrix bezeichnet wird, wird folgendes Verhältnis: 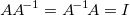
wobei 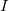 die Identitätsmatrix ist. die Identitätsmatrix ist. Die Berechnung von 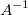 kann ausgedrückt werden mit: kann ausgedrückt werden mit: 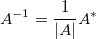
wobei 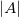 die Determinanten der Matrix die Determinanten der Matrix 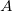 meint, und meint, und 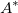 die Adjunkte ist von die Adjunkte ist von 
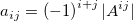
wobei 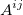 die Matrix die Matrix 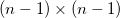 ist, indem die Spalte ist, indem die Spalte 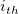 und Zeile und Zeile 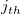 aus aus 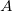 entfernt wird. entfernt wird. Wenn Matrizen keine Inversen oder Determinanten haben, wird eine Moore-Penrose-Pseudoinverse berechnet. Sie existiert für jede 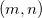 Matrix. Matrix. Bei einer gegebenen 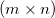 Matrix Matrix 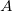 , ist , ist 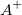 die eindeutige die eindeutige 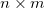 pseudoinverse Matrix. Wenn pseudoinverse Matrix. Wenn 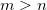 und A vollen Rang haben, dann erfüllt und A vollen Rang haben, dann erfüllt 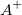 Folgendes: Folgendes: 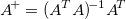
Die Berechnung basiert auf einer singulären Wertzerlegung (SVD) der Matrix 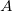 . Jeder singuläre Wert innerhalb der Toleranz wird als Null behandelt. Wenn der Rang von . Jeder singuläre Wert innerhalb der Toleranz wird als Null behandelt. Wenn der Rang von 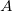 nicht voll ist, schrumpft die Matrix zu einer kleineren Matrix. nicht voll ist, schrumpft die Matrix zu einer kleineren Matrix.
Referenzen
- 1. E. H. Moore: On the reciprocal of the general algebraic matrix. Bulletin of the American Mathematical Society 26, 394-395 (1920).
- 2. Roger Penrose: A generalized inverse for matrices. Proceedings of the Cambridge Philosophical Society 51, 406-413 (1955).
|