2D補間/補外Math-2D-Inter-Extrapolate
概要
2D補間/補外を使用すると、既存のXYZデータに対しての特定のXYデータセットの補間/補外や、特定の行列オブジェクトに対しての補間/補外が可能です。
XYからの補間
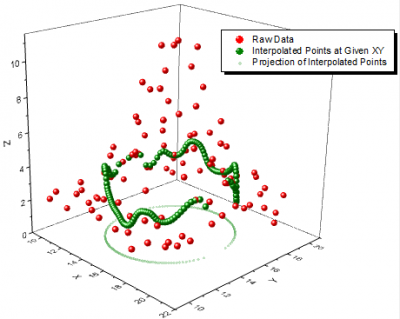
XYからZを補間ツールを使用すると、補間/補外のためにXY値のセットを指定できます。これにより、不等間隔のXYデータセットの2D補間/補外における追加の自由度を提供します。Originは、XYからZを補間するための8つの補間手法をサポートしています:近傍、ランダムKriging法、ランダムRenka Cline法、ランダムShepard法、ランダムTPS法、スプライン、三角、加重平均法
XYからZを補間するには
- 入力データを含むワークブックをアクティブにします。
- メニューから解析:数学:XYからZを補間を開きます。すると、interp2ダイアログボックスが開きます。
- 入力オプションを設定して、OKをクリックします。interp2Xファンクションが呼び出されて計算を実行します。
XYからZを補間するためのダイアログオプション
XYからZを補間するためのダイアログコントロールの詳細については、X functionのドキュメントinterp2を参照してください。
行列の2D補間
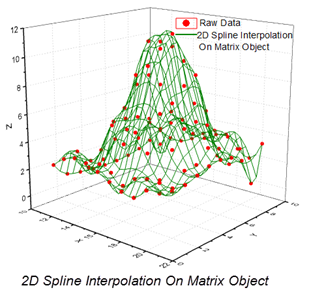
2次元の補間/補外は、Originの行列に保存されているデータに対しても実行可能です。Originは、行列を補間するための5つの補間手法をサポートしています:近傍、Bilinear、Bicubic、スプライン、BiquadraticXとYの補間出力範囲を指定することも可能です。
行列で2D補間するには
- 入力データを含む行列をアクティブにします。
- メニューから、解析:数学:2D補間/補外を選択します。minterp2ダイアログボックスが開きます。
- 入力オプションを設定して、OKをクリックします。minterp2Xファンクションが呼び出されて計算を実行します。
行列で2D補間するためのダイアログオプション
| 再計算
|
分析結果の再計算の設定を変更します。
詳細情報は、 分析結果の再計算をご覧下さい。
|
| 入力行列
|
補間/補外を行うデータを含む行列を指定します。
範囲の設定に関する詳細は、入力データを指定するをご覧ください。
|
| 手法
|
補間/補外の手法を指定します。
- 近傍
- 最近傍の点を使用して補間
- Bilinear(共一次補間)
- 2次線形補間
- Bicubic Convolution
- 2次キュービック補間
- スプライン
- 2次スプライン補間
- Biquadratic(共二次補間)
- 2次双補間
- Bicubic Lagrange
- Lagrange多項式を用いた2次補間
|
| 列数
|
出力行列の列数を指定します。
|
| 行数
|
出力行列の行数を指定します。
|
| 欠損値の前処理
|
2D補間で欠損値を前処理する方法を指定します
- スキップ
- 最初に欠損値をすべて削除してから、補間を実行します。
- Renka Clineで補間
- Renka Cline: 任意の点P について、P を含む三角形の3つの頂点のそれぞれで、データ値と勾配推定値を使用して補間値を計算します。
|
| 座標
|
出力行列の座標値/XYマッピングを指定します。
- 最初のX
- 出力行列の最初のX値
- 最後のX
- 出力行列の最初のX値
- 最初のY
- 出力行列の最初のY値
- 最後のY
- 出力行列の最後のY値
|
| 出力行列
|
補間/補外したデータの出力行列を指定します。
|
行列の補間のアルゴリズム
近傍(最近傍)補間:
最も近いグリッドポイントを使用して補間値を計算します。
多項式補間:
Bilinear、Biquadratic、Bicubic、Bicubic Lagrangeの手法があり、同じように動作します。例えば、Biquadratic 補間法で 点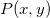 における値を計算するには、最初に、データポイント における値を計算するには、最初に、データポイント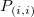 , , 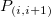 , , 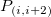 に基づいて、1Dの二次補間を垂直に実行して に基づいて、1Dの二次補間を垂直に実行して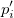 を作成し、同じ を作成し、同じ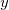 値を持つ 値を持つ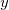 を生成します。そして を生成します。そして 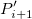 と と 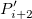 を計算します。値 を計算します。値 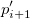 , , 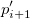 , , 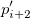 は、 は、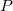 を通る直線を定義します。次に、1Dの二次補間を水平に実行し、 を通る直線を定義します。次に、1Dの二次補間を水平に実行し、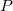 における値を計算します。 における値を計算します。
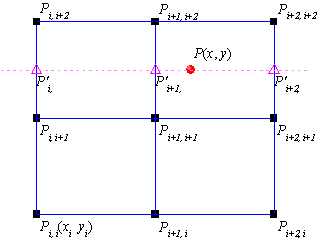
Bilinear、Biquadratic、Bicubic、Bicubic Lagrange 法の違いは、 次数の異なる多項式を使うことです。次数 n個の点を通る次数 n-1の補間多項式は、
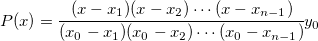
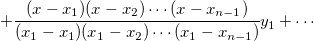
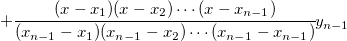
スブライン補間:
この方法は、次式によるbicubicスプライン 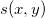 の値を計算します: の値を計算します:
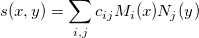
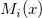 と と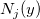 は正規化した3次B-スプラインを指し、 は正規化した3次B-スプラインを指し、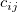 はスプラインの定数です。 はスプラインの定数です。
2次スプライン補間についての詳細は、NAG関数のドキュメントe02decをご覧ください。
参考文献
- Willian H. Press, etc. Numerical Recipes in C++, 2nd Edition.Cambridge University Press.(2002)
|