2.2.1.11 xyz_tps
Brief Information
Convert XYZ data to matrix using Thin Plate Spline gridding
Command Line Usage
1. xyz_tps iz:=Col(3);
2. xyz_tps iz:=Col(3) rows:=20 cols:=20;
3. xyz_tps iz:=Col(3) s:=0.8;
4. xyz_renka iz:=Col(3) om:=[MBook]MSheet!Mat(1);
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
iz
|
Input
XYZRange
|
|
Specifies the input XYZ range.
|
| Rows
|
rows
|
Input
int
|
35
|
Rows in the output matrix.
|
| Columns
|
cols
|
Input
int
|
35
|
Columns in the output matrix.
|
| Smoothing
|
s
|
Input
double
|
0.5
|
This is a non-negative value that specifies the extent to which the gridding surface will depart from the input data point. If the factor is zero, there will be no smoothing process and the interpolation surface will pass though all data points. A positive factor will make the surface smoother, but too large a factor will not preserve all the information of the original data.
|
| Outlier
|
outlier
|
Input
int
|
extrap
|
If the input data are irregular and do not completely fill a matrix by interpolation, this is a place to specify values for outlying points (see below)
Option list:
- extrap:Extrapolate
- Fills outliers with extrapolated-points based on the TPS algorithm (this is the default selection)
- missing:Missing Values
- Fills outliers with missing values
- zero:Zero
- Fills outliers with zeros
- min:Mimimum
- Fills outliers with the minimum value of the Z range
- max:Maximum
- Fills outliers with the maximum value of the Z range
- mean:Mean
- Fills outliers with the mean value of the Z range
- custom:Custom Value
- Fills outliers with a custom value.
|
| Outside
|
outside_val
|
Input
double
|
100
|
Specifies a custom value with which to fill the outliers of the results matrix. The user may specify a custom value only when the "Custom Value" option in the outlier field is selected.
|
| Tolerance
|
tolerance
|
Input
double
|
5E-3
|
Specifies the tolerance when determining whether or not the perimeter of input data is rectangular. This variable is not available when the "Extrapolate" option in outlier field is selected.
|
| Output Matrix
|
om
|
Output
MatrixObject
|
<new>
|
This is a place to configure the destination and format of output results, including name of the matrix worksheet.
See the syntax here.
|
| Regularization
|
r
|
Output
double
|
<unassigned>
|
The regularization parameter, which functions as the "weight" of bending energy. This parameter is proportional to the smoothing factor and takes effect only when smoothing factor is not zero. This is a parameter that is calculated based on the inputted smoothing factor.
|
Description
This function provides a method for random matrix conversion based on Thin Plate spline (TPS) algorithm, which can also be found in the XYZ Gridding dialog box.
TPS is a physical interpolation method. To generate gridding data, this method assumes that all the data points are distributed on a thin, elastic plate, or spline. The plate is constrained not to move at the grid points. The spline forms a 2-dimensional surface by spanning the grid points. The surface is deformed between the points to form a likely fit to the data. The best results are generally found by minimizing the so-called "bending energy function" of the spline.
The TPS method is suitable for 2D interpolation of locally flat surface.
Examples
- To run from the Command window
- Import the file \Samples\Matrix Conversion and Gridding\ XYZ Random Gaussian.dat.
- Type the command,
xyz_tps iz:=Col(3) rows:=50 cols:=50 and press Enter:
The matrix is graphed in a new window by image mode:
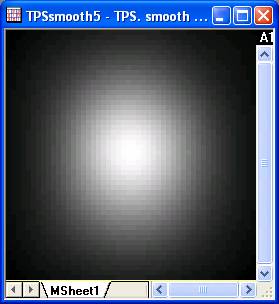
/*
This example shows how convert random worksheet data into matrix by TPS gridding method.
The sample data is exe_path\Samples\Matrix Conversion and Gridding\XYZ Random Gaussian.dat
1. Load data to a new created workbook.
2. Random xyz gridding by TPS method.
3. Plot a mesh graph.
*/
// Get sample data
fn$ = system.path.program$ + "Samples\Matrix Conversion and Gridding\XYZ Random Gaussian.dat";
newbook;
impASC fn$;
// Set the third column as Z column
wks.col3.type = 6;
// Convert worksheet data into matrix by TPS gridding method
xyz_tps 3 s:=1;
// Plot
worksheet -p 242 mesh;
Algorithm
The Thin Plate spline (TPS) algorithm is an interpolation scheme for scatter-data. The TPS process is analogous to fixing a thin, elastic "spline"(or surface) at the grid points, and lifting the surface through all the data points. The TPS algorithm builds a function that both captures all the data points and minimizes the so-called "bending energy function."
The bending energy function is defined as:
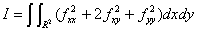 . .
And the minimizing function is of the form
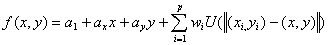 , ,
where 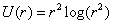 , and , and 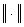 indicates the magnitude of a vector. indicates the magnitude of a vector.
The regularization parameter functions as the "weight" of the bending energy. A regularization parameter close to zero matches all data points closely, but creates a rough surface for noisy data. A larger regularization parameter smoothes data much more, but fits individual data points less strictly. Therefore, the regularization parameter indicates the strictness of interpolation requirements. This parameter is calculated based on the inputted Smoothing factor.
If we denote XYZ data points by 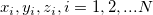 , then , then
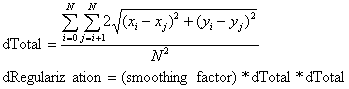
To find the minimum bending energy, more arithmetic transformations are required. Users who are interested in the algorithm details are encouraged to read the references for more information.
References
[1]. Bookstein, F. L. "Principal Warps: Thin Plate Splines and the Decomposition of Deformations." IEEE Trans. Pattern Anal. Mach. Intell. 11, 567-585 (1989)
[2]. Craven, P. and Wahba, G. "Smoothing Noisy Data with spline Functions". Numer. Math 31, 377-403 (1979).
[3]. Donato, Gianluca and Serge Belongie, "Approximation Methods for Thin Plate spline Mappings and Principal Warps" 2002.
Related X-Functions
xyz_regular, xyz_renka, xyz_renka_nag, xyz_shep, xyz_shep_nag, xyz_sparse
Keywords:worksheet, TPS
|