15.3.6.4 General Linear ConstraintsFitPara-General-Linear-Constraint
You can use general linear constraints to impose advanced constraints on the parameters, when the Enable Linear Constraints check box on the Code tab of NLFit dialog is enabled. Linear constraints can be defined in the Constraints box in the same tab or in the Fitting Function Organizer dialog:
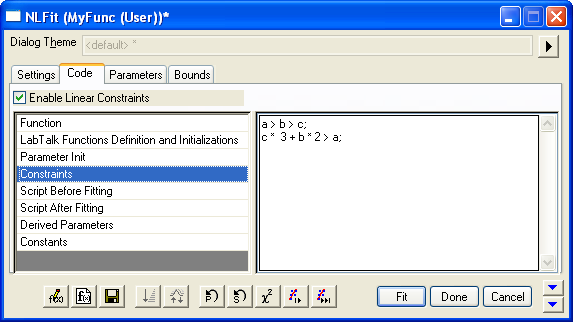
| Notes: The general linear constraints are only available to use for explicit fitting functions.
|
General Notation
To build linear constraints, you can use parameter names, arithmetic operators and relational operators. Five relational operators are supported: =, <, <=, >, and >=. Note that the curve fitter treats "<" and "<=" in the same way. Like wisely,
using ">" and using "=>" make no difference.
Below are some simple examples of linear constraints (suppose a, b, c, and d are parameters):
a > b;a + 2 * b >= c * 2 − d;a < b < c;a / 3 < 9;
If replica fitting is used, curve fitting will be performed to multiple peaks in the input data. In this case, the "ParaName__n" notation (with two underscores) can be used to refer to the parameter with the name ParaName for the nth peak when you define the linear constraints. For example, "w__1" and "w__2" will refer to the w parameters of the 1st and 2nd peaks respectively. To place a constraint that width of 2nd peak should be larger than width of the first, the linear constraint should be written as:
w__1 > w__2;
If global fitting is employed, you may use the the "ParaName_n" notation (with only one underscore) to refer to the parameter with the name ParaName for the nth dataset when you define the linear constraints.
When there are multiple lines of code in your linear constraint definition, please separate the lines with semicolons. Also, you can place multiple operators in a single sentence. For instance:
4 < a < b < 6;
This is equivalent to:
4 < a; a < b; b < 6;
You can also use variables that have been assigned to numeric values in linear constraints. For example, if the function has two parameters, P1 and P2, you can define a linear constraint as follows:
P1+qw*P2,
providing that you have previously set qw to a numeric value such as 2.5.
Notice that nonlinear constraints are not supported. Therefore the following non-linear constraints cannot work:
a^2 > c;a * b > 3;1 / b > c + 3;sin(a) < c;
Bounds can be set to limit the values of the fitting parameters. When both bounds and linear constraints are used, the latter have higher priority.
Extended Notation
General linear constraint notation was extended in Origin 8.1 SR3 so that special cases are supported. These notations are useful in replica fittings for that it can represent a parameter "family".
Notation for Initial Values of Parameters
Use (i) to refer to the initial value of a parameter. For example, xc__2(i) means the initial value of the parameter xc__2. Therefore, to limit the parameter value of xc__2 so that it will not deviate from its initial value by more than 0.3, use the following constraint:
xc__2(i)-xc__2 <= 0.3;
xc__2-xc__2(i) <= 0.3;
Notation for Parameter Family
Use (a) to represent all the parameters of a family. Suppose you want all the amplitudes (A) to be less than 1, use the following constraint:
A(a) < 1;
Notation for All Parameters except a Specific One
Use (e) to indicate all parameters of a family, except the one preceding (e). The following example can ensure that the amplitude A__3 is at least twice as large as all the other amplitudes:
A__3 >= 2*A__3(e);
Note that there should not be more than one (e) in one constraint. Also, in one General Linear Constraint dialog, there should not be both (a) and (e).
Combination of Special Characters
The (e) and (a) syntax can be used with the (i) syntax. The following constraint will ensure that no peak centers will deviate from its initial value by more than 0.2
xc(ia) - xc(a) <= 0.2;
xc(a) - xc(ia) <= 0.2;
Using replica/set index
Use (n) to represent a serial of parameter family. For example, if the following is desired:
w > w__2;
w__2 > w__3;
w__3 > w__4;
w__4 > w__5;
we can use the following constraint:
w(n) > w(n+1), n=1..5;
Another example:
w(2*n-1) < w(2*n), n=1..10;
This is equivalent to:
w < w__2; w__3 < w__4; w__5 < w__6; w__7 < w__8; w__9 < w__10;
|