18.12.1 Continuous Wavelet TransformContinuous-WaveTrans
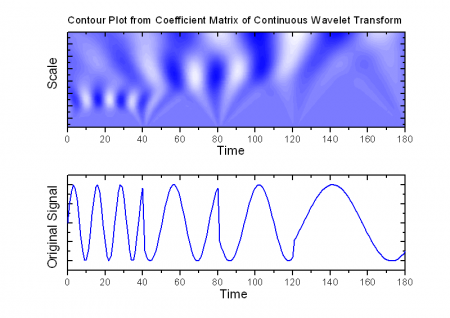
This function computes the real continuous wavelet coefficient for each given scale presented in the Scale vector and each position b from 1 to n, where n is the size of the input signal.
Let x(t) be the input signal and ψ be the chosen wavelet function, the continuous wavelet coefficient of x(t) at scale a and position b is:
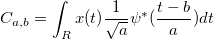
The result can be output to a range on a worksheet and, if you select the Coefficient Matrix checkbox, a matrix. The output range on the worksheet is comprised of m columns, each of which has n rows, where m is the size of the Scale vector. Each column corresponds to a scale and each row corresponds to a position. On the other hand, the result matrix, if you choose to generate one, will have n columns and m rows. The value at a cell whose row number is  and column number is and column number is  is the coefficient of scale is the coefficient of scale 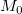 and position and position 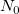 . .
Now three types of wavelet are supported in this function, including Morlet, Mexican Hat, and the Derivative of Gaussian wavelets.
The Morlet wavelet is defined as:

where k is the wave number.
The Mexican Hat wavelet is:
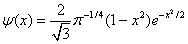
And the Gaussian wavelet is the pth derivative of the Gaussian function, which is defined as:

where p is the derivative order.
To Perform Continuous Wavelet Transform
- Make a workbook or a graph active.
- Select Analysis: Signal Processing: Wavelet: Continuous Wavelet from the Origin menu.
|
Topics covered in this section:
|
|