2.19.1 LabTalk-Supported FunctionsLT-Supported-Functions
String Functions
| Note: All of the following functions are available only in the Origin 8 SR6 or later version!
|
| Name
|
Brief Description
|
| Between(str$, str1$, str2$)$
|
Extracts string or characters between str1$ and str2$ in str$. examples:
-
Between([Results]"March 2009"!"Average Return"[1:31],"!","[")$ returns "Average Return".
|
| Char(number)$
|
Takes an integer 1-255, returns the ASCII character. examples:
-
char(65)$ returns A.
-
char(col(B))$ returns ASCII characters corresponding to integer values in col(B).
|
| Code(str$)
|
Takes a string, returns ASCII code for the first character. examples:
-
str$ = "abc"; code(str$) returns 97.
-
code(col(D)) returns integers corresponding to the ASCII code for the first character in the string in col(D).
|
| Compare(str1$, str2$ [,Case])
|
Takes two strings, returns 1 (identical) or 0 (not identical). Option Case controls case sensitivity: 1 = true (default), 0 = false. examples:
-
str1$ = "ABC"; str2$ = "abc"; compare(str1$,str2$,0) returns 1.
-
compare(col(F), col(G),1) returns "0" when string or case does not match, or "1" when string and case do match.
|
| CompareNoCase(str$, str2$)
|
Takes two strings, returns 0 (identical), -1 ( str$ is less than str2$ in the alphabetical order), or 1(str$ is greater than str2$). examples:
-
str1$ = "ABC"; str2$ = "abc"; comparenocase(str1$,str2$) returns 0.
-
comparenocase("ijk","ab") returns 1
-
comparenocase("ijk","xyz") returns -1
|
| EnvVar(variableName$)
|
Takes a string, returns the string value stored in the corresponding Windows environment variable. if this string is not a valid Windows environment variable string, missing will be returned. examples:
-
EnvVar("appdata")$ returns the directory path to the Application Data folder.
|
| Exact(str1$, str2$)
|
Takes two strings, returns 1 (identical, including case) or 0 (not identical). examples:
-
str1$ = "ABC"; str2$ = "abc"; exact(str1$,str2$) returns 0.
-
exact(col(F), col(G)) returns "0" if not an exact string match or "1" if exact match (incl. case).
|
| Find(within$,find$[,StartPos])
|
Searches within$ for find$, returns the position from the first character in within$ (found) or -1 (not found). Option StartPos controls start search position (default = 1). Case sensitive. No wildcards. examples:
-
str1$ = "abcde"; str2$ = "bc"; find(str1$,str2$) returns 2.
-
find(col(G),col(J)) searches the col(G) string for the col(J) string, starting from the first character; if found, returns the position of the col(J) string, in the col(G) string.
|
| FindOneOf(within$,find$)
|
Searches find$ for the first character that is found in within$, if found, returns the 1-base index of the first found character. Case sensitive. No wildcards. examples:
-
str1$ = "abcde"; str2$ = "xb"; findOneOf(str1$,str2$) returns 2.
|
| GetAt(str$,index)
|
Returns a single character specified by index in str$. examples:
-
str$ = "sss abc"; GetAt(str1$,5) returns 97.
|
| GetFileExt(strFile$)$
|
Get the file extension from the full path strFile$. examples:
-
GetFileExt("origin.ini")$ returns "ini".
|
| GetFileName(strFile$,bRemoveExt)$
|
Get the file name ( without extension if bRemoveExt = 1) from the full path strFile$. examples:
-
GetFileName("%Yorigin.ini")$ returns "origin.ini".
|
| GetFilePath(strFile$)$
|
Get the path from the full path strFile$. examples:
-
GetFilePath("%Yorigin.ini")$ returns the path string.
|
| GetLength(str$)
|
Get the length of a str$. examples:
-
GetLength("origin.ini")$ returns 10.
|
| GetToken(str$,n,chDelimiter)$
|
Returns the nth token where a token is separated by chDelimiter. examples:
-
GetToken("sss|abc|def|xyz", 3,"|")$ returns "def".
|
| IsEmpty(str$)
|
Similar to MS Excel's ISBLANK function. Used to determine whether a worksheet cell is empty or not. Argument str can be a cell address or a column of values. example:
-
isempty(col(A)[2]$)=; // return 0 if cell row 2, col 1 contains a value; or 1 if empty.
|
| IsFile(str$)
|
Test whether str is a valid full path file name example:
-
IsFile("origin.ini")=; // return 1 if the file exist.
|
| IsFormula(str$)
|
Determine whether a worksheet cell contains cell formula or not. example:
-
isformula(A2)=; // return 1 if cell row 2, col 1 contains cell formula; otherwise return 0.
|
| IsPath(str$)
|
Test whether str is a valid file path example:
|
| Left(str$, n)$
|
Takes a string str$, returns the leftmost n characters. examples:
-
str$ = "abcde"; Left(str$,3)$ returns abc.
-
left(col(G),3)$ returns the leftmost 3 characters in the col(G) string.
|
| Len(str$)
|
Takes a string str$, returns the number of characters. examples:
-
str$ = "abc ABC"; Len(str$) returns 7.
-
len(col(G)) returns the number of characters in the col(G) string.
|
| Lower(str$)$
|
Takes a string str$, converts it to lowercase. examples:
-
str1$ = "ABCDE"; str2$ = Lower(str1$)$ returns abcde.
-
lower(col(F))$ returns the strings in col(F) in lower case.
|
| MakeCSV(str$[, quote, output_delim, input_delim$])$
|
Takes a delimited string, converts it to CSV. Option quote to enclose output: 0 (default) = no quotes, 1 = single quotes, 2 = double quotes. Option output_delim: 0 = comma, 1 = semicolon. Option input_delim$ specifies source string delimiter (not needed if white space). examples:
-
str$ = "This is a test value"; MakeCSV(str$, 1, 0)$ returns 'This','is','a','test','value'.
-
makecsv(col(N),0,0)$ takes a space-separated string in col(N) and returns a string of comma-separated values.
|
| Match(within$,find$[,Case])
(2015 SR0)
|
This function compares the string find$ with another string within$ to see whether their contents match with each other. It returns 1 (True, match) or 0 (False, not match). Note that wildcard characters "*" and "?" are supported in the find$ string variable. Optionally you can use case sensitive check, the option Case controls case sensitivity: 0 (default) = false, 1 = true. examples:
-
str1$ = "From: test@Originlab.com"; str2$ = "F*com"; Match(str1$,str2$); returns 1.
|
| MatchBegin(within$,find$[,StartPos,Case])
|
Search string within$, return an integer corresponding to the start position of find$ or -1 (not found). Supports "*"' and "?" wildcards. Option StartPos specifies the position of the character at which to start the search: 1 (default) = search from 1st character. Option Case controls case sensitivity: 0 (default) = false, 1 = true. examples:
-
str1$ = "From: test@Originlab.com"; str2$ = "From*@"; MatchBegin(str1$,str2$,1); returns 1.
-
matchbegin(col(a)," ") returns the starting position of the of the first white space in col(a) or if none found, returns -1.
|
| MatchEnd(within$, find$[, StartPos, Case])
|
Search string within$, return an integer corresponding to the end position of find$ or -1 (not found). Supports "*" and "?" wildcards. Option StartPos specifies the position of the character at which to start the search: 1 (default) = search from 1st character. Option Case controls case sensitivity: 0 (default) = false, 1 = true. examples:
-
str1$ = "From: test@Originlab.com"; str2$ = "From*@"; MatchEnd(str1$,str2$,1); returns 11.
-
MatchEnd(col(A),col(B)) returns the ending position of the col(b) string in col(a) or if no match, returns -1.
|
| Mid(str$, StartPos [, n])$
|
Takes a string str$, returns n characters from StartPos or if n not specified, returns everything from StartPos. examples:
-
str$ = "aabcdef"; Mid(str$,2,3)$ returns abc.
-
str$ = "aabcdef"; Mid(str$,2)$ returns abcdef.
-
mid(col(a),1,3)$ returns the first three characters of string in col(a).
|
| NumberValue(str$ [, Decimal$, Group$])
|
Takes a string or vector of strings and returns as numeric. Option Decimal used to interpret string decimal separator. Option Group used to interpret group separator. Enclose string and options in quotes. examples:
-
numbervalue("1,000.05")=; // returns 1000.05 (US regional settings)
-
numbervalue("5.000,0", ",", ".")=; // returns 5000 (US regional settings)
|
| NumBreak(str$ [, offset, decimal])
(2026)
|
It scans a mixed string str$ from the given index offset (optional) and returns the position where the character type first switches between digit and non-digit. Optional parameter decimal determines whether to use the decimal separator in the text string opposite to current system used. If text str$ uses comma "," as the decimal separator and the current system uses period ".", set decimal to 1 to treat comma as decimal separator. Vice versa. examples:
-
numbreak("abc123")=; returns 4;
-
numbreak("Club45North", 5)=; returns 7 since it scan from "4";
-
numbreak("abcd12,343", 5, 1)=; reurns -1 since "12,343" is treated as number "12.343" and no digit and non-digit switch from "1".
|
| NumExtract(str$ [, count, decimal])$
(2026)
|
It takes a mixed string str$ and returns the count-th consecutive digit block. If count is omitted it defaults to 1 (i.e. return the first block); count = 0 returns the last block. decimal determines whether to use the decimal separator in the text string opposite to current system used. If text str$ uses comma "," as the decimal separator and the current system uses period ".", set decimal to 1 to treat comma as decimal separator. Vice versa. examples:
-
numextract("1-413-586-2013",2)$=; returns 413;
-
numextract("1-413-586-2013",0)$=; returns 2013;
-
numextract("abcd12,343", 1, 1)$=; returns 12,343 since "12,343" is treated as "12.343" rather than two numbers.
|
| Replace(within$, StartPos, n, replace$)$
|
Replace n characters in within$, starting from StartPos, with string replace$. String replace$ may differ in length from n. examples:
-
Replace(abcdefghijklmn,3,5,123456)$ returns ab123456hijklmn.
-
replace(col(a),1,4,"Replacement string ")$ replaces the first four characters in col(a) with string "Replacement string " (including spaces).
|
| Right(str$, n)$
|
Takes a string str$, returns the rightmost n characters. examples:
-
str$ = "abcde"; Right(str$,n)$ returns cde.
-
right(col(d),8) returns the rightmost 8 characters in the string in col(d).
|
| Search(within$, find$[, StartPos])
|
Returns position of string find$ within string within$, or if not found returns -1. Not case sensitive. No wildcards. Option StartPos controls where to start search (default = 1). examples:
-
within$ = "abcde"; find$ = "BC"; Search(within$,find$) returns 2.
-
search(col(c),"sample") returns the position of the word "sample" in the string in col(c).
|
| SpanExcluding(source$, strEx$)
|
Extracts and returns all characters preceding the first occurrence of a character from strEx; Case sensitive. examples:
-
str1$= "Hello World! Goodbye!"; str2$ = "ho"; SpanExcluding(str1$, str2$)$= ; returns Hell.
|
| SpanIncluding(source$, strIn$)
|
Extracts characters from the string source, starting with the first character that are in the set of characters identified by strIn; Case sensitive. examples:
-
str1$= "cabinet"; str2$ = "acB"; SpanIncluding(str1$, str2$)$= ; returns ca.
|
| Substitute(within$,sub$,find$ [, n])$
|
Search string within$ for string find$, replace with sub$. Option to substitute only the nth found instance. examples:
-
Substitute(abcdefabcdef,12,bcd,0)$ returns a12efa12ef.
-
substitute(col(c),"experiment: ","expt.",1) searches string in col(a) and substitutes "experiment: " for "expt.", replacing only the first instance found.
|
| Text(d[,fmt$])$
(9.1 SR0)
|
Converts a double to string. Option fmt$ formats output; if not specified, uses column's format settings. Use empty string "" to use @SD digits. Use "*" to use Origin's global setting. examples:
-
Text(2.01232,"*3")$ returns 2.01.
-
Text(Date(7/10/2014),D1)$ returns Thursday, July 10, 2014.
-
text(date(col(b)),D1)$ takes a column of date data and returns a string in the format of "Wednesday, March 05, 2014"
|
| Token(str$,iToken[, iDelimiter])$
|
Takes string str$, returns substring corresponding to index iToken. Option iDelimiter is ASCII value of delimiter: 0 (default) = any white space; 32 = single space; 124 = "|". Most symbol chars such as "_" (ASCII 95), "|"(ASCII 124) can be directly used as iDelimiter. examples:
-
str1$="This is my string"; Token(str1$,3)$ returns my.
-
token(col(c),2) returns the second token (as delimited by white space) in the string in col(c).
-
token(col(b), 3, ":") returns the third token as delimited by colon in the string in col(b).
Note: some symbol chars might not be directly used by iDelimiter but their ASCII values always apply.
|
| Trim(str$[, n])$
|
Takes string str$ and removes spaces. Parameter n controls how space is removed: 0 (default) = leading + trailing, 1 = remove all. examples:
-
str1$ = " abc ABC "; Trim(str1$,0)$ returns abc ABC.
-
trim(col(a),0) returns the string in col(c) with leading and trailing spaces controlled.
|
| Upper(str$)$
|
Takes string str$, returns as uppercase. examples:
-
str1$ = "abcde"; Upper(str1$)$ returns ABCDE.
-
upper(col(c))$ returns the string in col(c) in uppercase letters.
|
| Value(str$[, decimal])
|
Takes string number str$, returns it as double. Optional parameter decimal determines whether to replace the decimal separator in the text string. If text str$ uses comma "," as the decimal separator and the current system uses period "." as decimal, set decimal to 1 to replace comma with period. Vice versa. examples:
-
str$ = "+.50"; Value(str$) returns 0.5. Note: see the atof() function.
-
value(col(e)) takes a string number in col(e) and returns it as a numeric of type double.
-
value("12,3", 1) takes a string "12,3" and returns it as a number "12.3"
|
A note on the "$" notation and string functions
Note: Use of the "$" when working with strings can be confusing:
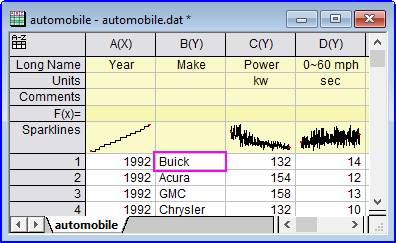
aa$=col(b)[1];
aa$=;
// returns
col(b)[1]
aa$=col(b)[1]$;
aa$=;
// returns
Buick
aa$=upper(col(b)[1]$);
aa$=;
// returns
upper(col(b)[1]$)
aa$=upper(col(b)[1]$)$;
aa$=;
// returns
BUICK
Math Functions
| Name
|
Brief Description
|
| abs(x)
|
Returns the absolute value of x. example:
-
abs(-2.5) returns 2.5; abs(0/0) returns -- (missing value);
-
abs(col(b)) returns absolute value of every element in col(b).
|
| ceil(x[, sig])
(2019 SR0)
|
Returns a value by adjusting the given value x away from 0 and to the multiple of sig nearest to x. example:
-
ceil(2.5, 2) returns 4;
-
ceil(-2.5, 2) returns -2.
|
| Combina(n,k)
(2019 SR0)
|
Given n elements, return the number of combinations of k elements with repetitions. example:
|
| Combine(n1,n2)
|
Given n1 elements, return the number of combinations of n2 elements. example:
-
combine(4,2) returns 6.
-
combine(col(a),2 returns the number of combinations of 2 elements for the value in col(a).
|
| Distance(px1, py1, px2, py2)
|
Takes the XY coordinates of two points, returns the shortest distance. examples:
-
distance(0,0,0,1) returns 1.
-
distance(col(g),col(h),col(i),col(j)) could also return 1.
|
| Distance3D(px1, py1, pz1, px2, py2, pz2)
|
Takes the XYZ coordinates of two points, returns the shortest 3D distance. examples:
-
distance3d(0,0,1,0,0,2) returns 1.
-
distance3d(col(a),col(b),col(c),col(d),col(e),col(f)) could also return 1.
|
| exp(x)
|
Returns e raised to the x power. Note: x > 667 returns missing value. examples:
-
exp(0) returns 1.
-
exp(col(a)) returns e raised to the value in col(a).
|
| expm1(x)
|
Returns the value of exp(x)-1 accurately for the small values of x. examples:
-
expm1(0.00574) returns 0.0057565053651536.
|
| fact(n)
|
Returns the factorial of a non-negative integer. Note: n > 170 returns missing value; see the Log_gamma function. examples:
-
fact(3) returns 6.
-
fact(col(a)) returns factorial of value in col(a).
|
| factdouble(n)
|
Returns the double factorial of a non-negative integer.
If n = odd, sequence is 1*3*5...(n-2)*n; if n = even, sequence is 2*4*6...(n-2)*n; if n = 0, evaluates to 1. If n > 299, returns missing value. examples:
-
factdouble(6) returns 48;
-
factdouble(col(a)) returns the double factorial of value in col(a).
|
| floor(x[, sig])
(2019 SR0)
|
Returns a value by adjusting the given value x towards 0 and to the multiple of significance nearest to x. example:
-
floor(2.5, 2) = ; returns 2;
-
floor(-2.5, -2) = ; returns -2.
|
| gcd(n1, n2[, ...])
(2019 SR0)
|
Returns the greatest common divisor of a group of given integers n1, n2, n3, etc. example:
|
| frac(x)
|
Returns the fractional part of a double.
example:
-
frac(3.1415) = ; returns 0.1415.
|
| HaversineDistance(lon1,lat1,lon2,lat2,r[,degree])
(2017 SR0)
|
Takes the longitudes and latitudes of two points on a sphere with radius r, returns the great-circle distances between them. Option degree determines whether to use degree or radian as the unit of longitudes and latitudes (default is degree). example:
-
HaversineDistance(120, 30, 0, -60, 5000) returns 11388.7402734106;
|
| int(x)
|
Takes a double x and returns the truncated integer. examples:
-
int(7.9) returns 7.
-
int(col(a)) returns the truncated integer in col(a).
|
| ln(x)
|
Return the natural logarithm of x.
|
| ln1p(x)
|
Return the natural logarithm of x when x is very close to 1.
|
| log(x)
|
Return the base 10 logarithm of x.
|
| mod(n, m)
|
Returns the integer modulus of integer n divided by integer m (quotient rounds toward 0). examples:
-
mod(16,7) returns 2.
-
mod(col(a),col(b)) returns the integer modulus of the value in col(a) divided by the value in col(b).
|
| mod2(n,m)
|
Returns the integer modulus of integer n divided by integer m (quotient rounds toward minus infinity). Quotient of  , which is used to calculate modulus, rounds toward , which is used to calculate modulus, rounds toward  . When the input(s) are negative, the return may differ from mod (it calculates quotient of . When the input(s) are negative, the return may differ from mod (it calculates quotient of  rounds toward 0). examples: rounds toward 0). examples:
-
mod(5,-3) returns -1
-
mod(col(a),col(b)) returns the integer mod2 of the value in col(a) divided by the value in col(b).
|
| nint(x)
|
Takes a double x and rounds up/down to the nearest integer. The nint(x) function returns the same result as round(x, 0).
|
| permut(n, k)
(2019 SR0)
|
Returns the number of permutations for a specified k elements from a given set of n elements. examples:
|
| prec(x, n)
|
Takes a value or a dataset, returns it with n significant figures. examples:
-
x = 1234567; prec(x, 3) returns 1230000.
-
prec(col(b), 3) assigns the values in col(b) to the target column, to 3 significant figures.
|
| product(vd)
|
Multiplies all the numbers from vd and returns the product. examples:
|
| rmod(x, y)
|
Returns the real modulus of double x divided by double y (quotient rounds toward 0). Quotient of  rounds toward rounds toward 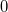 . examples: . examples:
-
rmod(4.5, 2) returns 0.5.
-
rmod(col(a),3) returns the rmod of col(a) divided by 3.
|
| rmod2(x, y)
|
Returns the real modulus of double x divided by double y (quotient rounds toward minus infinity). Quotient of  rounds toward rounds toward  . examples: . examples:
-
rmod2(-4.5, 2) returns 1.5.
-
rmod(col(a),3) returns the rmod2 of col(a) divided by 3.
|
| round(x, n)
|
Takes a value or dataset, returns the value or dataset to n decimal places. Note: Origin 9.1 introduced a new rounding algorithm. System variable @RNA toggles between old and new methods (old behavior is @RNA=0; new behavior is @RNA=1 (default)). examples:
-
round(1.156, 1) returns 1.2.
-
round(col(a),2) returns the values in col(a), rounded to 2 decimal places.
|
| sign(x)
|
Takes a real number x and returns its sign. If x > 0, returns 1; If x < 0, returns -1; If x = 0, returns 0.
|
| sqrt(x)
|
Takes a double x and returns the square root.
|
| Derivative(vd[,n])
|
Takes a vector vd, returns the derivative of the data list. No smoothing is performed. Option n is derivative order (default = 1).
|
| DerivativeXY(vx, vy [, n])
|
Takes two vectors vx and vy, returns the derivative of the curve. Option n is derivative order (default = 1).
|
| Integral(integrand,lowerlimit,upperlimit[, arg1, arg2, ...])
|
Perform one dimension integration value, and returns the integral value.
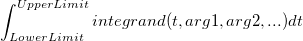
|
| Integrate(vd)
|
Integrate the area under a curve. Uses the Trapezoid Rule.
|
| IntegrateXY(vx, vy)
|
Integrate the area under curve (vx, vy). Vector vx contains x coordinates of curve; vy contains y coordinates.
|
| Interp(x,vX,vY[,method,bound,smooth,extrap])
(2015 SR0)
|
Takes x coordinates vx and y coordinates vy and interpolates/extrapolates a y coordinate at a given coordinate x. Option method = 0 (linear, default), 1 (cubic spline), 2 (cubic B-spline), 3 (Akima spline). When method = 1, bound can equal 0 (natural) or 1 (not-a-knot). When method = 2, smooth = non-negative value for smoothness. Option extrap can be applied when X values are outside reference range: 0 (default) = extrapolate Y using last two points; 1 = set all Y as missing values; 2 = use the Y value of the closest input X.
|
| permutationa(n, k)
(2019 SR0)
|
Returns the number of permutations (with repetitions) for a specified k elements from a given set of n elements. examples:
-
permutationa(4, 2) returns 16
|
Special Math Functions
| Name
|
Brief Description
|
| beta(a, b)
|
Beta Function with parameters a and b.
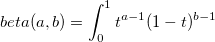
|
| incbeta(x, a, b)
|
Incomplete Beta Function with parameters x, a, b.
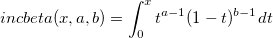
|
| incf(x, m, n)
|
The incomplete F-table function. Parameter x is the upper limit of integration; parameter m is the degrees of freedom of the numerator variance; parameter n is the degrees of freedom of the denominator variance.
|
| incgamma(a,x)
|
Compute Incomplete Gamma function at x, with parameter a.
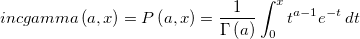
where 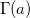 is the value of Gamma function at a. a > 0 and x ≥ 0. is the value of Gamma function at a. a > 0 and x ≥ 0.
|
| inverf(x)
|
Computes the inverse error function at x.
|
| j0(x)
|
Zero Order Bessel Function.
|
| j1(x)
|
First Order Bessel Function.
|
| jn(x, n)
|
Bessel function of order n.
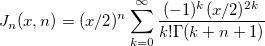
where 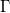 is the gammaln(x) function. is the gammaln(x) function.
|
| y0(x)
|
Zero order Bessel function of second kind.
|
| y1(x)
|
First order Bessel function of second kind.
|
| yn(x, n)
|
nth order Bessel function of second kind.
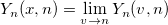
where
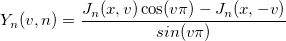
|
Trigonometric/Hyperbolic Functions
| Note: Angular units (radians, degrees, gradians) depend upon system.math.angularunits property (also set in Preference: Options: Numeric Format).
|
| Name
|
Brief Description
|
| acos(x)
|
Returns the arccosine of x. If x < -1 or x > 1, missing value ("--") is returned.
|
| acosh(x)
|
Returns the inverse hyperbolic cosine of x. If x is < 1, missing value ("--") is returned.
|
| acot(x)
|
Returns the arccotangent of x. Input x can be any value. Values are returned in the first or second quadrants.
|
| acoth(x)
|
Returns the inverse hyperbolic cotangent of |x| > 1.
|
| acsc(x)
|
Returns the arccosecant of |x|. If |x| is < 1, returns missing value ("--"). Values are returned in the first or fourth quadrants.
|
| acsch(x)
|
Returns the inverse hyperbolic cosecant of x. If x = 0 or x > ~3E153, returns missing value ("--").
|
| angle(x, y)
|
Returns the angle (radians), measured between the positive X axis and the line joining a point (x,y) and the origin (0,0).
|
| Angleint1(px1, py1, px2, py2 [, unit, direction])
|
Takes two pairs of x,y coordinates, returns the angle between the line defined by the two points and the X axis. Option unit: 0 = radians default) or 1 (degrees); Option direction: 0 (default) constrains the returned angular value to the first (+x,+y) and fourth (+x,-y) quadrants; or 1, returns values from 0–2pi radians or 0–360 degrees. examples:
-
angleint1(1,1,3,3,1) returns 45.
-
angleint1(col(a),col(b),col(c),col(d),1,1) returns the angle in degrees (0 - 360) between the line defined by two pairs of xy coordinates and the X axis.
|
| Angleint2(px1, py1, px2, py2, px3, py3, px4, py4 [, unit, direction])
|
Returns the angle between two lines, one with endpoints (px1, py1) and (px2, py2), the other with endpoints (px3, py3) and (px4, py4). If option unit = 0 (default), returns radians; if unit = 1 returns degrees. Option direction specifies direction of return value. If option direction = 0 (default), constrains the returned angular value to the first (+x,+y) and fourth (+x,-y) quadrants; if direction = 1, returns values from 0–2pi radians or 0–360 degrees. examples:
-
angleint2(0,0,1,0,0,1,0,0,1,1) returns 90.
-
angleint2(col(a),col(b),col(c),col(d),col(e),col(f),col(g),col(h),1,1) returns the angle (degrees, 0 - 360) between two lines defined by endpoints in col(a) - col(h).
|
| asec(x)
|
Returns the arcsecant of x. If |x| is < 1, returns missing value ("--"). Values are returned in the first or second quadrant.
|
| asech(x)
|
Returns the inverse hyperbolic secant of x. 0 < x ≤ 1. Other values of x return a missing value ("--").
|
| asin(x)
|
Returns the arcsine of x. -1 ≤ x ≤ 1. Other values of x return a missing value ("--").
|
| asinh(x)
|
Returns the inverse hyperbolic sine of x (any real number).
|
| atan(x)
|
Returns the arctangent of x (any real number).
|
| atan2(y,x)
|
Takes coordinates x,y (doubles), returns the angle between the positive X axis and the point (x,y). A variation of the atan(x) function. Returns value between -π and π. Angle is (+) for counter-clockwise angles (y > 0) and (-) for clockwise angles (y < 0).
|
| atanh(x)
|
Returns the inverse hyperbolic tangent of x. -1 < x < 1. Other values of x return a missing value ("--").
|
| cos(x)
|
Returns the cosine of x.
|
| cosh(x)
|
Returns the hyperbolic cosine of x.
|
| cot(x)
|
Returns the cotangent of x.
|
| coth(x)
|
Returns the hyperbolic cotangent of x. Value x is any non-zero number. Note that numbers of absolute value > 710 (approx.) return a missing value ("--").
|
| csc(x)
|
Returns the cosecant of x. If x = 0, returns missing value ("--").
|
| csch(x)
|
Returns the hyperbolic cosecant of x. Value x is any non-zero number. Note: when x > 710 (approx.), returns a missing value ("--").
|
| Degrees(angle)
|
Takes angle in radians and returns degrees.
|
| Radians(angle)
|
Takes angle in degrees and returns radians.
|
| secant(x)
|
Returns the secant of x. Note: Do not confuse with the sec() function which returns the seconds value of a date.
|
| sech(x)
|
Returns the hyperbolic secant of x. Note that numbers of absolute value > 710 (approx.) return a missing value ("--").
|
| sin(x)
|
Returns the sine of x.
|
| sinh(x)
|
Returns the hyperbolic sine of x.
|
| tan(x)
|
Returns the tangent of x.
|
| tanh(x)
|
Returns the hyperbolic tangent of x.
|
Date and Time Functions
Note: Beginning with Origin 2019, there are three date-time systems in Origin. The default system remains the long-time, adjusted Julian Date system as explained in Dates and Times in Origin. The examples in the table below assume the long-time, default date-time system and when you see "Julian-date value", this refers to Origin's adjusted date value. These following functions should work with the alternate systems ...
date2str(today(), "MM/dd/yyyy")$ = 09/27/2018 // default date-time system
date2str(today(), "MM/dd/yyyy")$ = 09/27/2018 // "2018" system, @DSP=2018
... but keep in mind that the numeric values that equate to a given calendar date will differ between systems:
date(9/27/2018) = 2458388 // default date-time system
date(9/27/2018) = 269 // "2018" system, @DSP=2018
For information on Origin's alternate date-time schemes, see Alternate Date-Time Systems in Origin.
| Name
|
Brief Description
|
| AddDay(vv)
(2021)
|
Takes a time vector vv and returns the day-added data when hours wrap after 24. examples:
-
addday(col(A)) adds day information to time data in col(A) and returns date and time data .
|
| Date(MM/dd/yyHH:mm:ss.##[,format$])
|
Takes a date-time string and returns Julian-date value. If format$ is not specified, string is interpreted using system short date format. Can take values 1 = default (MM/dd/yyyy) , 2 (dd/MM/yyyy) or 3 (yyyy/MM/dd) to control format for date portion of first argument, without specifying format$ string. examples:
-
date(24-09-2009,"dd-MM-yyyy") returns 2455098.
-
date(3/5/14) returns 2456721 (US) but date(5/3/14) returns 2456721 (UK).
-
date(2/1/1986 13:13, 2) returns 2446432.5506944 but date(2/1/1986 13:13, 1) returns 2446462.5506944.
-
date(col(a)) returns a Julian-date value for the date-time string in col(a).
|
| Date(yy,MM,dd)
|
Takes doubles yy as year, MM as month, dd as day and returns the Julian-date value. examples:
-
date(20,8,31) returns 2459092.
|
| Date2str(d,format$)$
|
Takes a Julian-date value and returns a date string. examples:
-
date2str(2456573.123, "dd/MM/yyyy HH:mm")$ returns 08/10/2013 02:57).
-
date2str(col(b), "dd/MM/yyyy HH:mm")$ returns a date string in the format "dd/MM/yyyy HH:mm".
|
| DateDif(start_date,end_date,unit$)
(2026)
|
Takes 2 Julian-date value (double) start_date and end_date, returns the number of days, months, or years between these two dates, determined by unit$. examples:
-
datedif(date(1/1/2001),date(1/1/2003),"Y")=; returns 2.
|
| DatePart(datepart$, d [, n])
(2016 SR1)
|
Takes a Julian-date value (double) d and returns a portion of the date specified by datepart$, as a double. Option n specifies start of week for datepart$ = w or ww. examples:
-
datepart("yyyy", 2457360.5107885) returns 2015.
-
datepart("yyyy", A) returns the year portion of the date-time data in column A.
-
datepart("y", Today())=; returns the day number of the current year (e.g. if today() = 2457363 = 12/7/2015 = 341).
-
datepart("w", 2457360.5107885, 1)=; returns 6 but datepart(w, 2457360.5107885)=; returns 5.
|
| Day(d[,n])
|
Takes a Julian-date value, returns the day number. If option n = 1, returns 1 to 31 (month); if n = 2, returns 1 to 366 (year). examples:
- (
Day(2454827.5982639, 2) returns 362.
-
day(col(b),1) takes a Julian-date value and returns the day of the month.
|
| Hour(d)
|
Takes a Julian-date value, returns the hour as an integer. Returns 0 to 23 (0 = 12:00 A.M., 23 = 11:00 P.M.). examples:
-
Hour(0.6997854) returns 16.
-
hour(col(b)) returns the hour from Julian-date value in col(b).
|
| Minute(d)
|
Takes a Julian-date value, returns the minutes as an integer (0 to 59). examples:
-
Minute(2454827.5982639) returns 21.
-
minute(col(b)) returns the minute from the Julian-date value in col(b).
|
| Month(d)
|
Takes a Julian-date value, returns the month as an integer (0 to 12). examples:
-
month(2454821) returns 12.
-
month(col(b) returns the month of the Julian-date value in col(b).
|
| MonthName(d[,n])$
|
Takes a Julian-date value, returns the month name. Month format specified by option n: 1 = single character; 3(default) = 3 characters; 0 = full month name; -1 = 3 character English regardless of language settings. examples:
-
MonthName(2454827.5982639, 0)$ returns December.
-
monthname(col(b),0)$ returns the full month name for Julian-date values in col(b).
|
| Now()
|
Returns the current date-time as a Julian-date value. examples:
-
time2str(now()-date(col(a)),"HH:mm")$ returns a time string (HH:mm) elapsed between current time and the date string in col(a).
|
| Quarter(d)
|
Takes a Julian-date value, returns a quarter of the year. examples:
-
Quarter(2454829.5745718) returns 4.
-
quarter(col(b)) returns the quarter of the Julian-date value in col(b).
|
| Second(d[,n])
|
Takes a Julian-date value or real number, returns the seconds as a real value in the range 0 to 59.9999. Option n = 0 displays more than 3 decimal digits but the precision of Julian date values is limited to 0.0001 seconds when rounded at the fourth decimal digit. examples:
-
second(2454827.5982639) returns 30.001.
-
second(2454827.5982639, 0) returns 30.000942349434.
-
second(A) returns the seconds of Julian dates in col(a).
|
| Time(HH,mm,ss) and Time(HH:mm:ss[,Format$])
|
Takes either HH,mm,ss or custom date-time string (HH:mm:ss = default) and returns the Julian-date value. Optional Format$ argument specifies custom string format. examples:
-
time(20:50:25) returns 0.8683449; time("2 20,50,25", "DDD hh,mm,ss") returns 2.8683449.
-
time(col(a)) returns Julian-date values for time data formatted as HH:mm:ss in col(a).
|
| Time2str(d,format$)$
|
Takes a Julian-date value, returns a time string of a specified format. examples:
-
time2str(0.1875, "HH:mm")$ returns 04:30.
-
time2str(col(b),"DDD:HH")$ returns a time string formatted as DDD:HH.
|
| Today()
|
Returns the current date as a Julian-date value.
|
| UnixTime(d1[, d2, n])
(2021)
|
Convert between Unix timestamp values and Julian-date values. If optional parameter n = 0 (default), convert d1 (Unix timestamp) to Julian-date; if n = 1, convert d1 (Julian-date) to Unix timestamp. Optional parameter d2 is timezone offset. Note that when converting Julian-date to to Unix timestamp, you must specify both optional parameters (if no offset, d2 = 0). Unix timestamp units = seconds. examples:
-
unixtime(0) returns an adjusted Julian-date value of 2440587.
-
unixtime(2459011.27604,0,1) returns a Unix timestamp of 1591857450.
|
| WeekDay(d[,n])
|
Takes a Julian-date value, returns the day of the week. Option n specifies week start and end values: 0 (default) = Sunday (0-6), 1 = Sunday (1-7), 2 = Monday (0-6), or 3 = Monday (1-7). examples:
-
weekday(2454825, 1) returns 5.
-
weekday(col(b)) takes Julian-date values in col(b) and returns the day of the week as a number.
|
| WeekDayName(d[,n1,n2])$
|
Takes a Julian-date value (including time) or number defined by n2, returns the weekday. Option n1 controls output string length: -1 = 3 char cap; 0 = full name, 1st cap; 1 = 1 char cap; 3(default)= 3 char, 1st cap. Option n2 controls week start and end values: 0 = 0(Sun) - 6(Sat); 1 = 1(Sun) - 7 (Sat); 2 = 0(Mon) - 6(Sun); 3(default) = 1(Mon) - 7(Sat). examples:
-
WeekDayName(2454825,-1,0)$ returns THU.
-
weekdayname(col(b),3,0)$ returns the day of the week name, formatted as 3 char, 1st letter cap.
|
| WeekNum(d[,n1,n2])
|
Takes a Julian-date value, returns the calendar week number of the year (1 to 53). Option n1 to specify week start (Sunday vs Monday) and n2 first week of year. examples:
-
weeknum(date(1/11/2009)) returns 3.
-
weeknum(date(col(c))) takes a column of date data formatted as "MM/dd/yyyy" (col(c)), interprets it as a Julian-date value using the date() function and then returns a week number using the weeknum() function.
|
| Year(d)
|
Takes a Julian-date value, returns the year as an integer(0100-9999). examples:
-
year(2454821) returns 2008.
-
year(date(col(c))) takes a column of date data formatted as "MM/dd/yyyy" (col(c)), interprets it as a Julian-date value using the date() function and then returns the four-digit year.
|
| YearName(d[,n])$
|
Takes a Julian-date value, returns year as a string. Form of string is specified by option n: 0 = 2 digits, 1(default) = 2 digits preceded by an apostrophe, or 2 = 4 digits. examples:
-
YearName(2454827.5982639, 1)$ returns '08.
-
yearName(date(col(c)),0)$ takes a column of date data formatted as "MM/dd/yyyy" (col(c)), interprets it as a Julian-date value using the date() function and then returns the two-digit year.
|
Logical Functions
| Name
|
Brief Description
|
| if(con,val_true[,val_false])[$]
(2019 SR0)
|
Evaluate conditional expression con and returns val_true if the comparison is TRUE, val_false if FALSE. Example
-
if(A>B,1,0) will return 1 if col(A)>col(B), otherwise return 0.
-
if(A$==B$,1,0) will return 1 if string in col(A) matches string in col(B), otherwise returns 0.
-
if(A==1,100," ") will return 100 if col(A)[i]=1, otherwise leave cell blank.
|
| ifs(con1,val1[,con2,val2,]...[,con40,val40])[$]
(2019 SR0)
|
Evaluate multiple conditions conn and returns the corresponding d/str of the first TRUE condition. Example
Ifs(A>0.5,"Large",A<0.3,"Small",1,"Other")$, if values in col(A) is larger than 0.5, return Large, if smaller than 0.3, returns Small, the rest in between will return Other.
|
| ifna(val,val_na)[$]
(2019 SR0)
|
Calculate the given value val and return the specified string/numeric val_na if the result is missing, otherwise return the string display of val/numeric value val. Example
-
IfNA(col(A)/col(B),"not found")$, return "not found" if col(A)/col(B) is missing, otherwise return the string display of col(A)/col(B)
|
| switch(expression,val1,res1[,val2,res2]...[,val39,res39][,default])[$]
(2019 SR0)
|
Evaluate value expression with a set of values val,and if there is a matched value valn, return the corresponding resn. Example
-
switch(A,1,"A1",2,"B1",3,"C1","Other")$
|
Signal Processing Functions
| Name
|
Brief Description
|
| fftamp(cx [,side])
(2015 SR1)
|
Takes a complex vector cx (usually FFT complex result), returns the amplitude. Option side defines the output spectrum (1 = one-sided, 2 = two sided and shift). examples:
-
fftamp(fftc(col(B)), 2) returns the amplitude of the FFT complex result(two-sided) of input signal in column B.
-
col(C) = col(B)-mean(col(B)); fftamp(fftc(col(C))) returns the amplitude result with DC offset removed (one-sided).
|
| fftc(cx)
(2015 SR1)
|
Takes a vector cx, returns the complex FFT result. Note that the data type of output column needs to be set as complex (16) in advance. examples:
-
fftc(col(B)) returns the FFT complex result of input signal in column B
-
fftc(rSignal) returns the FFT complex result of input signal in range variable rSignal
|
| fftfreq(time, n[, side , shift])
(2015 SR1)
|
Takes the sampling interval time and signal size n, returns the frequencies for the FFT result. Option side defines the output spectrum (1 = one-sided, 2 = two sided), shift defines whether to shift for two-sided. ( 0 = no shift, 1 = shift).examples:
-
fftfreq(0.001, 100) returns a dataset that starts from 0 to 500 with interval 10 (one-sided, no shift)
-
fftfreq(0.01, 100, 2, 1) returns the two-sided and shifted frequency for sampling interval 0.01.
|
| fftmag(cx [,side])
(2015 SR1)
|
Takes a complex vector cx (usually FFT complex result), returns the magnitude. Option side defines the output spectrum (1 = one-sided, 2 = two sided and shift).examples:
-
fftmag(fftc(col(B)), 2) returns the magnitude of the FFT complex result(two-sided) of input signal in column B.
-
col(C) = col(B)-mean(col(B)); fftmag(fftc(col(C))) returns the magnitude result with DC offset removed (one-sided).
|
| fftphase(cx[, side, unwrap, unit])
(2015 SR1)
|
Takes a complex vector cx (usually FFT complex result), returns the phase. Option side defines the output spectrum (1 = one-sided, 2 = two sided and shift), unwrap defines whether to unwrap phase angle (0 = wrap, 1 = unwrap), unit defines the unit (0 = radians, 1 = degrees).examples:
-
fftphase(fftc(col(B))) returns the phase of the FFT complex result (one-sided, unwrapped, in degrees) of input signal in column B
-
fftphase(fftc(col(B)), 2, 0, 0) returns the phase of the FFT complex result (two-sided, wrapped, in radians) of input signal in column B
|
| fftshift(cx)
(2015 SR1)
|
Takes a complex vector cx (usually FFT complex result or frequency), returns a shifted vector. Note that the data type of output column needs to be set as complex (16) in advance.examples:
-
fftshift(fftc(col(B))) returns a shifted complex vector
|
| ifftshift(cx)
(2015 SR1)
|
Takes a complex vector cx (usually shifted FFT result), returns an unshifted vector. Note that the data type of output column needs to be set as complex (16) in advance.examples:
-
ifftshift(col(B)) returns an unshifted vector, in which column B contains a complex vector with shift.
|
| invfft(cx)
(2015 SR1)
|
Takes a complex vector cx (usually FFT complex result), returns the inverse FFT result. Note that the data type of output column needs to be set as complex (16) in advance.examples:
-
invfft(ifftshift(col(B))) returns the inverse FFT result for shifted FFT complex result in column B.
|
| windata(type, n)
(2015 SR1)
|
Takes integers of type(window type) and n(window size), returns the window signal as a vector of size n.example:
-
windata(2, 50) returns the triangular window signal with vector size 50
|
Basic Statistical Function
| Name
|
Brief Description
|
| Average(vd)
(2026)
|
Takes a vector vd, returns the average. It works exactly the same as Mean(vd). example:
-
average(A) returns the average value of col(A).
Note: To calculate the average of multiple datasets by row, you can use syntax sum(vd)_average.
-
sum(A:D)_average to calculate the average from col(A) to col(D) by row
See sum(vd) function for more information.
|
| Count(vd[,n])
|
Takes a vector vd, returns the number of elements. Option n specifies element: 0 (default) = all; 1 = numeric; 2 = missing; 3 = exclude missing. example:
-
count(col(a),2) might return 22 for number of missing values.
-
count(col(a),3) might return 155 for number of values - missing values.
|
| Max(vd)
|
Takes a vector vd, returns the maximum value. example:
-
max(col(A)) returns max value in col(A).
-
max(1,2,3,4,9) returns 9.
|
| Mean(vd)
|
Takes a vector vd, returns the average. It works exactly the same as Average(vd). example:
-
mean(col(A)) returns the average value of col(A).
Note: If you want to calculate the average of multiple datasets by row, you can use syntax sum(vd)_mean.
-
sum(A:D)_mean to calculate the mean from col(A) to col(D) by row
See sum(vd) function for more information.
|
| Median(vd[,method])
|
Takes a vector vd, returns the median. Option method specifies the interpolation method: 0 (default) = empirical distribution with averaging; 1 = nearest neighbor; 2 = empirical distribution; 3 = weighted average right; 4 = weighted average left; 5 = Tukey hinge). example:
-
median(col(A),2) returns the median (as determined using method = 2). For more on interpolation methods, see Interpolation of Quantiles.
|
| Min(vd)
|
Takes a vector vd, returns the minimum value.
|
| Ss(vd [,ref])
|
Takes a vector vd, returns the sum of squares. Sum of squares is calculated after subtracting some reference value ref from each value in vd. Option ref defaults to the mean of vd but ref can be a constant, a dataset or a function. example:
-
ss(vd) returns the mean-subtracted sum of squares.
-
ss(vd,4) returns the sum of squares, calculated after subtracting 4 from each member of vd.
-
ss(vd1,vd2) returns the sum of squares, calculated after subtracting each member of vd2 from the corresponding member of vd1.
-
AA = 1; BB = 2; ss(vd, AA+BB*x) returns the sum of squares, calculated after subtracting the line described by 1+2x from vd.
|
| StdDev(vd)
|
Takes a vector vd, returns the sample standard deviation. It works exactly the same as StDev.s(vd)example:
-
StdDev(col(A)) returns sample standard deviation.
|
| StDev.s(vd)
(2026)
|
Takes a vector vd, returns the sample standard deviation. It works exactly the same as StdDev(vd). example:
-
StDev.s(A) returns sample standard deviation of col(A).
|
| StdDevP(vd)
|
Takes a vector vd, returns the population standard deviation. It works exactly the same as StDev.p(vd)example:
-
StdDevP(col(A)) returns population standard deviation.
|
| StDev.p(vd)
(2026)
|
Takes a vector vd, returns the population standard deviation. It works exactly the same as StdDevP(vd). example:
-
StdDevP.p(A) returns population standard deviation of col(A)..
|
| Sem(vd)
(2020b)
|
Takes a vector vd, returns the standard error. example:
-
Sem(col(A)) returns standard error.
|
| Total(vd)
|
Takes a vector vd, returns the sum of elements. example:
-
total(col(a)) returns the sum of all data points in column A.
|
| averageif(vd, con$)
|
Takes a vector vd and a conditional con$ and returns the mean of values satisfying con$. example:
-
col(A) = data(1,32); con$ = col(A) > 5 && col(A) < 10; averageif(col(A), con$)=; returns 7.5.
|
| Countif(vd,con$)
|
Takes a vector vd, returns the count of values satisfying condition con$. Condition con$ should be enclosed by double-quotes (" ").
-
countif(col(b),"col(b)>0")=;
-
countif(col(A),"col(A)<10 && col(A)>5")=;
|
| Maxifs(vd,con$)
|
Takes vector vd, returns the maximum values satisfying condition con. Example
-
maxifs(col(A), "col(A)>5") returns the maximum in the sub-set of col(A) larger than 5.
|
| Minifs(vd,con$)
|
Takes vector vd, returns the minimum values satisfying condition con. Example
-
minifs(col(A), "col(A)>5") returns the minimum in the sub-set of col(A) larger than 5.
|
| sumif(vd,con$)
|
Takes a vector vd, returns sum of values satisfying condition con$.
|
| sumproduct(vd1[,vd2,...])
(2026)
|
Multiplies the corresponding elements in the given datasets vd1, vd2,... and returns the grand total. The datasets are separated by comma by default, and can be replaced by another operator symbol (+, –, /) to add, subtract or divide. example:
sumproduct(A1:A3, B6:B8, C11:C13) calculates A1*B6*C11+A2*B7*C12+A3*B8*C13
|
Statistical Functions
| Name
|
Brief Description
|
| Correl(vx, vy)
|
Takes datasets vx and vy, returns the correlation coefficient. example:
-
for(ii=1;ii<=30;ii++) col(1)[ii] = ii; col(2)=ln(col(1)); correl(col(A),col(B))=; returns 0.92064574677971.
|
| cov(vx, vy[, avex, avey])
|
Takes datasets vx and vy and respective means avex and avey, returns the covariance. example:
-
for(ii=1;ii<=30;ii++) col(1)[ii] = ii; col(2)=ln(col(1)); cov(col(A),col(B))=; returns 6.8926313172818.
|
| Forecast(x,vx,vy)
|
Takes x coordinates vx and y coordinates vy and performs linear regression to calculate or predict y coordinate at given coordinate x.
|
| Intercept(vx,vy)
|
Takes two vectors, vx (independent) and vy (dependent), returns the intercept of the linear regression.
|
| mae(vobs,vpred)
(2023b)
|
Takes two vector, vobs(observation) and vpred (prediction), returns the mean absolute error.
|
| mbe(vobs,vpred)
(2023b)
|
Takes two vector, vobs(observation) and vpred (prediction), returns the mean bias error.
|
| rms(vd)
|
Takes a vector vd, returns the root mean square.
|
| rmse(vobs,vpred)
(2023b)
|
Takes two vector, vobs(observation) and vpred (prediction), returns the root mean square error.
|
| Slope(vx,vy)
|
Takes two vectors, vx (independent) and vy (dependent), returns the slope of the linear regression.
|
| ave(vd, size[, stats])
|
Takes a vector vd, returns a range of averages of each group of size. stats prodives option to output other statistics qualities rather than average. If elements of vd is not an even multiple of size, then the returned average will represent only mod(vdSize,size) elements. example:
-
ave(col(a),5) breaks col(a) into groups of size 5 and calculates an average for each group.
-
ave(A,5,2) breaks col(a) into groups of size 5 and calculates SD for each group
|
| diff(vd[,n])
|
Takes a vector vd, returns a range of differences between adjacent elements. The first element in the returned range is vd(i+1)-vdi, and so forth. Returns N-1, N, or N+1 elements, depending on value of optional parameter n:
- 0 = (default), returns N-1 elements;
- 1 = pad with 0 at dataset end, return N elements;
- 2 = pad wth 0 at dataset begin, return N elements;
- 3 = pad with 0 at dataset begin, return N+1 elements where element N+1 is obtained by totaling N elements;
- 4 = pad with NANUM at dataset begin, return N elements.
|
| sum(vd)
|
The sum() function has two modes:
In "column" mode, it takes a vector vd of single column and returns a vector which holds the values of the cumulative sum (from 1 to i, i=1,2,...,N). Its i+1th element is the sum of the first i elements. The last element of the returned range is the sum of all elements in the dataset. example:
In "row" mode, it takes two or more columns and returns a vector of row-wise sums. Syntax suffix _mean, _sd, _median, _max, _min, _n can be used to get row-wise average, standard deviation, median, maximum, minimum and number of numeric values. example:
-
sum(A:E) sum values row-wise in cols 1 to 5
-
sum(A:C, D:G, F) sum columns A to C, D to G, and F by row
-
sum(A2:D4)_mean calculate the mean of block from A2 to D4 by row
Note: This "row" mode syntax supported in Set Values and F(x)= is different and not compatible with scripting. See the sum() function for more information.
|
| Confidence(alpha, std, size[, dist])
|
Takes significance level alpha, population standard deviation std and sample size, returns the confidence interval for the population mean, using dist distribution. example:
-
confidence(0.05, 1.5, 100) returns 0.29399459768101.
|
| Geomean(vd)
|
Takes a vector vd, and returns the Geometric Mean.
-
Geomean(col(A)) returns the Geometric Mean of column A.
|
| Geosd(vd)
|
Takes a vector vd, and returns the Geometric Standard Deviation.
-
Geosd(col(A)) returns the Geometric SD of column A.
|
| Harmean(vd)
|
Takes a vector vd, and returns the Harmonic Mean.
-
Harmean(col(A)) returns the Harmonic mean of column A.
|
| histogram(vd, inc, min, max)
|
Takes a vector vd, bin width = inc, vd min and vd max, and generates data bins. Data points that fall on the upper edge of a bin are placed into the next higher bin.
|
| Kurt(vd)
|
Takes a vector vd, returns the kurtosis. example:
-
dataset ds = {1, 2, 3, 2, 3, 4, 5, 6, 4, 8}; kurt(ds) returns 0.39502164502164.
|
| lcl(vd[, level])
|
Takes a vector vd, returns the lower confidence limit at level. example:
-
lcl(col(A)) returns the lower confidence limit of column A at 0.95 level.
|
| Mad(vd)
|
Takes a vector vd, returns the Mean Absolute Deviation. example:
-
mad(col(A)) returns the Mean Absolute Deviation of column A.
|
| Mode(vd)
|
Takes a vector vd and returns the most frequently occurring number in vd. example:
aa = mode(col(A)) returens the most frequently occurring number in column A.
|
| Modes(vd)
|
Takes a vector vd and returns a vector of the most frequently occurring number(s) in vd. example:
Col(B) = mode(col(A)) outputs the most frequently occurring number in column A to column B.
|
| Percentile(vx, vy)
|
Takes a vector vx, returns the percentile values at each percent value specified in vy. example:
-
DATA1_A = normal(1000); DATA1_B = {1, 5, 25, 50, 75, 95, 99}; DATA1_C = percentile(DATA1_A, DATA1_B); returns a dataset DATA1_C that contains the percentiles of a normal distribution at 1%, 5%...99%.
|
| QCD2(n)
|
Takes a sample size n, returns the Quality Control D2 Factor. example:
|
| QCD3(n)
|
Takes a sample size n, returns the Quality Control D3 Factor. Factor D3 is the 3-sigma lower control limit in the X bar R chart. example:
|
| QCD4(n)
|
Takes a sample size n, returns the Quality Control D4 Factor. Factor D4 is the 3-sigma upper control limit in the X bar R chart. example:
|
| Skew(vd)
|
Takes a vector vd, returns the skewness (distribution asymmetry). example:
-
skew(col(a)) returns the skewness of the dataset in column A.
|
| ucl(vd[, level])
|
Takes a vector vd, returns the upper confidence level at level (0.95 by default). example:
-
ucl(col(a)) returns the upper confidence level of column A at 0.95 level.
|
| Emovavg(vd,n[,method])
|
Takes a vector vd and an integer n = time period, returns a vector of exponential moving averages. Option method specifies where calculation begins: 0 (default) = from point n; 1 = from 1st point. example:
-
for(ii=1;ii<=30;ii++) col(1)[ii] = ii; col(3)=emovavg(col(1),10, 1); //method II fills column 3 with values, calculated using starting point = 1.
|
| Mmovavg(vd,n)
|
Takes a vector vd, an integer n = time period, and returns a vector of modified moving averages. example:
-
for(ii=1;ii<=30;ii++) col(1)[ii] = ii; col(2)=mmovavg(col(1),10); fills column 2 with a modified moving average value at each point, starting with row 10.
|
| Movavg(vd,back,forward[,missing,method])
|
Takes a vector vd and returns the moving average of adjacent ranges [i-back, i+forward], for a point i (i = the current row number). Option missing determines whether to omit the missing values, and method specifies which method to use (the fast method or the the robust method).
-
for(ii=1;ii<=10;ii++) col(1)[ii] = ii; col(2)=movavg(col(1),0, 2); fills col(2) with adjacent average values at each point (Note that col(2)[9] = (col(1)[9]+col(1)[10])/2 and col(1)[10] = col(2)[10]).
|
| Movcoef(v1,v2,back,forward[,missing])
|
Takes two vectors v1 and v2 and returns a vector of moving correlation coefficients of adjacent ranges [i-back, i+forward], for a point i (i = the current row number). Option missing determines whether to omit the missing values. example:
-
wcol(4) = MovCoef(wcol(2), wcol(3), 20, 0);
fills the 4th column with moving correlation coefficients of col(2) and col(3), within the window [i-20. i]
|
| Movrms(vd,back[,forward,missing,method])
|
Takes a vector vd and returns the root mean square(RMS) of adjacent ranges [i-back, i+forward], for a point i (i = the current row number). Option missing determines whether to omit the missing values, and method specifies which method to use (the fast method or the the robust method). example:
-
col(B)=movrms(col(A),0, 2); fills col(B) with RMS at each point for data within the window [i, i+2]).
|
| Movslope(vx,vy[,n])
|
Takes two vectors, vx (independent) and vy (dependent), returns a vector of moving slope at each point. Optional n specifies window width (should be > 1). If n is even, 1 will be added. When n is not specified, the function returns a vector of one value which is the linear fit slope of the input. example:
-
col(C)=movslope(col(A),col(B),5); fills col(C) with slope at each point (first and last two cells are missing values).
|
| Tmovavg(vd,n[,missing, method])
|
Takes a vector vd and an integer n = time period, returns a vector of triangular moving averages. Option missing determine whether to omit the missing values, and method specifies which method to use (the fast method or the the robust method). example:
-
for(ii=1;ii<=30;ii++) col(1)[ii] = ii; col(2)=tmovavg(col(1),9); fills col(2) with triangular moving average values at each point, starting at point = 9.
|
| Wmovavg(vd,vw[,method])
|
Takes a vector vd (data to smooth) and vector vw (indexed weight factor), returns a vector of weighted moving averages. Option method specifies which method to use (the fast method or the the robust method). example:
-
for(ii=1;ii<=30;ii++) col(1)[ii] = ii; //data vector
for(ii=1;ii<=10;ii++) col(2)[ii] = ii/10; //weight vector
col(3)=wmovavg(col(1),col(2));
fills col(3) with the weighted moving average at each point, starting at point = 10.
|
Distribution Functions
Cumulative Distribution Functions (CDF)
| Name
|
Brief Description
|
| betacdf(x,a,b[,tail])
|
Computes beta cumulative distribution function at x, with parameters a and b. a and b must all be positive, and x must lie on the interval [0,1]. tail determines the returned probability is the lower tailed or upper tailed.
|
| binocdf(k,n,p)
|
Computes the lower tail, upper tail and point probabilities in given value k, associated with a Binomial distribution using the corresponding parameters in n, p.
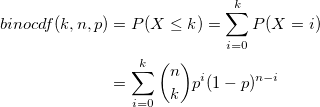
|
| bivarnormcdf(x,y,corre)
|
Computes the lower tail probability for the bivariate Normal distribution.
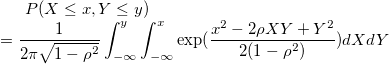
|
| chi2cdf(x,df[,tail])
|
Computes the lower/upper tail probability for the chi-square distribution with real degrees of freedom df.
|
| foldnormcdf(x,mu,sigma)
|
Computes the lower tail probability for the Folded Normal distribution.
|
| fcdf(f,ndf,fdf[,tail])
|
Computes the F cumulative distribution function at f, with degrees of freedom of the numerator variance ndf and denominator variance fdf. tail determines the returned probability is the lower tailed or upper tailed.
|
| gamcdf(g,a,b[,tail])
|
Computes the lower/upper tail probability for gamma variate g with real degrees of freedom, using shape parameter a and scale parameter b. tail determines the returned probability is the lower tailed or upper tailed.
|
| hygecdf(k,m,n,l)
|
Computes the lower tail probabilities in a given value, associated with a hypergeometric distribution using the corresponding parameters.
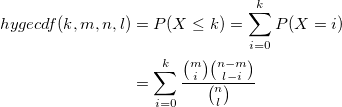
where n is the population size, m the number of success states in the population, and l the number of samples drawn.
|
| landaucdf(x,mu,sigma[,tail])
(2024b)
|
Computes the cumulative density function for the Landau distribution at x and with location parameter mu and scale parameter sigma. tail determines the returned probability is the lower tailed or upper tailed.
|
| logncdf(x,mu,sigma[,tail])
(2015 SR0)
|
Computes the probabilities of the specified tail type tail in a given value x, associated with a Lognormal distribution using the corresponding parameters mu and sigma. Lower tail probability will return if tail is not specified.
|
| ncbetacdf(x,a,b,lambda)
|
Computes the cdf with the lower tail of the non-central beta distribution.
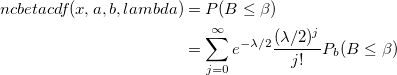
where
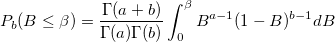 - which is the central beta probability function or incomplete beta function.
|
| ncchi2cdf(x,f,lambda)
|
Computes the probability associated with the lower tail of the non-central chi-square distribution.
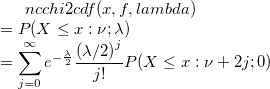
where 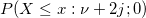 is a central is a central 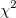 with with 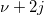 degrees of freedom. degrees of freedom.
|
| ncfcdf(f,df1,df2,lambda)
|
Computes the probability associated with the lower tail of the non-central digamma or variance-ratio distribution.
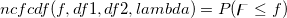 = =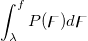 , ,
Where
![\begin{aligned}P(\digamma )&=\sum_{j=0}^\infty e^{-\lambda /2}\frac{(\lambda /2)^j}{j!}\cdot\frac{(\nu _1+2j)^{(\nu _1+2j)/2}\nu _2^{\nu _2/2}}{B((\nu _1+2j)/2,\nu _2/2)}\\&\cdot u^{(\nu _1+2j-2)/2}\left[ \nu _2+(\nu _1+2j)u\right] ^{-(\nu _1+2j+\nu _2)/2}\end{aligned} \begin{aligned}P(\digamma )&=\sum_{j=0}^\infty e^{-\lambda /2}\frac{(\lambda /2)^j}{j!}\cdot\frac{(\nu _1+2j)^{(\nu _1+2j)/2}\nu _2^{\nu _2/2}}{B((\nu _1+2j)/2,\nu _2/2)}\\&\cdot u^{(\nu _1+2j-2)/2}\left[ \nu _2+(\nu _1+2j)u\right] ^{-(\nu _1+2j+\nu _2)/2}\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-eb25f9ef60abdee3860cc90749b36385.png?v=0)
and 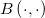 is the beta function. is the beta function.
|
| nctcdf(t,df,delta[,maxiter])
|
Computes the lower tail probability for the non-central Student's t-distribution.
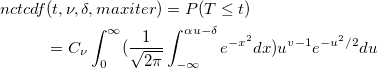
with
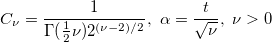
|
| normcdf(x[,tail])
|
Cmputes the probabilities of the specified tail type tail in a given value x, associated with a normal cumulative distribution.
|
| poisscdf(k,lambda)
|
Computes the lower tail probabilities in given value k, associated with a Poisson distribution using the corresponding parameters in lambda.
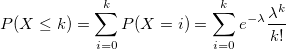
|
| srangecdf(q,v,group)
|
Computes the probability associated with the lower tail of the distribution of the Studentized range statistic.
![\begin{aligned}P(q)&=C\int_0^{+\infty }x^{\nu -1}e^{-\nu x^2/2}\{r\int_{-\infty }^{+\infty }\Phi (y)\\&\cdot\left[\Phi (y)-\Phi (y-qx)\right]^{r-1}dy\}dx\end{aligned} \begin{aligned}P(q)&=C\int_0^{+\infty }x^{\nu -1}e^{-\nu x^2/2}\{r\int_{-\infty }^{+\infty }\Phi (y)\\&\cdot\left[\Phi (y)-\Phi (y-qx)\right]^{r-1}dy\}dx\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-dc1ee2849c312d0bd7590d480983ae0f.png?v=0)
where
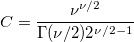 , , 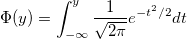
|
| tcdf(t,df[,tail])
|
Computes the probabilities of the specified tail type tail, associated with a cumulative distribution function of Student's t-distribution with the degree of freedom df.
|
| wblcdf(x,a,b)
|
Computes the lower tail Weibull cumulative distribution function for value x using the parameters a and b.
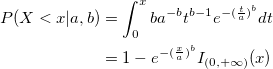
where 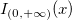 is the interval on which the Weibull CDF is not zero. is the interval on which the Weibull CDF is not zero.
|
Probability Density Functions (PDF)
| Name
|
Brief Description
|
| betapdf(x,a,b)
|
Returns the probability density function of the beta distribution with parameters a and b.
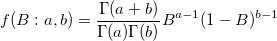
with 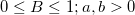
|
| binopdf(x,nt,p)
(2015 SR0)
|
Returns the probability density function of the binomial distribution with parameters nt and p.
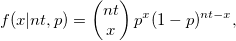
where 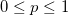 and and 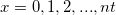 . .
|
| cauchypdf(x,a,b)
(8.6 SR0)
|
Cauchy probability density function (aka Lorentz distribution).
![f(x| a, b) = \frac{1}{\pi b \left[1 + \left(\frac{x - a}{b}\right)^2\right]}
= { 1 \over \pi } \left[ { b \over (x - a)^2 + b^2 } \right] f(x| a, b) = \frac{1}{\pi b \left[1 + \left(\frac{x - a}{b}\right)^2\right]}
= { 1 \over \pi } \left[ { b \over (x - a)^2 + b^2 } \right]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-8e85c2fcc57510fad5abdf7c7e52f68b.png?v=0)
|
| exppdf(x,lambda)
(8.6 SR0)
|
Returns the probability density function of the exponential distribution with rate parameter lambda, evaluated at the value x.
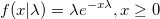
|
| foldnormpdf(x,mu,sigma)
|
Computes the probability density function at each of the values in X using the folder normal distribution with mean mu and standard deviation sigma.
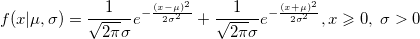
|
| gampdf(x,a,b)
(8.6 SR0)
|
Returns the Gamma probability density with parameters a and b.
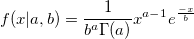
To obtain the scale and shape parameters a and b from a Gamma distributed dataset, you can use estimation function gamfit.
|
| ks2d(vx, vy[,bandwidth, grid, interp, binned])
(2020)
|
Returns the 2D kernel density at point (x, y) with specified bandwidth method and density method, where vx is a vector of X coordinate values and vy is a vector of Y coordinate values. Options for bandwidth method, grid (bandwidth method only), interpolation and density (applicable only when interp=1 (true)).
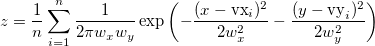
where n is the number of elements in vector vx or vy, index i indicates the ith element in vx or vy and optimal scales (wx, wy) are determined by estimation function kernel2width.
|
| ks2density(x,y,vx,vy,wx,wy)
(2015 SR0)
|
Returns the 2D kernel density at point (x, y) with respect to a function established by dataset (vx, vy) with scale (wx, wy).
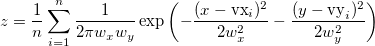
where n is the number of elements in vector vx or vy, index i indicates the ith element in vx or vy and optimal scales (wx, wy) are determined by estimation function kernel2width.
|
| ksdensity(x,vx,w)
(2015 SR0)
|
Returns the kernel density at x for a given vector vx with a bandwidth w.
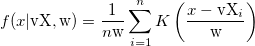
where n is the size of vector vX, K is the kernel function, Origin uses normal (Gaussian) kernel function, 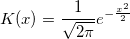 , and , and 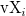 is the ith element in vector vX. is the ith element in vector vX.
|
| landaupdf(x,mu,sigma)
(2024b)
|
Compute the probability density function at each of the values in x using the Landau distribution with location paramter mu and scale parameter sigma.
|
| lappdf(x,mu,b)
(8.6 SR0)
|
Laplace probability density function.
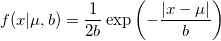
![= \frac{1}{2b}
\left\{\begin{matrix}
\exp \left( -\frac{\mu-x}{b} \right) & \mbox{if }x < \mu
\\[8pt]
\exp \left( -\frac{x-\mu}{b} \right) & \mbox{if }x \geq \mu
\end{matrix}\right.
= \frac{1}{2b}
\left\{\begin{matrix}
\exp \left( -\frac{\mu-x}{b} \right) & \mbox{if }x < \mu
\\[8pt]
\exp \left( -\frac{x-\mu}{b} \right) & \mbox{if }x \geq \mu
\end{matrix}\right.](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-a5a9b7eb31d29b76b9351919882b5ec3.png?v=0)
|
| lognpdf(x,mu,sigma)
(8.6 SR0)
|
Returns values at X of the lognormal probability density function with distribution parameters mu and sigma.
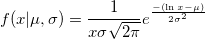
|
| normpdf(x,mu,sigma)
(8.6 SR0)
|
Computes the probability density function at each of the values in X using the normal distribution with mean mu and standard deviation sigma.
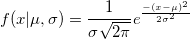
|
| poisspdf(x,lambda)
(8.6 SR0)
|
Computes the Poisson probability density function at each of the values in X using mean parameters in lambda.
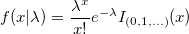
|
| wblpdf(x,a,b)
(8.6 SR0)
|
Returns the probability density function of the Weibull distribution with parameters a and b.
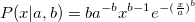
To obtain the scale and shape parameters a and b from a Weibull distributed dataset, you can use estimation function wblfit.
|
Inverse Cumulative Distribution Functions (INV)
| Name
|
Brief Description
|
| betainv(p,a,b)
|
Returns the inverse of the cumulative distribution function for a specified beta distribution.
|
| chi2inv(p,df)
|
Computes the inverse of the chi-square cumulative density function for the corresponding probabilities in X with parameters specified by nu.
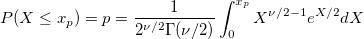
|
| finv(p,df1,df2)
|
Computes the inverse of F cumulative density function at p, with parameters df1 and df2.
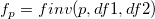
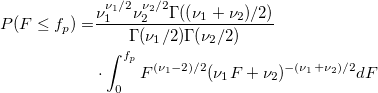
where 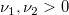 ; ; 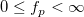
|
| foldnorminv(p,mu,sigma)
|
Computes the deviate, x, associated with the given lower tail probability, p, of the folded normal distribution, with distribution parameters mu and sigma.
|
| gaminv(p,a,b)
|
Computes the inverse of Gamma cumulative density function at p , with parameters a and b.
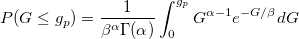
where 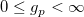 ; ;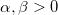
|
| Landauinv(p,mu,sigma)
(2024b)
|
Computes the inverse of the Landau cumulative density function at p , with location parameter mu and scale parameter sigma.
|
| logninv(p,mu,sigma)
(2015 SR0)
|
Computes the deviate,x, associated with the given lower tail probability,p, of the Lognormal distribution with parameters mu and sigma.
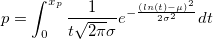
where 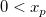
|
| norminv(p)
|
Computes the deviate, x, associated with the given lower tail probability, p, of the standardized normal distribution.
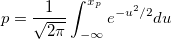
where 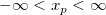
|
| srangeinv(p,v,ir)
|
Computes the deviate, x, associated with the lower tail probability of the distribution of the Studentized range statistic.
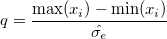
|
| tinv(p,df)
|
Computes the deviate associated with the lower tail probability of Student's t-distribution with real degrees of freedom.
![P(T\leq t_p)=\frac{\Gamma ((\nu +1)/2)}{\sqrt{\pi \nu }\Gamma (\nu /2)}\int_{-\infty }^{t_p}[1+\frac{T^2}\nu ]^{-(\nu +1)/2}dT P(T\leq t_p)=\frac{\Gamma ((\nu +1)/2)}{\sqrt{\pi \nu }\Gamma (\nu /2)}\int_{-\infty }^{t_p}[1+\frac{T^2}\nu ]^{-(\nu +1)/2}dT](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-08463b6d65b20a8e21302c2da6f15889.png?v=0) , , 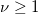
|
| wblinv(p,a,b)
|
Computes the inverse Weibull cumulative distribution function for the given probability using the parameters a and b.
![x_p=[aln(\frac 1{1-p}]^{(\frac 1b)}I_{[0,1]}(p) x_p=[aln(\frac 1{1-p}]^{(\frac 1b)}I_{[0,1]}(p)](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-ec6eae6ffd809a7050a0478ba2df12ef.png?v=0)
|
Data Generation Functions
Two functions in this category, rnd()/ran() and grnd(), return a value. All the other functions in this category return a range.
| Note: The seeding algorithm for Origin's methods of random number generation was changed for version 2016. For more information, see documentation for the system variable @ran.
|
| Name
|
Brief Description
|
| Data(x1,x2,inc)
|
Takes two values x1 and x2 and creates a dataset, ranging from x1 to x2, with an increment inc. If x1 = x2, function returns inc number of points with values = x1. Default for inc = 1. examples: col(A) = data(0,100,5) fills column A with numbers from 0 to 100, by increment = 5.
-
col(A) = data(10, 10, 5) fills the first five rows of column A with the number 10.
-
col(A) = data(1,100) fills column A with numbers from 1 to 100, by increment = 1.
|
| grnd()
|
Returns a value from a normally (Gaussian) distributed sample, with zero mean and unit standard deviation. The initial value and sequence of values are the same for each Origin session. No argument is needed. Commonly, the function is used to return a random value from a normal distribution of known mean and standard deviation, using the following expression: grnd()*sd+m. example:
-
aa=grnd()*0.30855+0.45701 might return 0.33882089669989.
|
| normal(npts[,seed])
|
Returns a range of npts. Values are random numbers with normal distribution (zero mean, unit standard deviation). If seed is omitted, a different seed is used each time the function is called. Can be used to fill a column with normally distributed random values, given a mean and standard deviation: normal(npts)*sd+m. example:
-
col(1) = normal(100)*2+5 fills column 1 with 100 random values with mean = 5 and sd = 2.
|
| pattern(vd, onerepeat, seqrepeat) and pattern(x1,x2,inc,onerepeat,seqrepeat)
|
Returns the generated patterned numeric or text data. pattern(vd, onerepeat, seqrepeat) will take input string series vd and repeat each element in vd onerepeat times and then repeat the whole string series seqrepeat times. pattern(x1,x2,inc,onerepeat,seqrepeat) will create a dataset range from x1 to x2 with increment inc, each element in the dataset will be repeated onerepeat times and then the whole dataset will be repeated seqrepeat times. Note that the elements in string series can be separated by pipe (|), comma(,), or space, or a range variable. example:
col(a)=pattern("Origin Lab", 2, 2); fills column A with "Origin Origin Lab Lab Origin Origin Lab Lab".col(b)=pattern(1,3,1,2,2); fill column B with "1 1 2 2 3 3 1 1 2 2 3 3".
|
| Poisson(n, mean [,seed])
|
Returns n random integers having a Poisson distribution with mean. Optional seed provides a seed for the number generator. example:
-
col(1)=Poisson(100,5,1) fills column 1 with 100 random values having a Poisson distribution with mean of 5.
|
| ran([seed]) and rnd([seed])
|
Returns a value between 0 and 1 from a uniformly distributed sample. They work exactly the same as rand function. If option seed is positive, sets the seed and returns 0. If seed is ≤ 0 or if no argument is provided, returns the next number in the random number sequence.
|
| rand([seed])
(2026)
|
Returns a value between 0 and 1 from a uniformly distributed sample. It works exactly the same as ran/rnd function. If option seed is positive, sets the seed and returns 0. If seed is ≤ 0 or if no argument is provided, returns the next number in the random number sequence.
|
| randbetween(n1, n2)
(2026)
|
Returns a random value between the given numbers n1 and n2. example:
-
col(b)[1]=randbetween(1,10) fills the first cell of collumn B with a random number between 1 and 10.
|
| uniform(npts [,seed]) and uniform(npts, vd)
|
Returns a range of npts. Option seed can be a value, data range, delimited string ("|", "," or space) or string array. If seed is a value, returns uniformly distributed random numbers. If seed is a data range or string array, returned values are randomly chosen from the data range or string(s). If seed is omitted, a different seed is used each time the function is called. This function also accepts a vector vd as an argument.
|
Lookup & Reference Functions
| Name
|
Brief Description
|
| Category(vd)$
(2020b)
|
Takes a vector vd of categorical data and returns all categories to a worksheet column. Category order follows source column. examples:
-
category([automobile]automobile!Make); // Set Values dialog form, "$" optional
-
range rA = [automobile]automobile!col(b); col(b) = category(rA)$; // LT script form, "$" needed
|
| Catindex(vd)
(2020b)
|
Takes a vector vd of categorical data and returns the category index for each of its elements to a worksheet column. examples:
|
| Catrows(vd[,option])
(2024b)
|
Takes a vector vd of categorical data and returns a pipe-separated list of all row indices by category. Optional option determine returning all/first/last index for each category. Category order follows source column. examples:
-
catrows([automobile]automobile!B); // Set Values dialog form, "$" optional
-
range rA = [automobile]automobile!col(b); col(b) = catrows(rA)$; // LT script form, "$" needed
|
| Cattext(n,vd)$
(2020b)
|
Takes a vector vd of categorical data and returns the nth category value. examples:
-
cattext(H,B); // Set Values dialog form, "$" optional
-
range rA = [automobile]automobile!col(b); col(b) = cattext(col(a),rA)$; // LT script form, "$" needed
|
| Findmasks(vd)
|
Takes a vector vd containing masked data, returns a vector of the indexes of masked points. example:
-
dataset aa=findmasks(col(b)); col(d)=aa fills column D with the row indices of masked data in column B.
|
| Firstpoint(vd)
|
Takes a vector vd, returns the first value of dataset vd. example:
-
aa = firstpoint(col(A)); get the first value of column A and assign it to variable aa.
|
| Idx(vBool)
|
Evaluates conditional expression vBool involving a single vector and returns a vector of integers containing the row indices of all records that meet the condition. examples:
-
idx(A); returns indices of true (1) values.
-
idx(B>=20 && B<=50); returns indices of values in B are between 20 and 50.
-
idx(left(A,5)$ == "Chris"); returns indices of values in A where first 5 letters are "Chris".
|
| Index(d,vd[,n])
|
Takes a vector vd of strictly monotonic data, returns the index of data point d. If option n = 0 (default) finds the value that is equal or closest to the value of d; n = 1 looks for ≤ d; n = 2 looks for ≥ d. If vd is not strictly monotonic or contains text, returns -2. example:
-
index(170,col(1)); returns the index of the value in column 1 that is equal or closest to 170.
|
| Lastpoint(vd)
|
Takes a vector vd(dataset), return the last value of dataset vd. example:
-
aa = lastpoint(col(A)); get the last value of column A and assign it to variable aa.
|
| List(val,vd)
|
Takes a vector vd, returns the dataset index number for first occurrence of val. If val is not found, the function returns 0. example:
-
list(3, col(A)) searches column A and returns the (row) index number where the value 3 first occurs.
|
| lookup(val,vs[,vref,option,Case])[$]
(2015 SR0)
|
Searches for val (string or number) in vector vs and returns the corresponding value from vector vref, or index of vs if vref is omitted. The returned value can be numeric or string. Match precision is set by option; Case = 0 (default) ignores case. example:
-
str1$ = Lookup("FSA", col(A), col(B))$; searches for string FSA in column A and assigns the corresponding value from column B to str1$.
-
nn = lookup(0.5,B) returns the index of the value in column B closest to 0.5.
|
| table(vd,vref,d[,option])[$]
(2015 SR0)
|
Searches for value d in vector vd, returns value in vref with the same index number. The return value can be numeric or string, depending on vref. Parameter option modifies search for parameter d: -1 (default) = function performs linear interpolation on vd vs vref and returns the interpolated value; 0 = finds nearest value that is ≤ d; 1 = finds nearest value that is ≥ d; 2 = finds nearest or equal value.
|
| unique(vs[, sort, occurrence, sort2])
(2018b)
|
Takes a vector vs and returns the unique values. Parameter sort decides whether to sort the returned unique values: 1 (default) = sort ascendingly; 0 = without sorting; 2 = sort descendingly. Parameter occurrence specifies how to reduce the duplicated values: 0 (default) = keep the first duplicated value; 1 = keep the last duplicated value. sort2 determines how to deal with the occurrence: 0 (default) = no occurrence sort, 1 = sort occurrence ascending. 2 = sort occurrence descending. example:
-
StringArray sA; sA = unique(col(a)); // assign unique values in col(a) to stringArray sA, in ascending order
|
| ReportCell(sBook$,sSheet$,sTable$,sRowRef$,sColRef$)
(2021b)
|
Access to report sheet table cell by specified book name sBook, sheet name sSheet, table name sTable and cell row&column reference sRowRef and sColRef. example: perform Gauss Fit on Book1 data, following formula
-
ReportCell("Book1", "FitNL1", "Summary", "R1", "a_Value") returns the fitted value of parameter "A"
Note: This function can not be used in cell formula.
|
| Xindex(x,vd[,option])
|
Takes a vector vd (Y dataset), returns the row index number of the value in the X dataset associated with vd, that is closest to value x. option determines which index is returned: 0 (default) = equal or closest from the left; 1 = equal or closest from the right; 2 = equal or closest, left or right. Requirements: (1) vd must be a designated Y column; (2) name of vd must correspond to an actual Y dataset; (3) the X dataset must be sorted in ascending order. example:
-
xindex(5,book1_g,1) returns the row index number for the x value that is equal or to the right of, (≥) 5.
|
| Xvalue(n,vd)
|
Takes a vector vd (Y or Z dataset), returns the corresponding X value at row number n. example:
-
xvalue(20,book4_c) returns the x value associated with column C at 20th row in column C of Book4.
|
| Errof(vd)
|
Takes a vector vd (dataset), returns the dataset (xEr/yEr) containing the error values of vd. example:
-
%a=errof(book1_b)might return book1_c.
|
| hasx(vd)
|
Takes a dataset vd and if vd is plotted against an x dataset in the active (graph) layer, returns 1; if not, returns 0. example:
-
aa=hasx(book1_b) returns 1 if the active graph layer contains a plot of column B.
|
| IsMasked(n,vd)
|
Takes a vector vd and if n = 0, returns the number of masked points. If n = data point index number, returns 1 if masked, 0 if not masked. example:
-
ismasked(0,book1_b) returns 77 if there are 77 masked points in dataset book1_b.
-
ismasked(8,book1_b) returns 0 if point n8 is not masked, or 1 if it is masked.
|
| Xof(vd)
|
Takes a vector name vd which is a Y dataset with an associated X dataset and returns a string containing the name of the X dataset. example:
-
%a = xof(book1_b); book1_c = %a; // e.g. after substitution : book1_c = book1_a puts the name of the X dataset associated with the Y dataset in column B and fills column C with the X values.
|
Data Manipulation Functions
| Name
|
Brief Description
|
| asc(str$)
|
Takes an input string and returns the ASCII code (decimal) for the first character in the string. This function does the same thing as the code function. example:
-
aa = asc($100); aa = returns 36.
|
| corr(vx,vy,k[, n])
|
Takes two datasets vx and vy, a lag size k and returns the correlation between the two datasets. Option n is the number of points. Lag parameter k can be scalar or vector. When k is a vector, function returns a vector; when a scalar, returns a scalar. example:
-
corr(col(1),col(2),data(1,10),50) returns the cross-correlation of the first 50 points of col(1) with col(2), using a lag size from 1 to 10.
|
| dropNA(vd[, text, end])
|
Takes a vector vd and remove missing and masked values. Optional parameter text determines how to deal with text, and end controls whether missing values are removed only at the beginning and end of the dataset, or removed entirely. example:
col(b)=dropNA(col(a))
|
| join(rA, rB, ...)
|
Takes two or more ranges, denoted as rA1:rA2, rB1:rB2,... and joins them into a single dataset. example:
-
total(join(col(a)[1]:col(a)[32],col(b)[1]:col(b)[32])); joins defined ranges and calculates total
-
=total(join(A1:A32,B1:B32)) // same as above, but syntax for cell or column formula only
|
| peaks(vd, width, minht)
|
Takes a vector vd, returns dataset of indices of peaks found using width and minht. width is number of points to each side of the test point. minht is in Y axis units. A peak at index i is minht greater than the data value at (i-width) or (i+width). example:
-
peaks(col(B), 3, 0.1) returns dataset of peak indices.
|
| rank(vd[, n])
|
Takes a dataset vd, sorts it and returns the ranked index. If n = 0 (default), vd is sorted in ascending order; if n = 1, in descending order. If duplicated values exist in vd, returns the average number of the ranked indexes for each duplicated value. example:
-
col(C)=rank(col(B),1); takes data in col(B) and output its ranked indexes to col(C)
|
| reverse(vd)
|
Takes a vector vd and reverses the order. example:
col(B)=reverse(col(A))
|
| sort(vd)
|
Takes a dataset, sorts it in ascending order and returns it. example:
-
%a=sort(book4_c); book4_d=%a takes the data in col(C), sorts it and fills col(D) with the result.
|
| treplace(vd,val1,val2[, cnd])
|
Replaces a dataset value with another when conditions cnd are met. Takes a dataset vd, compares each value to val1 with respect to option cnd and either replaces with val2 (or -val2) when comparison is true; or when false retains value or replaces with missing value ("--").
|
NAG Special Functions
Airy
| Name
|
Brief Description
|
| airy_ai(x)
|
Evaluates an approximation to the Airy function, Ai(x).
|
| airy_ai_deriv(x)
|
Evaluates an approximation to the derivative of the Airy function Ai(x).
|
| airy_bi(x)
|
Evaluates an approximation to the Airy function Bi(x).
|
| airy_bi_deriv(x)
|
Evaluates an approximation to the derivative of the Airy function Bi(x).
|
Bessel
| Name
|
Brief Description
|
| bessel_i0(x)
|
Bessel i0. Evaluates an approximation to the modified Bessel function of the first kind, I0(x).
|
| bessel_i0_scaled(x)
|
Bessel i0 scaled. Evaluates an approximation to 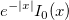
|
| bessel_i1(x)
|
Bessel i1. Evaluates an approximation to the modified Bessel function of the first kind,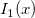 . .
|
| bessel_i1_scaled(x)
|
Bessel i1 scaled. Evaluates an approximation to 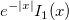
|
| bessel_i_nu(x,nu)
|
Bessel i nu. Evaluates an approximation to the modified Bessel function of the first kind I /4 (x) /4 (x)
|
| bessel_i_nu_scaled(x,nu)
|
Bessel i nu scaled. Evaluates an approximation to the modified Bessel function of the first kind 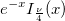
|
| bessel_j0(x)
|
Bessel j0. Evaluates the Bessel function of the first kind,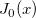
|
| bessel_j1(x)
|
Bessel j1. Evaluates an approximation to the Bessel function of the first kind 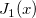
|
| bessel_k0(x)
|
Bessel k0. Evaluates an approximation to the modified Bessel function of the second kind,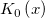
|
| bessel_k0_scaled(x)
|
Bessel k0 scaled. Evaluates an approximation to 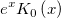
|
| Bessel_k1(x)
|
Bessel k1. Evaluates an approximation to the modified Bessel function of the second kind,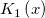
|
| bessel_k1_scaled(x)
|
Bessel k1 scaled. Evaluates an approximation to 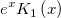
|
| bessel_k_nu(x,nu)
|
Bessel k nu. Evaluates an approximation to the modified Bessel function of the second kind 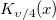
|
| bessel_k_nu_scaled(x,nu)
|
Bessel k nu scaled. Evaluates an approximation to the modified Bessel function of the second kind 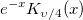
|
| bessel_y0(x)
|
Bessel y0. Evaluates the Bessel function of the second kind, 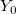 , x > 0. The approximation is based on Chebyshev expansions. , x > 0. The approximation is based on Chebyshev expansions.
|
| bessel_y1(x)
|
Bessel y1. Evaluates the Bessel function of the second kind, 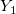 , x > 0. The approximation is based on Chebyshev expansions. , x > 0. The approximation is based on Chebyshev expansions.
|
| besseli(nu, z[, scale])
|
Evaluates the modified Bessel function of first kind.
|
| besselj(nu, z[, scale])
|
Evaluates the Bessel function of first kind.
|
| besselk(nu, z[, scale])
|
Evaluates the modified Bessel function of second kind,
|
| bessely(nu, z[, scale])
|
Evaluates the Bessel function of second kind.
|
Error
| Name
|
Brief Description
|
| erf(x)
|
The error function (or normal error integral).
|
| erfc(x)
|
Calculates an approximate value for the complement of the error function.
|
| erfcinv(dy)
|
Computes the value of the inverse complementary error function for specified y.
|
| erfcx(x)
|
The scaled complementary error function.
|
| erfi(c)
|
Take a complex or real number, and return the imaginary error function.
|
| erfinv(dy)
|
The inverse error function.
|
Gamma
Integral
| Name
|
Brief Description
|
| cos_integral(x)
|
NAG cosine integral function. Evaluates 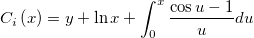
|
| cumul_normal(x)
|
Evaluates the cumulative Normal distribution function.
|
| cumul_normal_complem(x)
|
Evaluates an approximate value for the complement of the cumulative normal distribution function.
|
| elliptic_integral_rc(x,y)
|
NAG elliptical integral of the first kind. Calculates an approximate value for the integral 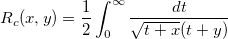
|
| elliptic_integral_rd(x,y,z)
|
NAG symmetrised elliptic integral of the second kind. Calculates an approximate value for the integral 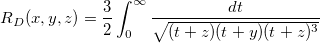
|
| elliptic_integral_rf(x,y,z)
|
NAG symmetrised elliptic integral of the first kind. Calculates an approximation to the integral 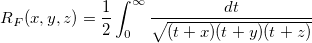
|
| elliptic_integral_rj(x,y,z,r)
|
NAG symmetrised elliptic integral of the third kind. Calculates an approximation to the integral 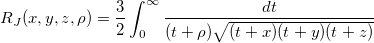
|
| exp_integral(x)
|
NAG exponential integral function. Evaluates 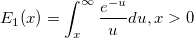
|
| fresnel_c(x)
|
NAG Fresnel integral function C. Evaluates an approximation to the Fresnel Integral 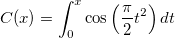 . .
|
| fresnel_s(x)
|
NAG Fresnel integral function S. Evaluates an approximation to the Fresnel Integral 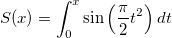 . .
|
| sin_integral(x)
|
NAG sine integral function. Evaluates 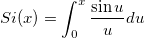
|
Kelvin
| Name
|
Brief Description
|
| kelvin_bei(x)
|
Evaluates an approximation to the Kelvin function bei x.
|
| kelvin_ber(x)
|
Evaluates an approximation to the Kelvin function ber x.
|
| kelvin_kei(x)
|
Evaluates an approximation to the Kelvin function kei x.
|
| kelvin_ker(x)
|
Evaluates an approximation to the Kelvin function ker x.
|
Miscellaneous
| Name
|
Brief Description
|
| jacobian_theta(k,x,q)
|
NAG Jacobian theta function. Computes the value of one of the Jacobian theta functions 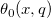 , , 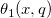 , , 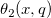 , , 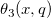 or or 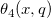 for a real argument x and non-negative q ≤ 1.. for a real argument x and non-negative q ≤ 1..
|
| lambertW(x[,branch,offset])
|
Calculates an approximate value for the real branches of Lambert's W function.
|
Fitting Functions
Multi-parameter functions in this category are used as built-in functions for Origin's nonlinear fitter. You can view the equation, a sample curve, and the function details for each multi-parameter function by opening the NLFit (Analysis: Fitting: Nonlinear Curve Fit). Then select the function of interest from the Function selection page.
For additional documentation on all the multi-parameter functions available from Origin's nonlinear curve fit, see this PDF on the OriginLab website. This document includes the mathematical description, a sample curve, a discussion of the parameters, and the LabTalk function syntax for each multi-parameter function.
Origin Basic Functions
| Name
|
Brief Description
|
| Allometric1(x,a,b)
|
Classical Freundlich Model, has been used in the study of allometry.
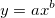
|
| Beta(x,y0,xc,A,w1,w2,w3)
|
Beta peak function for use in chromatography and spectroscopy.
![\begin{aligned}y=&y_0+A\left[1+\left(\frac{w_2+w_3-2}{w_2-1}\right)\left(\frac{x-x_c}{w_1}\right)\right]^{w_2-1}\\
&\cdot\left[1-\left(\frac{w_2+w_3-2}{w_3-1}\right)\left(\frac{x-x_c}{w_1}\right)\right]^{w_3-1}\end{aligned} \begin{aligned}y=&y_0+A\left[1+\left(\frac{w_2+w_3-2}{w_2-1}\right)\left(\frac{x-x_c}{w_1}\right)\right]^{w_2-1}\\
&\cdot\left[1-\left(\frac{w_2+w_3-2}{w_3-1}\right)\left(\frac{x-x_c}{w_1}\right)\right]^{w_3-1}\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-435026e27a6fde1c3d28aab6db0db1b4.png?v=0)
|
| Boltzmann(x, A1, A2, x0, dx)
|
Boltzmann Function - produce a sigmoidal curve.
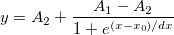
|
| dhyperbl(x,P1,P2,P3,P4,P5)
|
Double Rectangular Hyperbola Function.
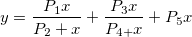
|
| ExpAssoc(x,y0,A1,t1,A2,t2)
|
Two-phase exponential association equation.
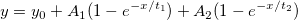
|
| ExpDec1(x,y0,A1,t1)
|
One-phase exponential decay function with time constant parameter.
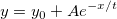
|
| ExpDec2(x,y0,A1,t1,A2,t2)
|
Two-phase exponential decay function with time constant parameters.
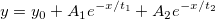
|
| ExpDec3(x,y0,A1,t1,A2,t2,A3,t3)
|
Three-phase exponential decay function with time constant parameters.
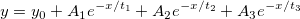
|
| ExpGrow1(x,y0,x0,A1,t1)
|
One-phase exponential growth with time offset, x0 should be fixed.
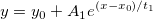
|
| ExpGrow2(x, y0, x0, A1, t1, A2, t2)
|
Two-phase exponential growth with time offset, x0 should be fixed.
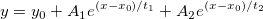
|
| Gauss(x, y0, xc, w, A)
|
Area version of Gaussian Function.
(y0 = offset, xc = center, w = width, A = area)
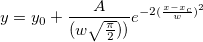
|
| GaussAmp(x,y0,xc,w,A)
|
Amplitude version of Gaussian peak function.
(y0 = offset, xc = center, w = width, A = amplitude)
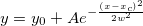
|
| Hyperbl(x, P1, P2)
|
Hyperbola funciton, also the Michaelis-Menten model in Enzyme Kinetics.
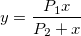
|
| Logistic(x, A1, A2, x0, p)
|
Logistic dose response in Pharmacology/Chemistry. Also known as 4PL or 4PLC.
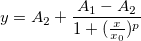
|
| LogNormal(x,y0,xc,w,A)
|
Probability density function of random variable whose logarithm is normally distributed.
![y=y_0+\frac A{\sqrt{2\pi }wx}e^{\frac{-\left[ \ln \frac x{x_c}\right] ^2}{2w^2}} y=y_0+\frac A{\sqrt{2\pi }wx}e^{\frac{-\left[ \ln \frac x{x_c}\right] ^2}{2w^2}}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-3220dc36e6a1075cbff267293aa3febe.png?v=0)
|
| Lorentz(x, y0, xc, w, A)
|
Lorentzian peak function with bell shape and much wider tails than Gaussian function.
(y0 = offset, xc = center, w = FWHM, A = area)
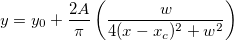
|
| Poisson(x,y0,r)
|
Poisson probability density function, a discrete probability distribution.
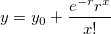
|
| Pulse(x, y0, x0, A, t1, P, t2)
|
Exponential pulse function(x >= x0 ? y : 0).
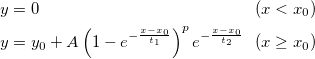
|
| Rational0(x,a,b,c)
|
Rational function with 1st order of numerator and 1st order of denominator.
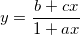
|
| Sine(x,y0,xc,w,A)
|
Sine wave function oscillates around a specified value.
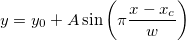
|
| Voigt(x,y0,xc,A,wG,wL)
|
Convolution of a Gaussian function and a Lorentzian function.
(y0 = offset, xc = center, A =area, wG = Gaussian FWHM, wL = Lorentzian FWHM)
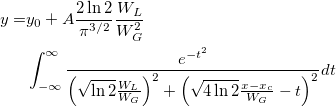
|
Implicit
| Name
|
Brief Description
|
| Circle(x,y,xc,yc,r)
|
Implicit circle equation with parameters circle center and radius.
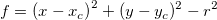
|
| Ellipse(x,y,xc,yc,a,b)
|
Implicit ellipse equation whose major and minor axes coincide with XY axes.
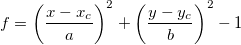
|
| ModDiode(V,I,T,Is,Rs,n,Rsh)
|
Implicit modified diode equation.
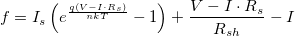
|
| PlaneMod(x,y,z,theta,phi,d)
|
Modified implicit plane function defined by its normal direction.
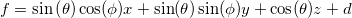
|
| SolarCellIV(V,I,T,Is,Rs,n,Rsh,IL)
|
Solar cell I-V curve.
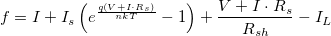
|
Exponential
| Name
|
Brief Description
|
| Asymptotic1(x,a,b,c)
|
Asymptotic Regression Model - 1st parameterization.
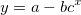
|
| BoxLucas1(x,a,b)
|
Box Lucas model, same as one-phase association equation with zero offset.
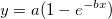
|
| BoxLucas1Mod(x,a,b)
|
a parameterization of Box Lucas Model.
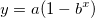
|
| BoxLucas2(x,a1,a2)
|
Box Lucas model for two phase.
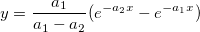
|
| Chapman(x,a,b,c)
|
Chapman-Richards function to describe the cumulative growth curve.
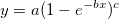
|
| Exp1p1(x,A)
|
One-Parameter Exponential Function.
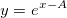
|
| Exp1p2(x,A)
|
One-Parameter Exponential Function.
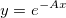
|
| Exp1p2Md(x,B)
|
One-Parameter Exponential Function.
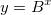
|
| Exp1P3(x,A)
|
One-Parameter Exponential Function.
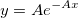
|
| Exp1P3Md(x,B)
|
One-Parameter Exponential Function.
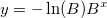
|
| Exp1P4(x,A),
|
One-parameter asymptotic exponential function.
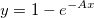
|
| Exp1P4Md(x,B)
|
Another form of one-parameter asymptotic exponential function.
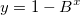
|
| Exp2P(x,a,b)
|
Two-Parameter Exponential Function.
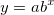
|
| Exp2PMod1(x,a,b),
|
Two-Parameter Exponential Function.
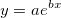
|
| Exp2PMod2(x,a,b),
|
Two-Parameter Exponential Function.
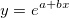
|
| Exp3P1(x,a,b,c),
|
Inverted offset exponential function.
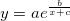
|
| Exp3P1Md(x,a,b,c),
|
Another form of inverted offset exponential function.
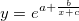
|
| Exp3P2(x,a,b,c),
|
Exponential function whose exponent is a 2nd order polynomial.
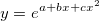
|
| ExpAssoc(x,y0,A1,t1,A2,t2)
|
Two-phase exponential association equation.
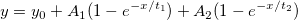
|
| ExpAssoc1(x,TD,Yb,A,Tau)
(2017 SR0)
|
One-phase exponential association equation.
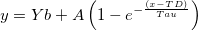
|
| ExpAssoc2(x,TD1,TD2,Yb,A1,A2,Tau1,Tau2)
(2017 SR0)
|
Biphasic exponential association equation.
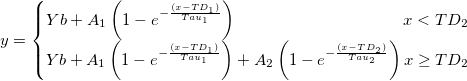
|
| ExpAssocDelay1(x,TD,Yb,A,Tau)
(2017 SR0)
|
One-phase exponential association equation with plateau before exponential begins.
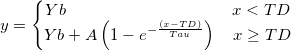
|
| ExpAssocDelay2(x,TD1,TD2,Yb,A1,A2,Tau1,Tau2)
(2017 SR0)
|
Biphasic exponential association equation with plateau before exponential begins.
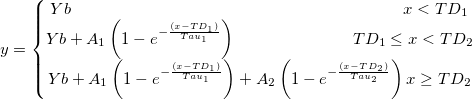
|
| Exponential(x,y0,A,R0)
|
Exponential growth function with rate constant parameter.
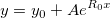
|
| ExpDec1(x,y0,A1,t1)
|
One-phase exponential decay function with time constant parameter.
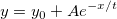
|
| ExpDec2(x,y0,A1,t1,A2,t2)
|
Two-phase exponential decay function with time constant parameters.
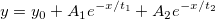
|
| ExpDec3(x,y0,A1,t1,A2,t2,A3,t3)
|
Three-phase exponential decay function with time constant parameters.
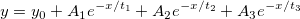
|
| ExpDecay1(x,y0,x0,A1,t1)
|
One-phase exponential decay function with time offset, x0 should be fixed.
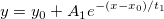
|
| ExpDecay2(x, y0, x0, A1, t1, A2, t2)
|
Two-phase exponential decay function with time offset, x0 should be fixed.
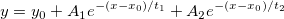
|
| ExpDecay3(x,y0,x0,A1,t1,A2,t2,A3,t3)
|
Three-phase exponential decay function with time offset, x0 should be fixed.
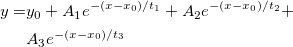
|
| ExpGro1(x,y0,A1,t1)
|
One-phase exponential growth function with time constant parameter.
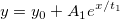
|
| ExpGro2(x,y0,A1,t1,A2,t2)
|
Two-phase exponential growth function with time constant parameters.
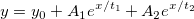
|
| ExpGro3(x,y0,A1,t1,A2,t2,A3,t3)
|
Three-phase exponential growth function with time constant parameters.
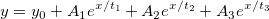
|
| ExpGrow1(x,y0,x0,A1,t1)
|
One-phase exponential growth with time offset, x0 should be fixed.
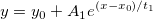
|
| ExpGrow2(x, y0, x0, A1, t1, A2, t2)
|
Two-phase exponential growth with time offset, x0 should be fixed.
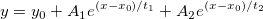
|
| ExpGrow3Dec2(x,y0,xc,Ag1,tg1,Ag2,tg2,Ag3,tg3,Ad1,td1,Ad2,td2)
(2015 SR0)
|
Exponential function with three growth and two decay phases.
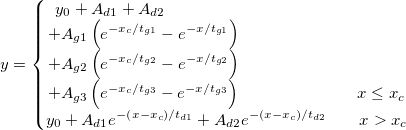
|
| ExpGrowDec(x,y0,xc,Ag,tg,Ad,td)
(2015 SR0)
|
Exponential function with one growth and one decay phases.
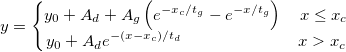
|
| ExpLinear(x,p1,p2,p3,p4)
|
Exponential Linear Combiantion.
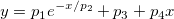
|
| Langevin(x,y0,xc,C)
|
Langevin function used in paramagnetism with three parameters.
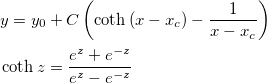
|
| LangevinMod(x,y0,xc,C,s)
(2015 SR0)
|
Scale modified Langevin function.
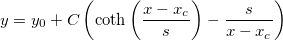
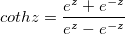
|
| PIPlatt(x,Pm,alpha)
(2017 SR0)
|
Model of photosynthesis vs. irradiance curve by Platt
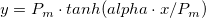
|
| PIPlatt2(x,Ps,alpha,beta)
(2017 SR0)
|
Model of photosynthesis vs. irradiance curve with photoinhibition by Platt
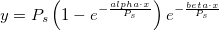
|
| PIWebb(x,Pm,alpha)
(2017 SR0)
|
Model of photosynthesis vs. irradiance curve by Webb
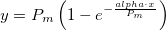
|
| MnMolecular(x,A,xc,k),
|
Monomolecular growth model.
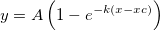
|
| MnMolecular1(x,A1,A2,k)
|
Another form of Monomolecular growth model.
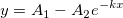
|
| Shah(x,a,b,c,r)
|
Exponential decay function combined with a linear function.
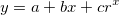
|
| Stirling(x,a,b,k)
|
Exponential growth function with slope at zero for parameter.
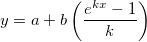
|
| YldFert(x,a,b,r)
|
Yield-fertilizer model in Agriculture and Learning curve in psychology.
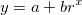
|
| YldFert1(x,a,b,k)
|
Yield-fertilizer model in Agriculture and Learning curve in psychology.
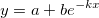
|
Growth/Sigmoidal
| Name
|
Brief Description
|
| BiDoseResp(x,A1,A2,LOGx01,LOGx02,h1,h2,p)
|
Biphasic Dose Response Function.
![\begin{aligned}y=&A_1+(A_2-A_1)\bigg[\frac{p}{1+10^{(LOGx01-x)h1}}+\\
&\frac{1-p}{1+10^{(LOGx02-x)h2}}\bigg]\end{aligned} \begin{aligned}y=&A_1+(A_2-A_1)\bigg[\frac{p}{1+10^{(LOGx01-x)h1}}+\\
&\frac{1-p}{1+10^{(LOGx02-x)h2}}\bigg]\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-5a931673f336d3539f282df4fd1d9752.png?v=0)
|
| BiHill(x,Pm,Ka,Ki,Ha,Hi)
(2015 SR0)
|
Biphasic Hill Equation.
![y=\frac{P_{m}}{[1+(\frac{K_{a}}{x})^{H_{a}}][1+(\frac{x}{K_{i}})^{H_{i}}]} y=\frac{P_{m}}{[1+(\frac{K_{a}}{x})^{H_{a}}][1+(\frac{x}{K_{i}})^{H_{i}}]}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-ce7a5e8d7f9f7b024ec8fa9326a65009.png?v=0)
|
| BoltzIV(x,vhalf,dx,gmax,vrev)
|
Transformed Boltzmann function for IV data.
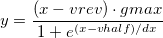
|
| Boltzmann(x, A1, A2, x0, dx)
|
Boltzmann Function - produce a sigmoidal curve.
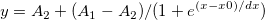
|
| DoseResp(x,A1,A2,LOGx0,p)
|
Dose-response curve with variable Hill slope given by parameter 'p'.
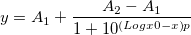
|
| DoubleBoltzmann(x,y0,A,frac,x01,x02,k1,k2)
|
Double Boltzmann Function, sum of two Boltzmann functions.
![y=y_0+A\left[\frac{p}{1+e^{\frac{x-x_{01}}{k_1}}}+\frac{1-p}{1+e^{\frac{x-x_{02}}{k_2}}}\right] y=y_0+A\left[\frac{p}{1+e^{\frac{x-x_{01}}{k_1}}}+\frac{1-p}{1+e^{\frac{x-x_{02}}{k_2}}}\right]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-649e5dcc558a3cbe663ecabcca96fc0e.png?v=0)
|
| Hill(x,Vmax,k,n)
|
Hill function to determine ligand concentration and maximum number of binding sites.
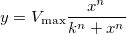
|
| Hill1(x,START,END,k,n)
|
Modified Hill function with offset.
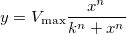
|
| Logistic(x, A1, A2, x0, p)
|
Logistic dose response in Pharmacology/Chemistry. Also known as 4PL or 4PLC.
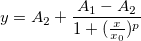
|
| Logistic5(x,Amin,Amax,x0,h,s)
|
Five parameters logistic function. Also known as 5PL or 5PLC.
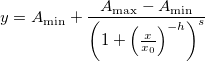
|
| MichaelisMenten(x,Vmax,Km)
|
Michaelis Menten function to describe relation of concentration of substrate and enzyme velocity.
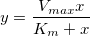
|
| SGompertz(x,a,xc,k)
|
Gompertz Growth Model for Popuplation Studies, Animal Growth.
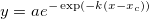
|
| Slogistic1(x,a,xc,k)
|
Sigmoidal Logistic function, type 1.
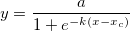
|
| SLogistic2(x,y0,a,Wmax)
|
Sigmoidal Logistic function, type 2.
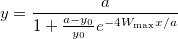
|
| SLogistic3(x,a,b,k)
|
Sigmoidal Logistic function, type 3.
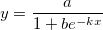
|
| SRichards1(x,a,xc,d,k)
|
Sigmoidal Richards function, type 1.
![y=\left[ a^{1-d}-e^{-k\left( x-x_c\right) }\right] ^{1/\left( 1-d\right) },d<1 y=\left[ a^{1-d}-e^{-k\left( x-x_c\right) }\right] ^{1/\left( 1-d\right) },d<1](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-2cef129b1d404b1a78cbef3fef041d59.png?v=0)
![y=\left[ a^{1-d}+e^{-k\left( x-x_c\right) }\right] ^{1/\left( 1-d\right) },d>1 y=\left[ a^{1-d}+e^{-k\left( x-x_c\right) }\right] ^{1/\left( 1-d\right) },d>1](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-e2d761428ae5521d47b9f95878bad13c.png?v=0)
|
| SRichards2(x,a,xc,d,k)
|
Sigmoidal Richards function, type 2.
![y=a\left[ 1+\left( d-1\right) e^{-k\left( x-x_c\right) }\right] ^{1/\left( 1-d\right) },d\neq 1 y=a\left[ 1+\left( d-1\right) e^{-k\left( x-x_c\right) }\right] ^{1/\left( 1-d\right) },d\neq 1](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-e5c7adcfd74d6710ffd6a0ca10d00c76.png?v=0)
|
| SWeibull1(x,A,xc,d,k)
|
Sigmoidal Weibull funciton, type 1.
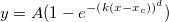
|
| SWeibull2(x,a,b,d,k)
|
Sigmoidal Weibull function, type 2.
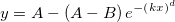
|
Hyperbola
| Name
|
Brief Description
|
| Dhyperbl(x,P1,P2,P3,P4,P5)
|
Double Rectangular Hyperbola Function.
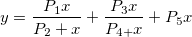
|
| Hyperbl(x, P1, P2)
|
Hyperbola funciton, also the Michaelis-Menten model in Enzyme Kinetics.
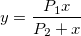
|
| HyperbolaGen(x,a,b,c,d)
|
Generalized Hyperbola function.
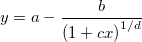
|
| HyperbolaMod(x,T1,T2)
|
Modified hyperbola function.
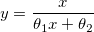
|
| RectHyperbola(x,a,b)
|
Rectangular Hyperbola Function.
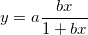
|
Logarithm
| Name
|
Brief Description
|
| Bradley(x,a,b)
|
Double logarithmic reciprocal function.
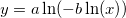
|
| Log2P1(x,a,b),
|
Two-parameter Logarithm function.
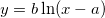
|
| Log2P2(x,a,b)
|
Logarithmic transform function.
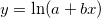
|
| Log3P1(x,a,b,c)
|
Linear logarithmic transform function.
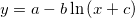
|
| Logarithm(x,A)
|
One-parameter logarithm.
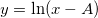
|
Peak Functions
| Name
|
Brief Description
|
| Asym2Sig(x,y0,xc,A,w1,w2,w3)
|
Asymmetric double Sigmoidal function.
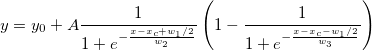
|
| Beta(x,y0,xc,A,w1,w2,w3)
|
Beta peak function for use in chromatography and spectroscopy.
![\begin{aligned}y=&y_0+A\left[1+\left(\frac{w_2+w_3-2}{w_2-1}\right)\left(\frac{x-x_c}{w_1}\right)\right]^{w_2-1}\\&\cdot\left[1-\left(\frac{w_2+w_3-2}{w_3-1}\right)\left(\frac{x-x_c}{w_1}\right)\right]^{w_3-1}\end{aligned} \begin{aligned}y=&y_0+A\left[1+\left(\frac{w_2+w_3-2}{w_2-1}\right)\left(\frac{x-x_c}{w_1}\right)\right]^{w_2-1}\\&\cdot\left[1-\left(\frac{w_2+w_3-2}{w_3-1}\right)\left(\frac{x-x_c}{w_1}\right)\right]^{w_3-1}\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-076b4d5daaea23eccbea1ff441b581bc.png?v=0)
|
| Bigaussian(x,y0,xc,H,w1,w2)
|
Bi-Gaussian peak function used to fit asymmetric peak.
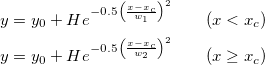
|
| CCE(x,y0,xc1,A,w,k2,xc2,B,k3,xc3)
|
Chesler-Cram Peak Function for use in chromatography.
![\begin{aligned}y=&y_0+A\bigg[e^{-\frac{\left(x-x_{c1}\right)^2}{2w}}+B(1-0.5(1-\tanh (k_2(x-\\
&x_{c2}))))e^{-0.5k_3(|x-x_{c3}|+(x-x_{c3}))}\bigg]\end{aligned} \begin{aligned}y=&y_0+A\bigg[e^{-\frac{\left(x-x_{c1}\right)^2}{2w}}+B(1-0.5(1-\tanh (k_2(x-\\
&x_{c2}))))e^{-0.5k_3(|x-x_{c3}|+(x-x_{c3}))}\bigg]\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-8ba1f583218740b063ba686def196277.png?v=0)
|
| ECS(x,y0,xc,A,w,a3,a4)
|
Edgeworth-Cramer Peak Function for use in chromatography.
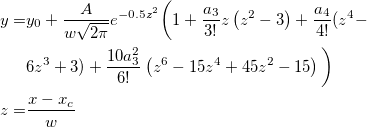
|
| Extreme(x,y0,xc,w,A)
|
Particular case of extreme function, Gumbel probability density function.
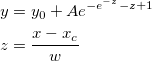
|
| Gauss(x, y0, xc, w, A)
|
Area version of Gaussian Function.
(y0 = offset, xc = center, w = width, A = area)
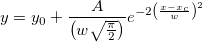
|
| GaussAmp(x,y0,xc,w,A)
|
Amplitude version of Gaussian peak function.
(y0 = offset, xc = center, w = width, A = amplitude)
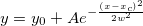
|
| Gaussian(x,y0,xc,A,w)
|
FWHM version of Gaussian Function.
(y0 = base, xc = center, A = area, w = FWHM)
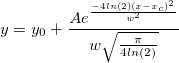
|
| GaussMod(x,y0,A,xc,w,t0)
|
Exponentially modified Gaussian (EMG) peak function for use in Chromatography.
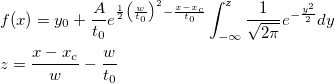
|
| GCAS(x,y0,xc,A,w,a3,a4)
|
Gram-Charlier peak function for use in chromatography.

|
| Giddings(x,y0,xc,w,A)
|
Giddings peak function for use in Chromatography.
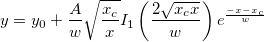
|
| InvsPoly(x,y0,xc,w,A,A1,A2,A3)
|
Inverse polynomial peak function with center.
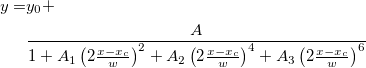
|
| Laplace(x,y0,a,b)
|
Laplace probability density function.
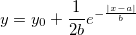
|
| Logistpk(x,y0,xc,w,A)
|
Logistic peak function, also called Hubbert function.
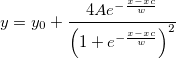
|
| LogNormal(x,y0,xc,w,A)
|
Probability density function of random variable whose logarithm is normally distributed.
![y=y_0+\frac A{\sqrt{2\pi }wx}e^{\frac{-\left[ \ln \frac x{xc}\right] ^2}{2w^2}} y=y_0+\frac A{\sqrt{2\pi }wx}e^{\frac{-\left[ \ln \frac x{xc}\right] ^2}{2w^2}}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-e98dcb616116ac2349df7544a55b124f.png?v=0)
|
| Lorentz(x, y0, xc, w, A)
|
Lorentzian peak function with bell shape and much wider tails than Gaussian function.
(y0 = offset, xc = center, w = FWHM, A = area)
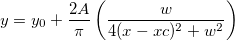
|
| PearsonIV(x,y0,A,m,v,alpha,lam)
|
Pearson Type IV distribution for negative discriminant, suited to model pull distributions.
![\begin{aligned}&y=y_0+Ak\left[1+\left(\frac{x-\lambda\!}{\alpha\!}\right)\right]^{-m}e^{-v\tan^{-1}\left(\frac{x-\lambda\!}{\alpha\!}\right) } \\
&k=\frac{2^{2m-2}|\Gamma\!\left(m+iv/2\right)|^2}{\pi\!\alpha\!\Gamma\!\left(2m-1\right)}, m>\frac{1}{2}\end{aligned} \begin{aligned}&y=y_0+Ak\left[1+\left(\frac{x-\lambda\!}{\alpha\!}\right)\right]^{-m}e^{-v\tan^{-1}\left(\frac{x-\lambda\!}{\alpha\!}\right) } \\
&k=\frac{2^{2m-2}|\Gamma\!\left(m+iv/2\right)|^2}{\pi\!\alpha\!\Gamma\!\left(2m-1\right)}, m>\frac{1}{2}\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-2578f3f3d1060040453114eb42fee3a2.png?v=0)
|
| PearsonVII(x,y0,xc,A,w,m)
|
Pearson Type VII peak function is a Lorentz function raised to a power.
![\begin{aligned}&y=y_0+A\frac{2\Gamma (\mu)\sqrt{2^{\frac{1}{\mu}}-1}}{\sqrt{\pi }\Gamma \left( \mu-\frac 12\right) w}\bigg[ 1+4\frac{2^{\frac{1}{\mu}}-1}{w^2}\left( x-x_c\right) ^2\bigg] ^{-\mu}\\
&m=\mu\end{aligned} \begin{aligned}&y=y_0+A\frac{2\Gamma (\mu)\sqrt{2^{\frac{1}{\mu}}-1}}{\sqrt{\pi }\Gamma \left( \mu-\frac 12\right) w}\bigg[ 1+4\frac{2^{\frac{1}{\mu}}-1}{w^2}\left( x-x_c\right) ^2\bigg] ^{-\mu}\\
&m=\mu\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-3dfdbeab0848b14621c0b803f539eb3b.png?v=0)
|
| PsdVoigt1(x,y0,xc,A,w,mu)
|
Pseudo-Voigt function, linear combination of Gaussian function and Lorentzian function.
(y0 = offset, xc = center, A = area, w = FWHM, mu = profile shape factor)
![\begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac w{4\left( x-x_c\right) ^2+w^2}\\
&+\left( 1-m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w}e^{-\frac{4\ln 2}{w^2}\left( x-x_c\right) ^2}\bigg]\end{aligned} \begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac w{4\left( x-x_c\right) ^2+w^2}\\
&+\left( 1-m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w}e^{-\frac{4\ln 2}{w^2}\left( x-x_c\right) ^2}\bigg]\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-a2bbe7b2678afc56a46e94e4092a69a5.png?v=0)
|
| PsdVoigt2(x,y0,xc,A,wG,wL,mu)
|
Pseudo-Voigt function, linear combination of Gaussian and Lorentzian with different FWHM.
(y0 = offset, xc = center, A =area, wG=Gaussian FWHM, wL=Lorentzian FWHM, mu = profile shape factor)
![\begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac{w_L}{4\left( x-x_c\right) ^2+w_L^2}+\\
&\left( 1-m_u\right) \frac{\sqrt{4\ln2}}{\sqrt{\pi}w_G}e^{-\frac{4\ln 2}{w_G^2}\left( x-x_c\right) ^2}\bigg] \end{aligned} \begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac{w_L}{4\left( x-x_c\right) ^2+w_L^2}+\\
&\left( 1-m_u\right) \frac{\sqrt{4\ln2}}{\sqrt{\pi}w_G}e^{-\frac{4\ln 2}{w_G^2}\left( x-x_c\right) ^2}\bigg] \end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-71ad34b7a8ff4400fafbd7187d8bc5ff.png?v=0)
|
| Voigt(x,y0,xc,A,wG,wL)
|
Convolution of a Gaussian function (wG for FWHM) and a Lorentzian function.
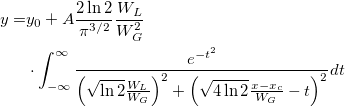
|
| Weibull3(x,y0,xc,A,w1,w2)
|
Amplitude version of Weibull peak function.
![\begin{aligned}S&=\frac{x-x_c}{w_1}+\left( \frac{w_2-1}{w_2}\right) ^{\frac 1{w_2}}\\
y&=y_0+A\left( \frac{w_2-1}{w_2}\right) ^{\frac{1-w_2}{w_2}}\left[ S\right] ^{w_2-1}e^{-\left[ S\right] ^{w_2}+\left( \frac{w_2-1}{w_2}\right) }\end{aligned} \begin{aligned}S&=\frac{x-x_c}{w_1}+\left( \frac{w_2-1}{w_2}\right) ^{\frac 1{w_2}}\\
y&=y_0+A\left( \frac{w_2-1}{w_2}\right) ^{\frac{1-w_2}{w_2}}\left[ S\right] ^{w_2-1}e^{-\left[ S\right] ^{w_2}+\left( \frac{w_2-1}{w_2}\right) }\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-508a00fe65b3a935b87f1c9096d0656a.png?v=0)
|
Piecewise
| Name
|
Brief Description
|
| PWL2(x,a1,k1,xi,k2)
|
Piecewise linear function with two segments.
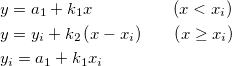
|
| PWL3(x,a1,k1,xi1,k2,xi2,k3)
|
Piecewise linear function with three segments.
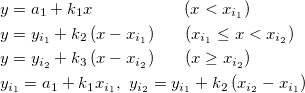
|
Polynomial
| Name
|
Brief Description
|
| Constant(x,y0)
|
Constant base line function.
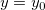
|
| Cubic(x,A,B,C,D)
|
Third order polynomial.
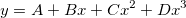
|
| Line(x,A,B)
|
Line function with slope and intercept.
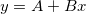
|
| LineMod(x,a,b)
|
Line function with x-intercept and slope for parameters.
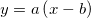
|
| Parabola(x,A,B,C)
|
Second order polynomial.
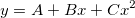
|
| Poly(x, a0, a1, a2, a3, a4, a5, a6, a7, a8, a9)
|
9th order polynomial.
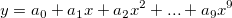
|
| Poly4(x,A0,A1,A2,A3,A4)
|
4th order Polynomial function.
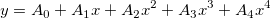
|
| Poly5(x,A0,A1,A2,A3,A4,A5)
|
5th order polynomial function.
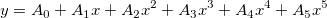
|
Power
| Name
|
Brief Description
|
| Allometric1(x,a,b)
|
Classical Freundlich Model, has been used in the study of allometry.
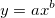
|
| Allometric2(x,a,b,c)
|
An extension of Classical Freundlich Model.
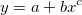
|
| Belehradek(x,a,b,c)
|
X shifted power function.
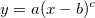
|
| BlNeld(x,a,b,c,f)
|
Bleasdale-Nelder function for yield-density model.
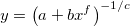
|
| BlNeldSmp(x,a,b,c)
|
Simplified Bleasdale-Nelder Model.
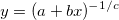
|
| FarazdaghiHarris(x,a,b,c)
|
Farazdaghi-Harris Model for use in yield-density study.
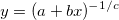
|
| FreundlichEXT(x,a,b,c)
|
Extended Freundlich adsorption isotherm equation.
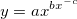
|
| Gunary(x,a,b,c)
|
Gunary adsorption isotherm equation.
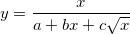
|
| LangmuirEXT1(x,a,b,c),
|
Extended Langmuir adsorption isotherm equation.
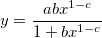
|
| LangmuirEXT2(x,a,b,c)
|
Another form of extended Langmuir adsorption isotherm equation.
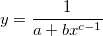
|
| Pareto(x,A)
|
Pareto cumulative distribution function with one parameter, a power law probability distribution.
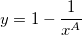
|
| Pow2P1(x,a,b),
|
Scaled Pareto function.
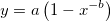
|
| Pow2P2(x,a,b),
|
two-parameter power function.
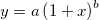
|
| Pow2P3(x,a,b)
|
Pareto transform function.
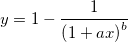
|
| Power(x,A)
|
One-parameter Power function.
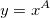
|
| Power0(x,y0,xc,A,P)
|
Symmetric Power function with offset.
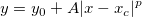
|
| Power1(x,xc,A,P)
|
Symmetric Power function.
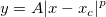
|
| Power2(x,xc,A,pl,pu)
|
Asymmetric Power function.
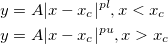
|
Rational
| Name
|
Brief Description
|
| BET(x,a,b)
|
Brunauer-Emmett-Teller (BET) adsorption equation.
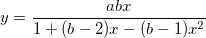
|
| BETMod(x,a,b)
|
Modified BET Model.
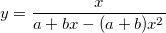
|
| Holliday(x,a,b,c)
|
Holliday Model - a Yield-density model for use in agriculture.
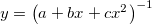
|
| Holliday1(x,a,b,c)
|
extended Holliday Model.
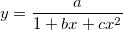
|
| Nelder(x,a,b0,b1,b2)
|
Nelder Model - a Yeild-fertilizer model in agriculture.
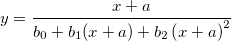
|
| Rational0(x,a,b,c)
|
Rational function with 1st order of numerator and 1st order of denominator.
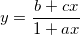
|
| Rational1(x,a,b,c)
|
Another form of Rational0 function with constant coefficient in numerator normalized.
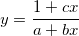
|
| Rational2(x,a,b,c)
|
Another form of Rational0 function with coefficient of x in denominator normalized.
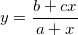
|
| Rational3(x,a,b,c)
|
Another form of Rational0 function with coefficient of x in numerator normalized.
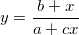
|
| Rational4(x,a,b,c)
|
Another form of Rational0 function with sum of constant and a rational function.
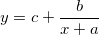
|
| Rational5(x,a,b,c,d)
|
Rational function with 1st order of numerator and 2nd order of denominator.
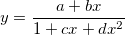
|
| Reciprocal(x,a,b)
|
two parameter linear reciprocal function.
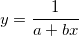
|
| Reciprocal0(x,A)
|
One-parameter (slope) linear reciprocal function.
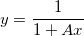
|
| Reciprocal1(x,A)
|
One-parameter (intercept) linear reciprocal function.
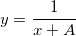
|
| ReciprocalMod(x,a,b)
|
Another form of Reciprocal function with constant coefficient in denominator normalized.
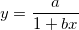
|
Waveform
| Name
|
Brief Description
|
| SawtoothWave(x,x0,y0,A,T)
|
Sawtooth wave, a periodic function consisting of extreme case asymmetric triangle waves.
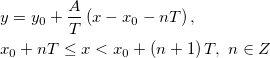
|
| Sine(x,y0,xc,w,A)
|
Sine wave function oscillates around a specified value.
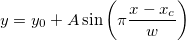
|
| SineDamp(x,y0,xc,w,t0,A)
|
Damped sine wave, a sinusoidal function whose amplitude decays as time increases.
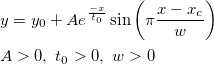
|
| SineSqr(x,y0,xc,w,A)
|
sine square function.
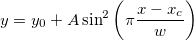
|
| SquareWave(x,a,b,x0,T)
|
Square wave function which is a periodic wave changing between two levels transitionally.
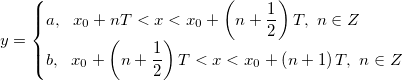
|
| SquareWaveMod(x, a, b, x0, duty, T)
(2016 SR0)
|
Modified square wave function with duty cycle which is a periodic wave changing between two levels transitionally.
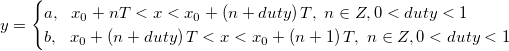
|
| Step(x,A,B,x1)
|
Piecewise constant function with two segments.
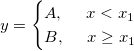
|
Surface Fitting
| Name
|
Brief Description
|
| Chebyshev2D(x,y,z0,A1,A2,B1,B2,C1)
|
Chebyshev Series Polynomials.
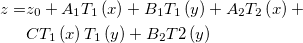
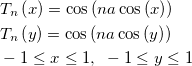
|
| Cosine(x,y,z0,A1,A2,B1,B2,C1)
|
Cosine Series Polynomials.
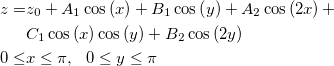
|
| DoseResp2D(x,y,z0,B,C,D,E,F)
|
Non-Linear Logistic Dose Response Function.
![z=z_0+\frac B{\left[ 1+\left( \frac xC\right) ^{-D}\right] \left[ 1+\left( \frac yE\right) ^{-F}\right] } z=z_0+\frac B{\left[ 1+\left( \frac xC\right) ^{-D}\right] \left[ 1+\left( \frac yE\right) ^{-F}\right] }](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-f62653f29cbc689e720bbe0fe5cbadb4.png?v=0)
|
| Exponential2D(x,y,z0,B,C,D)
|
2D exponential decay function.
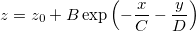
|
| Extreme2D(x,y,z0,B,C,D,E,F)
|
Non-Linear Extreme Value Functions.
![\begin{aligned}z=&z_0+By+Cy^2+D\exp \Bigg[ 1-\exp \left( \frac{E-x}F\right) -\\
&\frac{x-E}F\Bigg] \end{aligned} \begin{aligned}z=&z_0+By+Cy^2+D\exp \Bigg[ 1-\exp \left( \frac{E-x}F\right) -\\
&\frac{x-E}F\Bigg] \end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-a0c9ce975318fafdf4138b076211c01e.png?v=0)
|
| ExtremeCum(x,y,z0,B,C,D,E,F,G,H)
|
Non-Linear Extreme Value Cumulative Function.
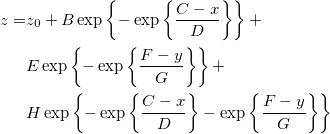
|
| Fourier2D(x,y,z0,a,b,c,d,w1,w2)
|
Sum of sine and cosine functions of two variables.
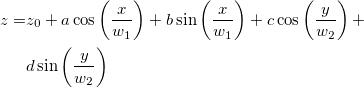
|
| Gauss2D(x,y,z0,A,xc,w1,yc,w2)
|
The Gaussian surface.
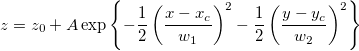
|
| GaussCum(x,y,z0,B,C,D,E,F)
|
2D Gaussian cumulative function.
![\begin{aligned}z=&z_0+0.25B\left[1+{erf}\left\{\frac{x-C}{\sqrt{2}D}\right\}\right]\bigg[1+\\
&{erf}\left\{\frac{y-E}{\sqrt{2}F}\right\}\bigg]\end{aligned} \begin{aligned}z=&z_0+0.25B\left[1+{erf}\left\{\frac{x-C}{\sqrt{2}D}\right\}\right]\bigg[1+\\
&{erf}\left\{\frac{y-E}{\sqrt{2}F}\right\}\bigg]\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-720208e859a9ac6fb5b01b06e95e8197.png?v=0)
|
| Gaussian2D(x,y,z0,A,xc,w1,yc,w2,theta)
|
The gaussian surface rotated.
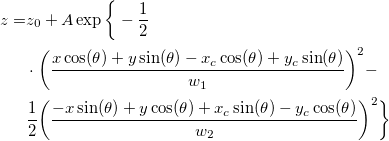
|
| LogisticCum(x,y,z0,B,C,D,E,F)
|
Non-linear Sigmoid (Logistic Cumulative) Function.
![z=z_0+\frac B{\left[ 1+\exp \left\{ \frac{C-x}D\right\} \right] \big[ 1+\exp \big\{ \frac{E-y}F\big\} \big] } z=z_0+\frac B{\left[ 1+\exp \left\{ \frac{C-x}D\right\} \right] \big[ 1+\exp \big\{ \frac{E-y}F\big\} \big] }](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-32a77cf59f1fefd1e2ce0e84f3bf73fe.png?v=0)
|
| LogNormal2D(x,y,z0,B,C,D,E,F,G,H)
|
2D Log Normal function.
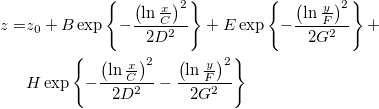
|
| Lorentz2D(x,y,z0,A,xc,w1,yc,w2)
|
Non-linear Sigmoid (Logistic Cumulative) Function.
![z=z_0+\frac A{\left[ 1+\left( \frac{x-x_c}{w_1}\right) ^2\right] \left[ 1+\left( \frac{y-y_c}{w_2}\right) ^2\right] } z=z_0+\frac A{\left[ 1+\left( \frac{x-x_c}{w_1}\right) ^2\right] \left[ 1+\left( \frac{y-y_c}{w_2}\right) ^2\right] }](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-285d961d27715d22e87d343a2be517aa.png?v=0)
|
| Parabola2D(x,y,z0,a,b,c,d)
|
2D Parabola function without xy term.
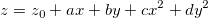
|
| Plane(x,y,z0,a,b)
|
The Plane Surface.
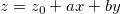
|
| Poly2D(x,y,z0,a,b,c,d,f)
|
2D quadratic polynomial.
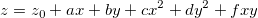
|
| Polynomial2D(x,y,z0,A1,A2,A3,A4,A5,B1,B2,B3,B4,B5)
|
2D 5th order polynomial without cross terms.
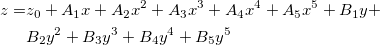
|
| Power2D(x,y,z0,B,C,D,E,F)
|
2D power function.
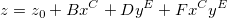
|
| Rational2D(x,y,z0,A01,B01,B02,B03,A1,A2,A3,B1,B2)
|
2D rational function with 3rd order for numerator and 3rd order for denominator.
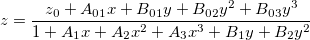
|
| RationalTaylor(x,y,z0,A01,B01,B02,C02,A1,A2,B1,B2,C2)
|
2D Taylor series rational function.
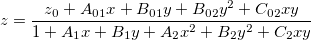
|
| Voigt2D(x,y,z0,A,xc,w1,yc,w2,mu)
|
The Voigt surface.
![\begin{aligned}z=&z_0+A\Bigg[\frac{\mu\!}{\left[1+\left(\frac{x-x_c}{w_1}\right)^2\right]\left[1+\left(\frac{y-y_c}{w_2}\right)^2\right]}
+\\
&(1-\mu\!)\exp\left(-\frac{1}{2}\left(\frac{x-x_c}{w_1}\right)^2-\frac{1}{2}\left(\frac{y-y_c}{w_2}\right)^2\right)\Bigg]\end{aligned} \begin{aligned}z=&z_0+A\Bigg[\frac{\mu\!}{\left[1+\left(\frac{x-x_c}{w_1}\right)^2\right]\left[1+\left(\frac{y-y_c}{w_2}\right)^2\right]}
+\\
&(1-\mu\!)\exp\left(-\frac{1}{2}\left(\frac{x-x_c}{w_1}\right)^2-\frac{1}{2}\left(\frac{y-y_c}{w_2}\right)^2\right)\Bigg]\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-4dc3ec1c5687631274f03b0d75c247b4.png?v=0)
|
| Voigt2DMod(x,y,z0,A,xc,w1,yc,w2,mu)
(2016 SR0)
|
The voigt surface with volume as parameter.
![\begin{aligned}z=&z0+A\Bigg[\frac{mu}{(1+((x-xc)/w1)^2)*(1+((y-yc)/w2)^2)}
+\\
&(1-mu)*exp(-\frac{1}{2}*(\frac{x-xc}{w1})^2-\frac{1}{2}*(\frac{y-yc}{w2})^2)\Bigg]\end{aligned} \begin{aligned}z=&z0+A\Bigg[\frac{mu}{(1+((x-xc)/w1)^2)*(1+((y-yc)/w2)^2)}
+\\
&(1-mu)*exp(-\frac{1}{2}*(\frac{x-xc}{w1})^2-\frac{1}{2}*(\frac{y-yc}{w2})^2)\Bigg]\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-1255c4dc06f394fbd52ac23a2d40c4cb.png?v=0)
|
PFW
| Name
|
Brief Description
|
| Asym2Sig(x,y0,xc,A,w1,w2,w3)
|
Asymmetric double Sigmoidal function.
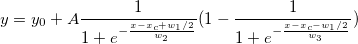
|
| Bigaussian(x,y0,xc,H,w1,w2)
|
Bi-Gaussian peak function used to fit asymmetric peak.
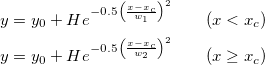
|
| BWF(x,y0,xc,H,w,q)
|
Breit-Wigner-Fano (BWF) line shape.
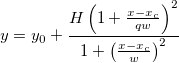
|
| CCE(x,y0,xc1,A,w,k2,xc2,B,k3,xc3)
|
Chesler-Cram Peak Function for use in chromatography.
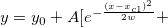
![B(1-0.5(1-\tanh (k_2(x-x_{c2}))))e^{-0.5k_3(|x-x_{c3}|+(x-x_{c3}))}] B(1-0.5(1-\tanh (k_2(x-x_{c2}))))e^{-0.5k_3(|x-x_{c3}|+(x-x_{c3}))}]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-57b6cef7f7567fd6ee984db95247d48c.png?v=0)
|
| ConsGaussian(x,y0, xc, A, w1, w2)
|
Constrained Gaussian function.
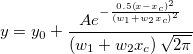
|
| DoniachSunjic(x,y0, xc, H, w, a)
|
Doniach Sunjic function.
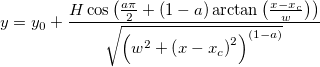
|
| ECS(x,y0,xc,A,w,a3,a4)
|
Edgeworth-Cramer Peak Function for use in chromatography.
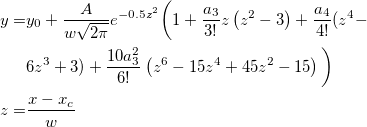
|
| FraserSuzuki(x,y0,xc,A,sig)
|
Fraser-Suzuki asymmetric function.
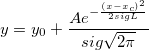 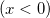
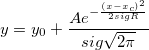 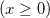
Where
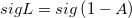 , ,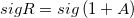
|
| Gauss(x, y0, xc, w, A)
|
Area version of Gaussian Function.
(y0 = offset, xc = center, w = width, A = area)
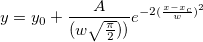
|
| GaussAmp(x,y0,xc,w,A)
|
Amplitude version of Gaussian peak function.
(y0 = offset, xc = center, w = width, A = amplitude)
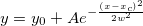
|
| Gaussian(x,y0,xc,A,w)
|
FWHM version of Gaussian Function.
(y0 = base, xc = center, A = area, w = FWHM)
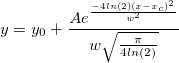
|
| Gaussian_LorenCross(x,y0, xc, A, w, s)
|
Gaussian-Lorentzian Cross Product function.

|
| GaussMod(x,y0,A,xc,w,t0)
|
Exponentially modified Gaussian (EMG) peak function for use in Chromatography.
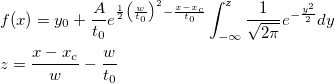
|
| GCAS(x,y0,xc,A,w,a3,a4)
|
Gram-Charlier peak function for use in chromatography.

|
| HVL(x, y0, xc, A, w, d)
|
Haaroff-Van der Linde function.
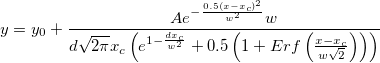
|
| InvsPoly(x,y0,xc,w,A,A1,A2,A3)
|
Inverse polynomial peak function with center.
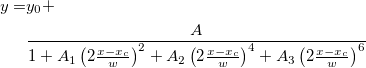
|
| LogNormal(x,y0,xc,w,A)
|
Probability density function of random variable whose logarithm is normally distributed.
![y=y_0+\frac A{\sqrt{2\pi }wx}e^{\frac{-\left[ \ln \frac x{xc}\right] ^2}{2w^2}} y=y_0+\frac A{\sqrt{2\pi }wx}e^{\frac{-\left[ \ln \frac x{xc}\right] ^2}{2w^2}}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-e98dcb616116ac2349df7544a55b124f.png?v=0)
|
| Lorentz(x, y0, xc, w, A)
|
Lorentzian peak function with bell shape and much wider tails than Gaussian function.
(y0 = offset, xc = center, w = FWHM, A = area)
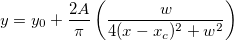
|
| PearsonVII(x,y0,xc,A,w,m)
|
Pearson Type VII peak function is a Lorentz function raised to a power.
![\begin{aligned}&y=y_0+A\frac{2\Gamma (\mu)\sqrt{2^{\frac{1}{\mu}}-1}}{\sqrt{\pi }\Gamma \left( \mu-\frac 12\right) w}\bigg[ 1+4\frac{2^{\frac{1}{\mu}}-1}{w^2}\left( x-x_c\right) ^2\bigg] ^{-\mu}\\
&m=\mu\end{aligned} \begin{aligned}&y=y_0+A\frac{2\Gamma (\mu)\sqrt{2^{\frac{1}{\mu}}-1}}{\sqrt{\pi }\Gamma \left( \mu-\frac 12\right) w}\bigg[ 1+4\frac{2^{\frac{1}{\mu}}-1}{w^2}\left( x-x_c\right) ^2\bigg] ^{-\mu}\\
&m=\mu\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-3dfdbeab0848b14621c0b803f539eb3b.png?v=0)
|
| PsdVoigt1(x,y0,xc,A,w,mu)
|
Pseudo-Voigt function, linear combination of Gaussian function and Lorentzian function.
(y0 = offset, xc = center, A = area, w = FWHM, mu = profile shape factor)
![\begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac w{4\left( x-x_c\right) ^2+w^2}\\
&+\left( 1-m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w}e^{-\frac{4\ln 2}{w^2}\left( x-x_c\right) ^2}\bigg]\end{aligned} \begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac w{4\left( x-x_c\right) ^2+w^2}\\
&+\left( 1-m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w}e^{-\frac{4\ln 2}{w^2}\left( x-x_c\right) ^2}\bigg]\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-a2bbe7b2678afc56a46e94e4092a69a5.png?v=0)
|
| PsdVoigt2(x,y0,xc,A,wG,wL,mu)
|
Pseudo-Voigt function, linear combination of Gaussian and Lorentzian with different FWHM.
(y0 = offset, xc = center, A =area, wG=Gaussian FWHM, wL=Lorentzian FWHM, mu = profile shape factor)
![\begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac{w_L}{4\left( x-x_c\right) ^2+w_L^2}+\\
&\left( 1-m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w_G}e^{-\frac{4\ln 2}{w_G^2}\left( x-x_c\right) ^2}\bigg] \end{aligned} \begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac{w_L}{4\left( x-x_c\right) ^2+w_L^2}+\\
&\left( 1-m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w_G}e^{-\frac{4\ln 2}{w_G^2}\left( x-x_c\right) ^2}\bigg] \end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-a7026ad226684f46e4581ae2a80929b1.png?v=0)
|
| Pulse(x,y0,x0,A,t1,P,t2)
|
Exponential pulse function(x >= x0 ? y : 0).
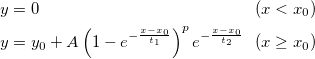
|
| SchulzFlory(x,y0,xc,w,A)
|
Schulz Flory distribution function to describe relative ratios of polymers after a polymerization process.
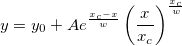
|
| Sine(x,xc,w,A,y0)
|
Sine wave function oscillates around a specified value.
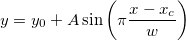
|
| SineDamp(x,y0,xc,w,t0,A)
|
Damped sine wave, a sinusoidal function whose amplitude decays as time increases.
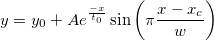
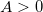 , , 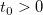 , , 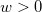
|
| Sinesqr(x,xc,w,A,y0)
|
sine square function.
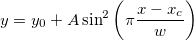
|
| Voigt(x,y0,xc,A,wG,wL)
|
Convolution of a Gaussian function (wG for FWHM) and a Lorentzian function.
(y0 = offset, xc = center, A =area, wG = Gaussian FWHM, wL = Lorentzian FWHM)
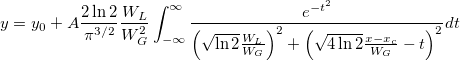
|
| Weibull3(x,y0,xc,A,w1,w2)
|
Amplitude version of Weibull peak function.
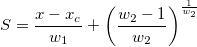
![y=y_0+A\left( \frac{w_2-1}{w_2}\right) ^{\frac{1-w_2}{w_2}}\left[ S\right] ^{w_2-1}e^{-\left[ S\right] ^{w_2}+\left( \frac{w_2-1}{w_2}\right) } y=y_0+A\left( \frac{w_2-1}{w_2}\right) ^{\frac{1-w_2}{w_2}}\left[ S\right] ^{w_2-1}e^{-\left[ S\right] ^{w_2}+\left( \frac{w_2-1}{w_2}\right) }](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-2566aad3afe36e3faadff13e4072dcd8.png?v=0)
|
Baseline
| Name
|
Brief Description
|
| Constant(x,y0)
|
Constant base line function.
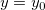
|
| Cubic(x,A,B,C,D)
|
Third order polynomial.
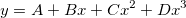
|
| ExpDec1(x,y0,A1,t1)
|
One-phase exponential decay function with time constant parameter.
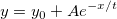
|
| ExpDec2(x,y0,A1,t1,A2,t2)
|
Two-phase exponential decay function with time constant parameters.
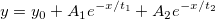
|
| ExpGro1(x,y0,A1,t1)
|
One-phase exponential growth function with time constant parameter.
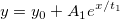
|
| ExpGrow1(x,y0,x0,A1,t1)
|
One-phase exponential growth with time offset, x0 should be fixed.
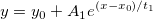
|
| ExpGrow2(x, y0, x0, A1, t1, A2, t2)
|
Two-phase exponential growth with time offset, x0 should be fixed.
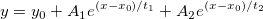
|
| Exponential(x,y0,A,R0)
|
Exponential growth function with rate constant parameter.
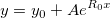
|
| Hyperbl(x, P1, P2)
|
Hyperbola funciton, also the Michaelis-Menten model in Enzyme Kinetics.
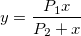
|
| Line(x,A,B)
|
Line function with slope and intercept.
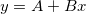
|
| MnMolecular(x,A,xc,k),
|
Monomolecular growth model.
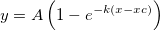
|
| Parabola(x,A,B,C)
|
Second order polynomial.
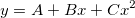
|
| Poly4(x,A0,A1,A2,A3,A4)
|
4th order Polynomial function.
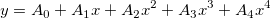
|
| Poly5(x,A0,A1,A2,A3,A4,A5)
|
5th order polynomial function.
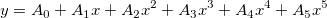
|
| Step(x,A,B,x1)
|
Piecewise constant function with two segments.
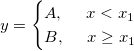
|
Chromatograph
| Name
|
Brief Description
|
| CCE(x,y0,xc1,A,w,k2,xc2,B,k3,xc3)
|
Chesler-Cram Peak Function for use in chromatography.
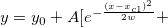
![B(1-0.5(1-\tanh (k_2(x-x_{c2}))))e^{-0.5k_3(|x-x_{c3}|+(x-x_{c3}))}] B(1-0.5(1-\tanh (k_2(x-x_{c2}))))e^{-0.5k_3(|x-x_{c3}|+(x-x_{c3}))}]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-57b6cef7f7567fd6ee984db95247d48c.png?v=0)
|
| ECS(x,y0,xc,A,w,a3,a4)
|
Edgeworth-Cramer Peak Function for use in chromatography.
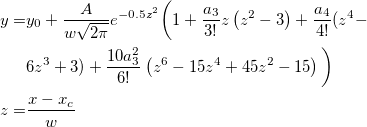
|
| Gauss(x, y0, xc, w, A)
|
Area version of Gaussian Function.
(y0 = offset, xc = center, w = width, A = area)
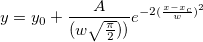
|
| GaussMod(x,y0,A,xc,w,t0)
|
Exponentially modified Gaussian (EMG) peak function for use in Chromatography.
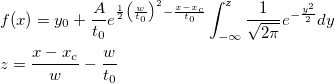
|
| GCAS(x,y0,xc,A,w,a3,a4)
|
Gram-Charlier peak function for use in chromatography.

|
| Giddings(x,y0,xc,w,A)
|
Giddings peak function for use in Chromatography.
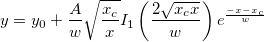
|
Electrophysiology
| Name
|
Brief Description
|
| BoltzIV(x,vhalf,dx,gmax,vrev)
|
Transformed Boltzmann function for IV data.
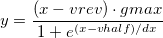
|
| Boltzmann(x, A1, A2, x0, dx)
|
Boltzmann Function - produce a sigmoidal curve.
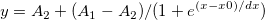
|
| DoubleBoltzmann(x,y0,A,frac,x01,x02,k1,k2)
|
Double Boltzmann Function, sum of two Boltzmann functions.
![y=y_0+A\left[\frac{p}{1+e^{\frac{x-x_{01}}{k_1}}}+\frac{1-p}{1+e^{\frac{x-x_{02}}{k_2}}}\right] y=y_0+A\left[\frac{p}{1+e^{\frac{x-x_{01}}{k_1}}}+\frac{1-p}{1+e^{\frac{x-x_{02}}{k_2}}}\right]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-649e5dcc558a3cbe663ecabcca96fc0e.png?v=0)
|
| ExpDec1(x,y0,A1,t1)
|
One-phase exponential decay function with time constant parameter.
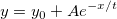
|
| ExpDec2(x,y0,A1,t1,A2,t2)
|
Two-phase exponential decay function with time constant parameters.
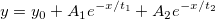
|
| ExpDec3(x,y0,A1,t1,A2,t2,A3,t3)
|
Three-phase exponential decay function with time constant parameters.
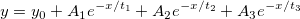
|
| Gauss(x, y0, xc, w, A)
|
Area version of Gaussian Function.
(y0 = offset, xc = center, w = width, A = area)
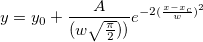
|
| Goldman(x,b,Nao,Nai,Ki,T)
|
Goldman-Hodgkin-Katz equation for use in cell membrane physiology.
![\begin{aligned}&E=\frac{RT}F\ln \left( \frac{\left[ K\right] _0+b\left[ Na\right] _0}{\left[ K\right] _i+b\left[ Na\right] _i}\right)\\
&x=\left[ K\right] _0,~ y=E\\
&R=8.314,F=96485,b=P_k/P_{Na}\end{aligned} \begin{aligned}&E=\frac{RT}F\ln \left( \frac{\left[ K\right] _0+b\left[ Na\right] _0}{\left[ K\right] _i+b\left[ Na\right] _i}\right)\\
&x=\left[ K\right] _0,~ y=E\\
&R=8.314,F=96485,b=P_k/P_{Na}\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-4348b72101a80ee8c917fa817441cee7.png?v=0)
|
| Hill(x,Vmax,k,n)
|
Hill function to determine ligand concentration and maximum number of binding sites.
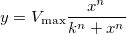
|
Pharmacology
| Name
|
Brief Description
|
| BiDoseResp(x,A1,A2,LOGx01,LOGx02,h1,h2,p)
|
Biphasic Dose Response Function.
![\begin{aligned}y=&A_1+(A_2-A_1)\bigg[\frac{p}{1+10^{(LOGx01-x)h1}}+\\
&\frac{1-p}{1+10^{(LOGx02-x)h2}}\bigg]\end{aligned} \begin{aligned}y=&A_1+(A_2-A_1)\bigg[\frac{p}{1+10^{(LOGx01-x)h1}}+\\
&\frac{1-p}{1+10^{(LOGx02-x)h2}}\bigg]\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-5a931673f336d3539f282df4fd1d9752.png?v=0)
|
| Biphasic(x,Amin,Amax1,Amax2,x0_1,x0_2,h1,h2)
|
Biphasic sigmoidal dose response (7 parameters logistic equation).
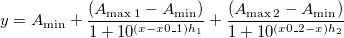
|
| DoseResp(x,A1,A2,LOGx0,p)
|
Dose-response curve with variable Hill slope given by parameter 'p'.
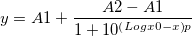
|
| MichaelisMenten(x,Vmax,Km)
|
Michaelis Menten function to describe relation of concentration of substrate and enzyme velocity.
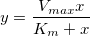
|
| OneSiteBind(x,Bmax,k1)
|
One site direct binding. Rectangular hyperbola, connects to isotherm or saturation curve.
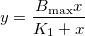
|
| OneSiteComp(x,A1,A2,logx0)
|
One Site Competition curve. Dose-response curve with Hill slope equal to -1.
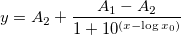
|
| TwoSiteBind(x,Bmax1,Bmax2,k1,k2)
|
Two sites binding function.
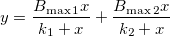
|
| TwoSiteComp(x,A1,A2,logx0_1,logx0_2,fraction)
|
Two sites competition function to describe the competition of a ligand for two types of receptors.
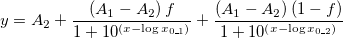
|
Rheology
| Name
|
Brief Description
|
| Bingham(x,y0,A)
(2015 SR0)
|
Bingham model to describe viscoplastic fluids exhibiting a yield response.
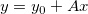
|
| Cross(x,A1,A2,t,m)
(2015 SR0)
|
Cross model to describe pseudoplastic flow with asymptotic viscosities at zero and infinite shear rates.
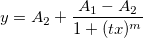
|
| Carreau(x,A1,A2,t,a,n)
(2015 SR0)
|
Carreau-Yasuda model to describe pseudoplastic flow with asymptotic viscosities at zero and infinite shear rates.
![y=A_{2}+(A_{1}-A_{2})[1+(tx)^{a}]^{\frac{n-1}{a}} y=A_{2}+(A_{1}-A_{2})[1+(tx)^{a}]^{\frac{n-1}{a}}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-2a5e177df5333db67ca1608b920108fd.png?v=0)
|
| Herschel(x,y0,K,n)
(2015 SR0)
|
Herschel-Bulkley model to describe viscoplastic materials exhibiting a power-law relationship.
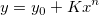
|
| VFT(x,A,B,x0)
(2015 SR0)
|
Vogel-Fulcher-Tammann Equation.
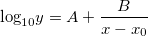
|
| MYEGA(x,y0,K,C)
(2015 SR0)
|
Mauro-Yue-Ellison-Gupta-Allan Equation.
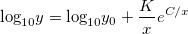
|
Enzyme Kinetics
| Name
|
Brief Description
|
| CompInhib(x,Vmax,Km,Ki,Ic)
(2015 SR0)
|
Competitive inhibition model for single substrate and single inhibitor.
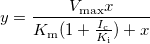
Note that this function is usually used in global fit, Vmax, Km and Ki should be shared, and Ic should be fixed for each dataset. The initial value of Ki can be the mean of Ic.
|
| NoncompInhib(x,Vmax,Km,Ki,Ic)
(2015 SR0)
|
Noncompetitive inhibition model for single substrate and single inhibitor.
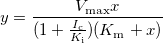
Note that this function is usually used in global fit, Vmax, Km and Ki should be shared, and Ic should be fixed for each dataset. The initial value of Ki can be the mean of Ic.
|
| UncompInhib(x,Vmax,Km,Kia,Ic)
(2015 SR0)
|
Uncompetitive inhibition model for single substrate and single inhibitor.
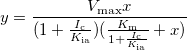
Note that this function is usually used in global fit, Vmax, Km and Kia should be shared, and Ic should be fixed for each dataset. The initial value of Kia can be the mean of Ic.
|
| MixedModelInhib(x,Vmax,Km,Ki,Alpha,Ic)
(2015 SR0)
|
A general equation including competitive, uncompetitive and noncompetitive inhibition as special cases.
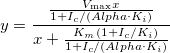
This fitting function is for global fitting. When using it, Vmax, Km, Ki, and Alpha are shared, while Ic is a fixed constant. The initial value of Ki can be the mean of Ic.
|
| SubstrateInhib(x,Vmax,Km,Ki)
(2015 SR0)
|
Substrate inhibition model at high concentrations.
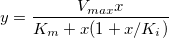
|
| MichaelisMenten(x,Vmax,Km)
|
Michaelis Menten function to describe relation of concentration of substrate and enzyme velocity.
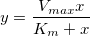
|
| Hill(x,Vmax,k,n)
|
Hill function to determine ligand concentration and maximum number of binding sites.
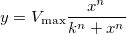
|
Spectroscopy
| Name
|
Brief Description
|
| GaussAmp(x,y0,xc,w,A)
|
Amplitude version of Gaussian peak function.
(y0 = offset, xc = center, w = width, A = amplitude)
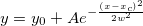
|
| InvsPoly(x,y0,xc,w,A,A1,A2,A3)
|
Inverse polynomial peak function with center.
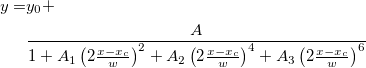
|
| Lorentz(x, y0, xc, w, A)
|
Lorentzian peak function with bell shape and much wider tails than Gaussian function.
(y0 = offset, xc = center, w = FWHM, A = area)
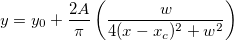
|
| PearsonVII(x,y0,xc,A,w,m)
|
Pearson Type VII peak function is a Lorentz function raised to a power.
![\begin{aligned}&y=y_0+A\frac{2\Gamma (\mu)\sqrt{2^{\frac{1}{\mu}}-1}}{\sqrt{\pi }\Gamma \left( \mu-\frac 12\right) w}\bigg[ 1+4\frac{2^{\frac{1}{\mu}}-1}{w^2}\left( x-x_c\right) ^2\bigg] ^{-\mu}\\
&m=\mu\end{aligned} \begin{aligned}&y=y_0+A\frac{2\Gamma (\mu)\sqrt{2^{\frac{1}{\mu}}-1}}{\sqrt{\pi }\Gamma \left( \mu-\frac 12\right) w}\bigg[ 1+4\frac{2^{\frac{1}{\mu}}-1}{w^2}\left( x-x_c\right) ^2\bigg] ^{-\mu}\\
&m=\mu\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-3dfdbeab0848b14621c0b803f539eb3b.png?v=0)
|
| PsdVoigt1(x,y0,xc,A,w,mu)
|
Pseudo-Voigt function, linear combination of Gaussian function and Lorentzian function.
(y0 = offset, xc = center, A = area, w = FWHM, mu = profile shape factor)
![\begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac w{4\left( x-x_c\right) ^2+w^2}+\\
&\left( 1- m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w}e^{-\frac{4\ln 2}{w^2}\left( x-x_c\right) ^2}\bigg] \end{aligned} \begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac w{4\left( x-x_c\right) ^2+w^2}+\\
&\left( 1- m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w}e^{-\frac{4\ln 2}{w^2}\left( x-x_c\right) ^2}\bigg] \end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-054a79b30e4c7feda522b89c192979bc.png?v=0)
|
| PsdVoigt2(x,y0,xc,A,wG,wL,mu)
|
Pseudo-Voigt function, linear combination of Gaussian and Lorentzian with different FWHM.
(y0 = offset, xc = center, A =area, wG=Gaussian FWHM, wL=Lorentzian FWHM, mu = profile shape factor)
![\begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac{w_L}{4\left( x-x_c\right) ^2+w_L^2}+\\
&\left( 1-m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w_G}e^{-\frac{4\ln 2}{w_G^2}\left( x-x_c\right) ^2}\bigg]\end{aligned} \begin{aligned}y=&y_0+A\bigg[ m_u\frac 2\pi \frac{w_L}{4\left( x-x_c\right) ^2+w_L^2}+\\
&\left( 1-m_u\right) \frac{\sqrt{4\ln 2}}{\sqrt{\pi}w_G}e^{-\frac{4\ln 2}{w_G^2}\left( x-x_c\right) ^2}\bigg]\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-c222b784c08a7133e8cd95fac7d804fa.png?v=0)
|
| Voigt(x,y0,xc,A,wG,wL)
|
Convolution of a Gaussian function (wG for FWHM) and a Lorentzian function
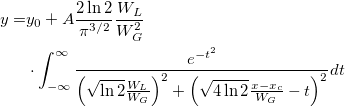
|
Statistics
| Name
|
Brief Description
|
| Exponential(x,y0,A,R0)
|
Exponential growth function with rate constant parameter.
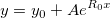
|
| ExponentialCDF(x,y0,A,mu)
(2016 SR0)
|
Exponential cumulative distribution function.
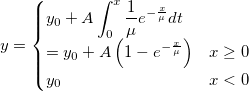
|
| Extreme(x,y0,xc,w,A)
|
Particular case of extreme function, Gumbel probability density function.
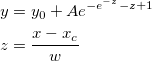
|
| GammaCDF(x,y0,A1,a,b)
(2016 SR0)
|
Gamma cumulative distribution function.
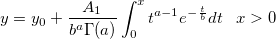
|
| Gauss(x, y0, xc, w, A)
|
Area version of Gaussian Function.
(y0 = offset, xc = center, w = width, A = area)
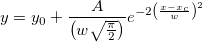
|
| GaussAmp(x,y0,xc,w,A)
|
Amplitude version of Gaussian peak function.
(y0 = offset, xc = center, w = width, A = amplitude)
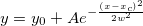
|
| Gumbel(x,a,b)
|
Transformed Gumbel cumulative distribution function.
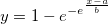
|
| Laplace(x,y0,a,b)
|
Laplace probability density function.
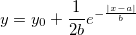
|
| Logistic(x, A1, A2, x0, p)
|
Logistic dose response in Pharmacology/Chemistry. Also known as 4PL or 4PLC.
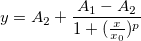
|
| LogNormal(x,y0,xc,w,A)
|
Probability density function of random variable whose logarithm is normally distributed.
![y=y_0+\frac A{\sqrt{2\pi }wx}e^{\frac{-\left[ \ln \frac x{x_c}\right] ^2}{2w^2}} y=y_0+\frac A{\sqrt{2\pi }wx}e^{\frac{-\left[ \ln \frac x{x_c}\right] ^2}{2w^2}}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-3220dc36e6a1075cbff267293aa3febe.png?v=0)
|
| LognormalCDF(x,y0,A,xc,w)
(2016 SR0)
|
LognormalCDF cumulative distribution function.
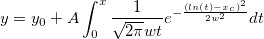
|
| Lorentz(x, y0, xc, w, A)
|
Lorentzian peak function with bell shape and much wider tails than Gaussian function.
(y0 = offset, xc = center, w = FWHM, A = area)
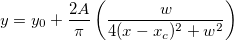
|
| NormalCDF(x,y0,A,xc,w)
|
Normal cumulative distribution function.
( y0 = offset, A = Amplitude, xc = Mean, w = Standard Deviation)
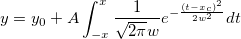
|
| Pareto(x,A)
|
Pareto cumulative distribution function with one parameter, a power law probability distribution.
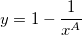
|
| Pareto2(x,a,b)
|
Pareto function with two parameters.
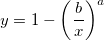
|
| PearsonIV(x,y0,A,m,v,alpha,lam)
|
Pearson Type IV distribution for negative discriminant, suited to model pull distributions.
![\begin{aligned}&y=y_0+Ak\left[1+\left(\frac{x-\lambda\!}{\alpha\!}\right)\right]^{-m}e^{-v\tan^{-1}\left(\frac{x-\lambda\!}{\alpha\!}\right) } \\
&k=\frac{2^{2m-2}|\Gamma\!\left(m+iv/2\right)|^2}{\pi\!\alpha\!\Gamma\!\left(2m-1\right)}, m>\frac{1}{2}\end{aligned} \begin{aligned}&y=y_0+Ak\left[1+\left(\frac{x-\lambda\!}{\alpha\!}\right)\right]^{-m}e^{-v\tan^{-1}\left(\frac{x-\lambda\!}{\alpha\!}\right) } \\
&k=\frac{2^{2m-2}|\Gamma\!\left(m+iv/2\right)|^2}{\pi\!\alpha\!\Gamma\!\left(2m-1\right)}, m>\frac{1}{2}\end{aligned}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/LabTalk/images/LabTalk-Supported_Functions/math-2578f3f3d1060040453114eb42fee3a2.png?v=0)
|
| Poisson(x,y0,r)
|
Poisson probability density function, a discrete probability distribution.
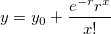
|
| Rayleigh(x,b)
|
Rayleigh cumulative distribution function.
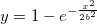
|
| Weibull(x,y0,a,r,u)
|
Weibull probability density function.
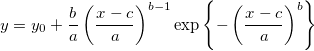
|
| WeibullCDF(x,y0,A1,a,b)
(2016 SR0)
|
Weibull cumulative distribution function.
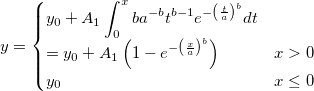
|
Quick Fit
| Name
|
Brief Description
|
| Boltzmann(x, A1, A2, x0, dx)
|
Boltzmann Function - produce a sigmoidal curve.
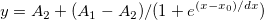
|
| DoseResp(x,A1,A2,LOGx0,p)
|
Dose-response curve with variable Hill slope given by parameter 'p'.
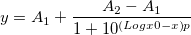
|
| ExpDecay1(x,y0,x0,A1,t1)
|
One-phase exponential decay function with time offset, x0 should be fixed.
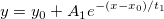
|
| ExpGrow1(x,y0,x0,A1,t1)
|
One-phase exponential growth with time offset, x0 should be fixed.
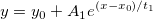
|
| Gauss(x, y0, xc, w, A)
|
Area version of Gaussian Function.
(y0 = offset, xc = center, w = width, A = area)
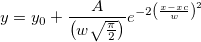
|
| Hill(x,Vmax,k,n)
|
Hill function to determine ligand concentration and maximum number of binding sites.
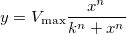
|
| Hyperbl(x, P1, P2)
|
Hyperbola funciton, also the Michaelis-Menten model in Enzyme Kinetics.
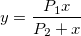
|
| Logistic(x, A1, A2, x0, p)
|
Logistic dose response in Pharmacology/Chemistry. Also known as 4PL or 4PLC.
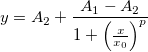
|
| Lorentz(x, y0, xc, w, A)
|
Lorentzian peak function with bell shape and much wider tails than Gaussian function.
(y0 = offset, xc = center, w = FWHM, A = area)
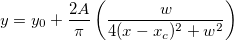
|
| Sine(x,y0,xc,w,A)
|
Sine wave function oscillates around a specified value.
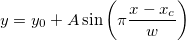
|
| Voigt(x,y0,xc,A,wG,wL)
|
Convolution of a Gaussian function (wG for FWHM) and a Lorentzian function.
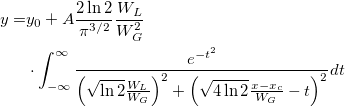
|
Multiple Variables
| Name
|
Brief Description
|
| GaussianLorentz(y0, xc, A1, A2, w1, w2)
|
One independent and two dependent variables, shared parameters.
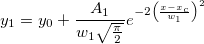
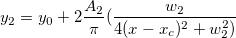
|
| Helix(x,x0,y0,A,w,p)
|
3D Helix Function.
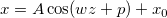
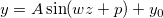
|
| HillBurk(Vm1, Km1, Vm2, Km2)
|
Combination of Hill and Burk models with two independent and two dependent variables.
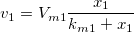
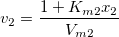
|
| Line3(a, b, c, d)
|
3D Line function with slopes and intercepts.
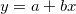
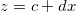
|
| LineExp(x,Vmax,k,n)
|
Combination of Line and Exponential models with one independent and two dependent variables.
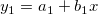
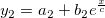
|
Miscellaneous
| Name
|
Brief Description
|
| BitAND(n1, n2)
|
Returns bitwise AND operation of two integers.
|
| BitOR(n1, n2)
|
Returns bitwise OR operation of two integers.
|
| BitXOR(n1, n2)
|
Returns bitwise XOR operation of two integers.
|
| ISNA(d)
|
Determines whether the number is a NANUM.
|
| isText(str$)
(2019)
|
Determine whether a value is a text. Return 1 for text and blank value; return 0 for numeric value or NANUM.
|
| Let(var1,val1[,var2,val2,]...[,var39, val39], expression)[$]
(2021)
|
Similar to MS Excel's LET() function. Assign values (valN) to variables (varN) for up to 39 variable-value pairs, for use in expression. Optional $ used when returning strings. examples:
-
LET(t,if(A$==B$,1,0/0),t*500) returns missing value ("--") if two strings do not match, otherwise "500".
-
LET(first,left(A,1),last,left(B,2), first$+ "-" + last$) concatenate 2 strings with literal "-" separator.
|
| NA()
|
Returns NANUM.
|
| ocolor2rgb(oColor)
(2019 SR0)
|
Convert an internal color code oColor to RGB value.
|
| xf_get_last_error_code()
|
Get the last error code value of XFunction engine.
|
| xf_get_last_error_message()$
|
Get the last error string message of XFunction engine.
|
| xor(n1,n2)
(2019 SR0)
|
Returns XOR operation of two logical values n1 and n2. Example
XOR(1>0,7>2) returns 0 because both TRUEXOR(1<0,7<2) returns 0 because both FALSEXOR(1>0,7<2) returns 1 because 1st TRUE and 2nd FALSE
|
Engineering
| Name
|
Brief Description
|
| Base(num,radix[,len])$
(2019 SR0)
|
Convert a given integer num into a string representation of the specified
radix.
|
| Bin2Dec(str$)
|
Convert a binary number to decimal.
|
| BitLShift(num,shift)
(2019 SR0)
|
Shift a decimal number num left by the specified number of bits shift.
|
| BitRShift(num,shift)
(2019 SR0)
|
Shift a decimal number num right by the specified number of bits shift.
|
| Convert(d,str1$,str2$)
|
Convert a number from one measurement system to another.
|
| Decimal(text$,radix)
|
Convert a string representation text in the specified radix into a
decimal number.
|
| Dec2Bin(n)$
|
Convert a decimal number to binary. The input range is limited to -512 to 511.
|
| Dec2Hex(n[,places])$
|
Convert a decimal number to hexadecimal and optionally, specify number of characters.
|
| Hex2Dec(str$)
|
Convert a string representation of a hexadecimal number to decimal.
|
Complex
| Name
|
Brief Description
|
| Imabs(c)
|
Get the modulus of a complex number.
|
| Imaginary(c)
|
This function is used to get the imaginary part of a complex number.
|
| Imargument(c)
|
Get the argument (theta) of a complex number.
|
| Imatan(c)
(2016 SR0)
|
Calculate the inverse tangent of a complex number.
|
| Imatanh(c)
(2016 SR0)
|
Calculate the inverse hyperbolic tangent of a complex number.
|
| Imconjugate(c)
|
Get the conjugate of a complex number.
|
| Imcos(c)
|
Calculate the cosine value for a complex number.
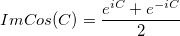
where C is a complex, and 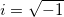 . .
|
| Imcosh(c)
(2019 SR0)
|
Calculate the hyperbolic cosine of a given complex number.
|
| Imcot(c)
(2019 SR0)
|
Calculate the cotangent of a given complex number.
|
| Imcsc(c)
(2019 SR0)
|
Calculate the cosecant of a given complex number.
|
| Imcsch(c)
(2019 SR0)
|
Calculate the hyperbolic cosecant of a given complex number.
|
| Imsec(c)
(2019 SR0)
|
Calculate the secant of a given complex number.
|
| Imsech(c)
(2019 SR0)
|
Calculate the hyperbolic secant of a given complex number.
|
| Imsinh(c)
(2019 SR0)
|
Calculate the hyperbolic sine of a given complex number.
|
| Imtan(c)
(2019 SR0)
|
Calculate the tangent of a given complex number.
|
| Imdiv(c1,c2)
|
Calculate the complex division.
|
| Imexp(c)
|
Calculate the exponential value for a complex number.
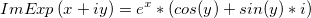
where 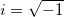 . .
|
| Imln(c)
|
Calculate the natural logarithm of the complex number.
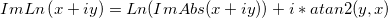
where ImAbs computes the modulus of the complex,
|
| Imlog10(c)
|
Calculate the base 10 logarithm of a complex number.
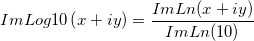
where ImLn computes the natural logarithm of the complex, and 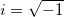 . .
|
| Imlog2(c)
|
Calculate the base 2 logarithm of a complex number.
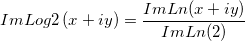
where ImLn computes the natural logarithm of the complex, and 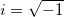 . .
|
| ImPower(c,d)
|
Calculate the given complex to the power of the specified value.
|
| Improduct(c1,c2)
|
Perform the product (multiplication) operation of two complex numbers.
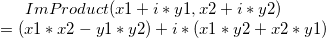
|
| ImReal(c)
|
Get the real part of the specified complex number.
|
| Imsin(c)
|
Calculate the sine value for a complex number.
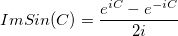
where C is complex, and 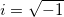 . .
|
| Imsqrt(c)
|
Calculate the square root of a complex number.
|
| ImSub(c1,c2)
|
Perform subtraction between two complex numbers.
|
| ImSum(c1,c2)
|
Get sum of two specified complex numbers.
|
| Real2Complex(real,imag)
|
Convert the specified two reals into a complex number. Note that the data type of output column needs to be set as complex (16) in advance. examples:
-
real2complex(1, 2) returns complex number 1 + 2i
-
real2complex(col(A), col(B)) returns a complex vector, the real part uses values from column A, imaginary part from column B
|
Financial
Notes on Use
Each function returns either a single value or a range of values (a dataset), depending on the type of function and the arguments supplied. Unless otherwise specified, all functions will return a range if the first argument passed to the function is a range, and all functions will return a value if a value is passed.
|