2.13.1.22 swtest
Brief Information
Shapiro-Wilk Normality test
Command Line Usage
1. swtest irng:=col(a)
2. swtest irng:=Col(A) stat:=w df:=d prob:=p
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
irng
|
Input
Range
|
<active>
|
This variable specifies the input data range for test normality. The sample size of data range needs to be between 3 and 5000 for the Shapiro-Wilk test to apply.
|
| Statistics
|
stat
|
Output
double
|
<unassigned>
|
Value of Shapiro-Wilk W statistic. This variable specifies the name of output statistic value.
|
| Degrees of Freedom
|
df
|
Output
double
|
<unassigned>
|
Degrees of freedom of the test. This variable specifies the name of output degrees of freedom value.
|
| P-value
|
prob
|
Output
double
|
<unassigned>
|
Probability that the null hypothesis, i.e. that the data are from normal distribution, will be rejected. This variable specifies the name of output probability value.
|
Description
The Shapiro-Wilk Normality Test is used to determine whether or not a random sample of values follows a normal distribution. The normality test is useful because other statistical tests (such as the t-test, 1- and 2-way ANOVA) require that data be sampled from a normally distributed population in order to produce statistically significant results. A W statistic and a p value are computed, which can be compared with a chosen level of significance, and used to make a statistical decision.
Examples
1. To list all input and output results of Shapiro-Wilk test on the 1st column of the active worksheet, using default setting, type:
- swtest irng:=col(a);
- swtest.=
2. To return the Shapiro-Wilk test statistic for the 2nd column of active worksheet, and test to see if these sample data arise from a normal distribution, type:
- swtest irng:=col(b) stat:=s;
Algorithm
This routine calculates Shapiro Wilk's W statistic with a given significance level for any sample size between 3 and 5000. Origin calculates the W statistic based on the Applied Statistics Algorithm R94. The full description of the theory behind this algorithm is given in Royston (1995).
Given a set of observations 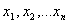 sorted into either ascending or descending order, the Shapiro Wilk W statistic is defined as: sorted into either ascending or descending order, the Shapiro Wilk W statistic is defined as:
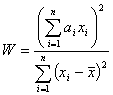
where 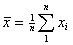 is the sample mean and is the sample mean and  , for , for 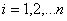 are a set of mathematical weights, the values of which depend only on the sample size n. are a set of mathematical weights, the values of which depend only on the sample size n.
References
Royston JP. AS R94. 1995. Shapiro-Wilk normality test and P-value. Applied Statistics; 44(4).
Related X-Functions
stats, kstest, lillietest
Keywords:normal distribution
|