2.8.16 interpxyz
Menu Information
Analysis: Mathematics: XYZ Trace Interpolation
Brief Information
Perform trace/periodic interpolation on the XYZ data
Additional Information
Minimum Origin Version Required:8.5 SR0
Command Line Usage
interpxyz iz:=Col(3) method:=linear npts:=50;
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
iz
|
Input
XYZRange
|
<active>
|
The input XYZ data range to be interpolated.
|
| Method
|
method
|
Input
Int
|
<0>
|
The method used to interpolate.
Option list:
- linear:Linear
- Use linear interpolation method.
- spline:Cubic Spline
- Use cubic spline interpolation method.
- bspline:Cubic B-Spline
- Use cubic B-spline interpolation method.
|
| Number of Points
|
npts
|
Input
int
|
<10>
|
Specifies the number of data points in the the interpolated data set.
|
| Output
|
oz
|
Output
XYZRange
|
<new>
|
Specifies the destination of the interpolated data.
See the syntax here.
|
Description
This X-Function performs interpolation on XYZ data. The interpolation methods include Linear, Cubic Spline, and Cubic B-spline.
Examples
- Import Interpolation.dat, which is in the <Origin Installation Directory>\Samples\Mathematics\ folder.
- Highlight Column C and set the column designation to Z. Then select Analysis: Mathematics: XYZ Trace Interpolation from the Origin menu to bring up the dialog.
- Note that the Input branch has been filled with the proper data range. Then select the Cubic Spline interpolation method.
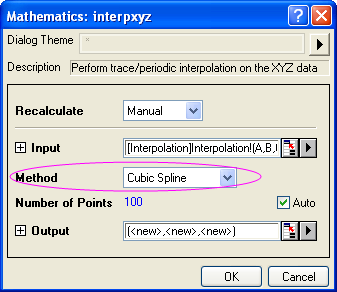
- Click OK to perform the interpolation.
Algorithm
In general, between two adjacent data points, the data points will be interpolated so that the number of data points in the final result data set will be equal to the Number of Points variable.
The detailed algorithm is described below:
Given a sequence of distinct triplets of data (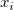 , , 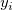 , ,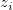 ), where i = 0, 1, ... n-1: ), where i = 0, 1, ... n-1:
For 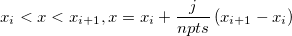 , ,
For 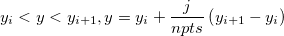 , ,
For 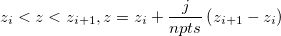 , ,
where j=1,2,3...(npts-1), and npts is the value of Number of Points.
Related X-Functions
interp1, interp1xy, spline, bspline, interp1q, interp2, interp1trace
Keywords:interpolate
|