Theorie der nichtlinearen Kurvenanpassung
NLFit-Theory
So passt Origin eine Linie an
Das Ziel der nichtlinearen Anpassung ist es, die Parameterwerte abzuschätzen, die die Daten am besten beschreiben. Allgemein können wir den Prozess der nichtlinearen Kurvenanpassung wie unten beschreiben.
- Erzeugen Sie eine Anfangsfunktionskurve aus den Initialisierungswerten.
- Führen Sie eine Iteration durch, um die Parameterwerte anzupassen, so dass die Datenpunkte näher an der Kurve liegen.
- Hören Sie auf, wenn die minimale Distanz das Stopp-Kriterium erreicht, um die beste Anpassung zu erhalten.
Origin enthält Optionen für verschiedene Algorithmen, die unterschiedliche iterative Prozeduren und Statistiken haben, um die minimale Distanz zu definieren.
Explizite Funktionen
Anpassungsmodell
Ein allgemeines nichtlineares Modell kann wie folgt ausgedrückt werden:
wobei 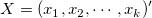 die unabhängige Variable und die unabhängige Variable und 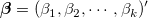 der Parameter ist. der Parameter ist.
 |
Beispiele für die explizite Funktion
|
Algorithmen der kleinsten Quadrate
Der Algorithmus der kleinsten Quadrate besteht darin, die Parameter zu wählen, die die Abweichungen der theoretischen Kurve(n) von den experimentellen Punkten minimieren. Diese Methode wird auch Chi-Quadrat-Minimierung genannt und wird wie folgt definiert:
wobei 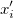 der Zeilenvektor für die i-te (i = 1, 2, …, n) Beobachtung ist. der Zeilenvektor für die i-te (i = 1, 2, …, n) Beobachtung ist.
Origin bietet zwei Optionen, um die Parameterwerte in der iterativen Prozedur anzupassen.
-
Algorithmus Levenberg-Marquardt (L-M)
Der Algorithmus Levenberg-Marquardt (L-M)11 ist eine iterative Prozedur, die die Gauss-Newton-Methode und die Methode des steilsten Abstiegs kombiniert. Der Algorithmus funktioniert gut für die meisten Fälle und ist Standard für nichtlineare Routinen der kleinste Quadrate.
- Berechnen Sie den
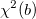 -Wert aus den gegebenen Initialisierungswerten: -Wert aus den gegebenen Initialisierungswerten: 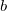 . .
- Wählen Sie einen moderaten Wert für
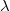 , sagen wir , sagen wir 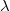 = 0,001. = 0,001.
- Löschen Sie die Levenberg-Marquardt-Funktion11 für
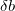 und werten Sie und werten Sie 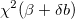 aus. aus.
- Wenn
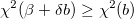 , erhöhen Sie , erhöhen Sie 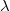 um einen Faktor von 10 und kehren Sie zurück zu Schritt 3. um einen Faktor von 10 und kehren Sie zurück zu Schritt 3.
- Wenn
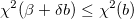 , verringern Sie , verringern Sie 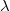 um einen Faktor von 10, aktualisieren Sie die Parameterwerte auf um einen Faktor von 10, aktualisieren Sie die Parameterwerte auf 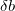 und kehren Sie zurück zu Schritt 3. und kehren Sie zurück zu Schritt 3.
- Stoppen Sie, bis die
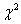 -Werte, die in zwei aufeinanderfolgenden Iterationen berechnet werden, klein genug sind (verglichen mit der Toleranz). -Werte, die in zwei aufeinanderfolgenden Iterationen berechnet werden, klein genug sind (verglichen mit der Toleranz).
Downhill-Simplex-Algorithmus
Neben der L-M-Methode bietet Origin auch eine Downhill-Simplex-Approximation9,10. In der Geometrie ist ein Simplex ein Polytop von N + 1 Sattelpunkten in N Dimensionen. Bei einer nichtlinearen Optimierung existiert ein Analogon für eine Zielfunktion von N Variablen. Während der Iterationen passt der Simplex-Algorithmus (auch bekannt als Nelder-Mead) den Parameter "Simplex" an, bis er bis zu einem lokalen Minimum konvergiert.
Anders als die L-M-Methode benötigt die Simplex-Methode keine Ableitungen und bleibt effektiv, auch wenn die Rechenbelastung gering ist. Normalerweise, wenn Sie keinen guten Wert für die Parameterinitialisierung erhalten haben, können Sie diese Methode ausprobieren, um den ungefähren Parameterwert zur weiteren Anpassungsberechnung mit L-M zu erhalten. Die Simplex-Methode ist insofern stabiler, als dass sie weniger in unbedeutendere Bereiche des Parameterraums wandert; allerdings ist sie im Allgemeinen langsamer als L-M, besonders in der Nähe eines lokalen Minimums. Tatsächlich gibt es keinen "perfekten" Algorithmus für eine nichtlineare Anpassung, und vieles kann das Ergebnis beeinflussen (z.b. Initialisierungswerte). Bei komplizierten Modellen ist eine Methode vielleicht besser geeignet als eine andere. Außerdem möchten Sie vielleicht beide Methoden testen, um die Anpassungsoperation durchzuführen.
Algorithmus der orthogonalen Distanzregression (ODR)
Der Algorithmus der ODR (Orthogonale Distanzregression) minimiert die Summe der Fehlerquadrate, indem sowohl Anpassungsparameter und Werte der unabhängigen Variable in dem iterativen Prozess angepasst werden. Das Residuum in der ODR ist nicht die Differenz zwischen dem beobachteten Wert und dem vorhergesagten Wert für die abhängige Variable, sondern die orthogonale Distanz zwischen den Daten zu der angepassten Kurve.
Origin verwendet den ODR-Algorithmus in ODRPACK958.
Für eine explizite Funktion könnte der ODR-Algorithmus folgendermaßen ausgedrückt werden:
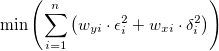
unterliegt den Nebenbedingungen:
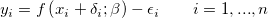
wobei 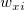 und und 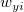 die Gewichtungen der Anwendereingabe von die Gewichtungen der Anwendereingabe von 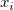 und und 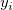 sind sowie sind sowie 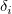 und und 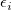 das Residuum der entsprechenden das Residuum der entsprechenden 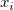 und und 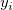 . . 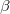 ist der Anpassungsparameter. ist der Anpassungsparameter.
Weitere Einzelheiten zum ODR-Algorithmus finden Sie unter ODRPACK958.
Vergleich zwischen ODR und L-M
Um zwischen ODR- und L-M-Algorithmus für Ihre Anpassung zu wählen, können Sie in der folgenden Informationstabelle nachlesen:
|
Orthogonale Distanzregression |
Levenberg-Marquardt |
| Anwendung |
Implizite und explicit Funktionen |
Nur explizite Funktionen |
| Gewichtung |
Unterstützt sowohl X- als auch Y-Gewichtung |
Unterstützt nur Y-Gewichtung |
| Residuumsquelle |
Die orthogonale Distanz von den Daten zu der angepassten Kurve |
Die Differenz zwischen dem beobachteten Wert und dem vorhergesagten Wert |
| Iterationsprozess |
Anpassen der Werte der Anpassungsparameter und der unabhängigen Variablen |
Anpassen der Werte der Anpassungsparameter |
Implizite Funktionen
Anpassungsmodell
Eine allgemeine implizite Funktion könnte ausgedrückt werden mit:
wobei 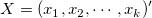 und und 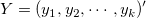 Variablen sind, Variablen sind, 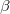 die Anpassungsparameter sind und die Anpassungsparameter sind und 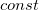 eine Konstante ist. eine Konstante ist.
 |
Beispiele für die implizite Funktion:
|
Algorithmus der orthogonalen Distanzregression (ODR)
Die ODR-Methode kann für sowohl implizite als auch explizite Funktionen verwendet werden. Um weitere Einzelheiten der ODR-Methode zu erfahren, lesen Sie bitte die Beschreibung der ODR-Methode im obigen Abschnitt.
Für implizite Funktionen könnte der ODR-Algorithmus folgendermaßen ausgedrückt werden:
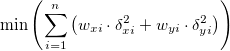
unter der Bedingung:
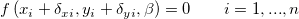
wobei 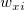 und und 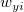 die Gewichtungen der Anwendereingabe von die Gewichtungen der Anwendereingabe von 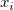 und und 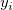 sind sowie sind sowie 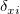 und und 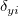 das Residuum der entsprechenden das Residuum der entsprechenden 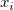 und und 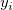 . . 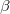 ist der Anpassungsparameter. ist der Anpassungsparameter.
Gewichtete Anpassung
Sind die Messfehler unbekannt, wird 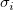 für alle i auf 1 gesetzt und die Anpassung ohne Gewichtung ausgeführt. Sind die Fehler aber bekannt, können wir diese Fehler als Gewichtungen betrachten und gewichtete Anpassung verwenden. In diesem Fall kann Chi^2 wie folgt dargestellt werden: für alle i auf 1 gesetzt und die Anpassung ohne Gewichtung ausgeführt. Sind die Fehler aber bekannt, können wir diese Fehler als Gewichtungen betrachten und gewichtete Anpassung verwenden. In diesem Fall kann Chi^2 wie folgt dargestellt werden:
Es sind eine Reihe von gewichteten Methoden in Origin verfügbar. Bitte entnehmen Sie weitere Informationen dem Abschnitt Anpassen mit Fehlern und Gewichtung in der Origin-Hilfe.
Parameter
Die mit der Anpassung verbundenen Formeln werden hier zusammengefasst:

Der angepasste Wert
Das Berechnen der angepassten Werte in nichtlinearer Regression ist eine iterative Vorgehensweise. Sie können eine kurze Einführung in dem oben stehenden Abschnitt lesen (So passt Origin die Kurve an) oder sich mit Hilfe des unten erwähnten Materials weiterführend informieren.
Die Parameterstandardfehler
Während der L-M-Iteration müssen wir die partielle Ableitungsmatrix F berechnen, deren Element in der i-ten Zeile und der j-ten Spalte folgendermaßen lautet:
wobei 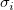 der Fehler von Y für die i-te Beobachtung ist, falls das instrumentelle Gewicht verwendet wird. Falls es kein Gewicht gibt, der Fehler von Y für die i-te Beobachtung ist, falls das instrumentelle Gewicht verwendet wird. Falls es kein Gewicht gibt, 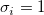 . Und . Und 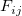 wird für jede Beobachtung wird für jede Beobachtung 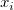 in jeder Iteration ausgewertet. in jeder Iteration ausgewertet.
Anschließend können wir die Varianz-Kovarianz-Matrix für die Parameter 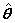 wie folgt ermitteln: wie folgt ermitteln:
wobei 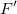 die Transponierte der F-Matrix ist. s2 ist die mittlere Residuenvarianz, auch als Reduziertes Chi-Quadrat bezeichnet oder die Abweichung des Modells, und kann folgendermaßen berechnet werden: die Transponierte der F-Matrix ist. s2 ist die mittlere Residuenvarianz, auch als Reduziertes Chi-Quadrat bezeichnet oder die Abweichung des Modells, und kann folgendermaßen berechnet werden:
wobei n die Anzahl der Punkte ist und p die Anzahl der Parameter.
Die Quadratwurzel des diagonalen Hauptwerts dieser Matrix C ist der Standardfehler des entsprechenden Parameters.
wobei Cii das Element in der i-ten Zeile und i-ten Spalte der Matrix C ist. Cij ist die Kovarianz zwischen θi und θj.
Sie können wählen, ob s2 ausgeschlossen wird, wenn die Kovarianzmatrix berechnet wird. Die hat Einfluss auf die Standardfehlerwerte. Beim Ausschließen von s2 deaktivieren Sie das Kontrollkästchen Reduziertes Chi^2 verwenden auf der Seite Erweitert im Bedienfeld Fit-Steuerung. Die Kovarianz wird dann berechnet durch:
Die Standardfehler sind dann:
Die Parameterstandardfehler kann uns einen Eindruck von der Genauigkeit der angepassten Werte geben. Normalerweise sollte der Betrag der Standardfehlerwerte niedriger sein als die angepassten Werte. Wenn die Standardfehlerwerte größer sind als die angepassten Werte kann das Anpassungsmodell überparameterisiert sein.
Der Standardfehler für abgeleitete Parameter
Origin schätzt die Standardfehler für die abgeleiteten Parameter gemäß der Fehlerverbreitungsformel, eine approximative Formel.
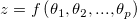 sei die Funktion mit einer Kombination von (linearen oder nichtlinearen) sei die Funktion mit einer Kombination von (linearen oder nichtlinearen) 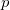 Variablen Variablen 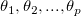 . .
Die allgemeine Regel der Fehlerverbreitung ist:
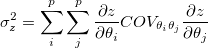
wobei 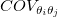 der Kovarianzwert für der Kovarianzwert für 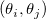 und und 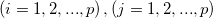 ist. ist.
Sie können wählen, ob die mittlere Residuenvarianz 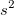 ausgeschlossen werden soll, wenn die Kovarianzmatrix ausgeschlossen werden soll, wenn die Kovarianzmatrix 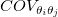 berechnet wird. Dies beeinflusst die Werte des Standardfehlers für abgeleitete Parameter. Beim Ausschließen von berechnet wird. Dies beeinflusst die Werte des Standardfehlers für abgeleitete Parameter. Beim Ausschließen von 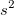 deaktivieren Sie das Kontrollkästchen Reduziertes Chi^2 verwenden auf der Seite Erweitert im Bedienfeld Fit-Steuerung. deaktivieren Sie das Kontrollkästchen Reduziertes Chi^2 verwenden auf der Seite Erweitert im Bedienfeld Fit-Steuerung.
Verwenden wir zum Beispiel drei Variablen:
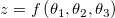
Dann haben wir:
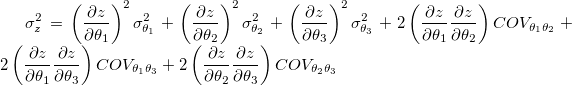
Jetzt sei der abgeleitete Parameter  und die Anpassungsparameter seien und die Anpassungsparameter seien 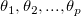 . Der Standardfehler für den abgeleiteten Parameter . Der Standardfehler für den abgeleiteten Parameter  ist ist 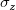 . .
Konfidenzintervalle
Origin bietet zwei Methoden zum Berechnen der Konfidenzintervalle für Parameter: Asymptotisch-Symmetrisch und Modellvergleich.
Asymptotisch-symmetrische Methode
Eine Annahme in der Regressionsanalyse ist, dass die Daten normalverteilt sind, so dass wir die Standardfehlerwerte verwenden können, um die Parameterkonfidenzintervalle zu erzeugen. Bei einem gegebenen Signifikanzniveau α ist das (1-α)x100%-Konfidenzintervall für den Parameter:
Das Parameterkonfidenzintervall gibt an, wie wahrscheinlich das Intervall den wahren Wert enthält.
Das oben dargestellte Konfidenzintervall ist Asymptotisch, die am häufigsten verwendete Methode zum Berechnen von Konfidenzintervallen. Das "Asymptotisch" meint hier, dass es sich um einen approximativen Wert handelt.
Methode des Modellvergleichs
Wenn Sie genauere Werte brauchen, können Sie die Methode des Modellvergleichs verwenden, um das Konfidenzintervall zu schätzen.
Wird die Methode Modellvergleich verwendet, werden die oberen und unteren Konfidenzgrenzen berechnet, indem die Werte für jeden Parameter p gesucht werden, bei dem RSS(j) (das über die verbleibenden Parameter minimiert wird) größer ist als RSS mit einem Faktor von (1+F/(n-p)).
wobei F = Ftable(α, 1, n-p) und RSS die minimale Fehlersumme der Quadrate ist, die während der Anpassungssitzung gefunden wurde.
t-Wert
Sie können entscheiden, einen t-Test für jeden Parameter auszuführen, um zu testen, ob sein Wert gleich Null ist. Die Nullhypothese des t-Tests für den j-ten Parameter ist:
Die Alternativhypothese ist:
Der t-Wert kann wie folgt berechnet werden:
Wahrsch.>|t|
Die Wahrscheinlichkeit, dass H0 in dem t-Test oben wahr ist.
wobei tcdf(t, df) die untere Wahrscheinlichkeit für die studentisierte t-Verteilung mit dem df-Freiheitsgrad berechnet.
Abhängigkeit
Ist eine Gleichung überparametrisiert, bestehen zwischen den Parametern wechselseitige Abhängigkeiten. Die Abhängigkeit des i-ten Parameters wird definiert als:
und (C-1)ii ist das (i, i)-te diagonale Element der Inversen der Matrix C. Liegt dieser Wert nahe bei 1, besteht eine starke Abhängigkeit.
Um weitere Informationen zu erhalten, wie die Werte die Qualität eines Anpassungsmodells bewerten, siehe die Seite Modelldiagnose mit Abhängigkeitswerten.
KI halbe Breite
Das Konfidenzintervall halbe Breite ist:
wobei OEG und UEG das obere Konfidenzintervall bzw. untere Konfidenzintervall ist.
Statistiken
Mehrere Statistikformeln für Anpassungen werden unten zusammengefasst:
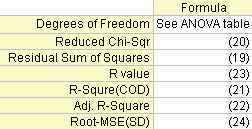
Freiheitsgrade
Der Freiheitsgrad Fehler Weitere Einzelheiten finden Sie in der ANOVA-Tabelle.
Summe der Fehlerquadrate
Residuensumme der Quadrate
Reduziertes Chi-Quadrat
Der Wert des reduzierten Chi-Quadrats, der gleich der Residuensumme des Quadrats geteilt durch den Freiheitsgrad ist
R-Quadrat (COD)
Der R2-Wert zeigt die Güte eines Fits und kann berechnet werden durch:
wobei TSS die Gesamtsumme der Quadrate und RSS die Residuensumme des Quadrats ist.
Kor. R-Quadrat
Der korrigierte R2-Wert:
R-Wert
Der R-Wert ist die Quadratwurzel von R2:
Weitere Informationen zu R2, korrigiertem R2 und R finden Sie im Abschnitt Güte des Fits.
Wurzel-MSE (StAbw)
Die Quadratwurzel des Mittelwerts des Fehlers oder die Standardabweichung der Residuen ist gleich der Quadratwurzel des reduzierten χ2:
ANOVA-Tabelle
Die ANOVA-Tabelle:
Hinweise: Die ANOVA-Tabelle ist für die Anpassung von impliziten Funktionen nicht verfügbar.
|
Freiheitsgrade |
Summe der Quadrate |
Mittelwert der Quadrate |
F -Wert |
Wahrsch. > F |
| Modell |
p
|
SSreg = TSS - RSS
|
MSreg = SSreg / p
|
MSreg / MSE
|
p-Wert
|
| Fehler |
n - p
|
RSS
|
MSE = RSS / (n-p)
|
|
|
| Unkorrigierte Gesamtsumme |
n
|
TSS
|
|
|
|
| Korrigierte Gesamtsumme |
n-1
|
TSS korrigiert
|
|
|
|
Hinweis: Bei der nichtlinearen Anpassung gibt Origin korrigierte und unkorrigierte Summen der Quadrate aus: Korrigiertes Modell:
Unkorrigiertes Modell:
Der F-Wert ist ein Test, ob das Anpassungsmodell sich signifikant von dem Modell Y = konstant unterscheidet. Zusätzlich werden der p-Wert bzw. die Signifikanzebene mit einem F-Test ermittelt. Wir können die Nullhypothese verwerfen, wenn der p-Wert kleiner als  ist, das heißt, das Anpassungsmodell unterscheidet sich signifikant von dem Modell Y = konstant. ist, das heißt, das Anpassungsmodell unterscheidet sich signifikant von dem Modell Y = konstant.
Konfidenz- und Prognosebänder
Konfidenzband
Das Konfidenzintervall für die Anpassungsfunktion besagt, wie gut Ihre Schätzung des Werts der Anpassungsfunktion bei bestimmten Werten der unabhängigen Variablen ist. Sie können mit einer Konfidenz von 100α% behaupten, dass der korrekte Wert für die Anpassungsfunktion sich innerhalb des Konfidenzintervalls befindet, in dem α das gewünschte Konfidenzniveau liegt. Dieses definierte Konfidenzintervall für die Anpassungsfunktion wird berechnet mit:
wobei:
Prognoseband
Das Prognoseband für das gewünschte Konfidenzniveau α ist das Intervall, in das erwartungsgemäß 100α% aller Versuchspunkte in einer Reihe wiederholter Messungen bei bestimmten Werten unabhängiger Variablen fallen. Dieses definierte Prognoseintervall für die Anpassungsfunktion wird berechnet als:
wobei
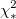 ist das reduzierte ist das reduzierte 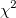
| Hinweise: Das Konfidenzband und das Prognoseband in dem angepassten Kurvendiagramm sind nicht für die Anpassung von impliziten Funktionen verfügbar. |
Weiterführende Themen
Referenz
- William. H. Press, etc. Numerical Recipes in C++. Cambridge University Press, 2002.
- Norman R. Draper, Harry Smith. Applied Regression Analysis, Third Edition. John Wiley & Sons, Inc. 1998.
- George Casella, et al. Applied Regression Analysis: A Research Tool, Second Edition. Springer-Verlag New York, Inc. 1998.
- G. A. F. Seber, C. J. Wild. Nonlinear Regression. John Wiley & Sons, Inc. 2003.
- David A. Ratkowsky. Handbook of Nonlinear Regression Models. Marcel Dekker, Inc. 1990.
- Douglas M. Bates, Donald G. Watts. Nonlinear Regression Analysis & Its Applications. John Wiley & Sons, Inc. 1988.
- Marko Ledvij. Curve Fitting Made Easy. The Industrial Physicist. Apr./May 2003. 9:24-27.
- "J. W. Zwolak, P.T. Boggs, and L.T. Watson, ``Algorithm 869: ODRPACK95: A weighted orthogonal distance regression code with bound constraints, ACM Transactions on Mathematical Software Vol. 33, Issue 4, August 2007."
- Nelder, J.A., and R. Mead. 1965. Computer Journal, vol. 7, S. 308 -313
- Numerical Recipes in C, Ch. 10.4, Downhill Simplex Method in Multidimensions.
- Numerical Recipes in C, Ch. 15.5, Nonlinear Models.
|