17.7.4.2 Interpreting Results of Discriminant AnalysisDiscAnalysis-Result
Discriminant Report Sheet
Descriptive Statistics
The descriptive statistics table is useful in determining the nature of variables. We will know magnitude and missing values of data. Inspection of means and SDs can reveal univariate/variance difference between the groups.
Covariance Matrix (Total)
The Covariance Matrix (Total) provide the covariance matrix of whole observations by treating all observations as from a single sample
Correlation Matrix (Total)
The table can be used to reveal the relationship between each variables.
Group Distance Matrix
The Group Distance Matrix provides the Mahalanobis distances between group means.
Univariate ANOVA
The table is to test the difference in group means for each variables. If the value of Prob>F is smaller than 0.05, it means the means of each group are significant different. Please note that if the variables are related, the result of table is not reliable . This univariate perspective does not account for any share variance(correlation) among the variables.
Equality Test of Covariance Matrices
Discriminant analysis assumes covariance matrices are equivalent. If the assumption is not satisfied, there are several options to consider, including elimination of outliers, data transformation, and use of the separate covariance matrices instead of the pool one normally used in discriminant analysis, i.e. Quadratic method
LOG of Determinants
The table output the natural log of the determinants of each group's covariance matrix and the pooled within-group covariance. Ideally the determinants should be almost equal to one another for the assumption of equality of covariance matrices.
Likelihood-ratio Test
The Likelihood-ratio test is to test whether the population covariance matrices within groups are equal. If the p-value > 0.05, we can say the covariance matrices are equal. Please note that the data is assumed to follow a multivariate Normal distribution with the variance-covariance matrix of the group. However, because discriminant analysis is rather robust against violation of these assumptions, as a rule of thumb we generally don't get too concerned with significant results for this test.
Pooled Within-group Covariance/Correlation Matrix
The Pooled Within-group Correlation matrix provides bivariate correlations between all variables. It can be used to detect potential problems with multicolliearity, Please pay attention if several correlation coefficient are larger than 0.8.
Within-group Covariance Matrix
Separate covariance matrices for each group.
Canonical Discriminant Analysis
Eigenvalues
The Eigenvalues table outputs the eigenvalues of the discriminant functions, it also reveal the canonical correlation for the discriminant function. The larger the eigenvalue is, the more amount of variance shared the linear combination of variables. The eigenvalues are sorted in descending order of importance. So the first one always explains that majority of variance in the relationship.
The second columns of the table, Percentage of Variance reveal the importance of the discriminant function. and the third column, Cumulative provides the cumulative percetage of the varaiance as each function is added the to table. If there are several discriminant functions, we can say the first few with comulative percetages largher than 90% are most important in the analysis.
The fourth column, Canonical Correlation provides the canonical correlation coefficient for each function. We can say the canonical correlation value is the r value between discriminat scores on the function and each group. It also can be used to compare the importance of each discriminant function.
Wilks' Lamba Test
Wilks' Lambda test is to test which variable contribute significance in discriminat function. The closer Wilks' lambda is to 0, the more the variable contributes to the discriminant function. The table also provide a Chi-Square statsitic to test the significance of Wilk's Lambda. If the p-value if less than 0.05, we can conclude that the corresponding function explain the group membership well.
Standardized Canonical Coefficients
The standardized canonical discriminant coefficients can be used to rank the importance of each variables. A high standardized discriminant function coefficient might mean that the groups differ a lot on that variable
Unstandardized Canonical Coefficients
The unstandardized canonical coefficients is the estimate of parameters, 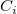 of the equation below of the equation below
where
-
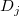 is the discriminant score for is the discriminant score for 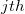 observation. observation.
-
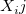 is the is the 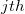 observation for the observation for the 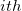 variable variable
The purpose of canonical discriminant analysis is to find out the best coefficient estimation to maximize the difference in mean discriminant score between groups.
Canonical Structure Matix
The canonical structure matrix reveals the correlations between each variables in the model and the discriminant functions. We can say they are factor loadings of the variables on each discriminant function. It allows us to compare correlations and see how closely a variable is related to each function. Generally, any variables with a correlation of 0.3 or more is considered to be important.
The canonical structure matrix should be used to assign meaningful labels to the discriminant functions. The standardized discriminant function coefficients should be used to assess the importance of each independent variable's unique contribution to the discriminant function.
Canonical Group Means
The Canonical group means is also called group centroids, are the mean for each group's canonical observation scores which are computed by equation (1). The larger the difference between the canonical group means, the better the predictive power of the canonical discriminant function in classifying observations.
Coefficients of Linear Discriminant Function
The Coefficients of Linear Discriminant Function table interprets the Fisher's theory, so is only available when Linear mode is selected for Discriminant Function
The linear discriminant functions, also called "classification functions" ,for each observation, have following form
where
-
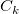 is the classification score for group is the classification score for group 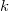
-
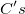 are the coefficients in table are the coefficients in table
For one observation, we can compute it's score for each group by the coefficients according to equation (2). The observation should be assign to the group with highest score.
In addition, the coefficients are helpful in deciding which variable affects more in classification. Comparing the values between groups, the higher coefficient means the variable attributes more for that group.
Classification Summary for Training Data
Classification Count
The rows in the Classification Count table are the observed groups of the observations and the columns are the predicted groups. Values in the diagonal of the table reflect the correct classification of observations into groups.
Error Rate
The Error Rate table lists the prior probability of each groups and the rate for misclassification.
Cross-validation Summary for Training Data
In cross-validation, each training data is treated as the test data, exclude it from training data to judge which group it should be classified to, and then verify whether the classification is correct or not. The Classification Count and the Error Rate table has the same meaning as Classification Summary for Training Data branch
Classification Summary for Test Data
The Classification Summary for Test Data table summarizes how to test data are classified. List how many test data in each groups and it's corresponding percent.
Classification Summary Plot
The Classification Summary Plot virtually shows the observed group v.s. predicted groups. The more the grouped color for the bar, the correcter the classification is.
Classification Fit Plot
Values in the diagonal of the classification table reflect the correct classification of individuals into groups by plotting the observation's posterior probability v.s their their scores on the discriminant dimensions. We should pay attention to the outliers in the plot, it shows the observation that might be misclassified to.
Canonical Score Plot
The canonical score plot shows how the first two canonical function classify observation between groups by plotting the observation score, computed via Equation (1). The plot provides a succinct summary of the separation of the observations. The clearer the observations are grouping to, the better the discriminant model is.
| Note: We only provides canonical score plot for the first two canonical functions, as they are also the two reflects the most variance in discriminant model. However, if you want to plot canonical score plot for other canonical functions, Please plot it by yourself with the data in Canonical Scores sheet
|
Training/Test Result
Classification
We will show the source training data, observed group and predicted group in the Training Results. From the From Group column and Allocated to Group column, we can conclude the Classification Summary for Training Data
Post Probabilities
The Post Probabilities indicates the probability that the observation in the group. The observation will be located to a group with the highest posterior probability.
Atypicality Index
The atypicality index presents the probabilities of obtaining an observation more typical of predicted group than the observed group. If most value in the atypicality index column are close to 1, it means the observations may come from a grouping not represented in the training set.
Distance
Distance is the Mahalanobis distrances from each of group means to the observation. The observation is classified to the group to which it is closest, i.e. the distance value is the smallest
Canonical Scores
The Canonical Scores sheet list the observations in training and test data set and their corresponding canonical scores computed by Equation (1)
|