17.4.1 One, Two, and Three Way ANOVAANOVA-CRD
Introduction
The factorial ANOVA models consider a completely randomized design for an experiment.
Origin supports following factorial ANOVA models
.
| Designs
|
Details
|
| One-way
|
compares three or more levels within one factor.
|
| Two-way
|
compare the effect of multiple levels of two factors, used to analyze the main effects of and interactions between two factors.
|
| Three-way (Pro Only)
|
tests for interaction effects between three independent variables on a continuous dependent variable (i.e., if a three-way interaction exists)
|
In addition to the analysis of variance, Origin also supports various methods for means comparison and actual and hypothetical power analysis.
Assumptions
The ANOVA model has the following assumptions:
- Independence
- The sample cases should be independent of each other. Otherwise you will need to use other ANOVA model, such as the repeated measure ANOVA
- Normality
- Data values of each combination of the groups should be from a normal distribution. We can use a normality test to verify this. However, please note that normal assumptions are usually not "fatal". Even you do not pass the normality test, you may still continue the ANOVA analysis if you have a large sample size.
- Homogeneity
- The variance between the groups should be equal. You can use the Homogeneity Tests(Levene's Test) to verify it. If the assumption is not satisfied, there are several options to consider, including elimination of outliers or data transformation. However, ANOVA is robust to the violation of this assumption. You may continue the study if the group size is equal.
Processing Procedure
Preparing Analysis Data
- Continuous Data
- Data of the dependent variable should be continuous.
- Independent random sample (no outliers)
- The sample cases should be independent of one another, i.e., no repeated measures or matched pairs data. In addition, the ANOVA model is sensitive to the inclusion of outliers. To observe the outliers, we can use Box plots or Outlier tests (Grubb's Test and Dixons Q-Test) to find the outliers and exclude them from the data
Verifying Assumptions
The normality test and the Homogeneity Tests(Levene's Test) can be used to verify the assumptions. Please see Assumptions for more information.
Selecting Mean Comparison Methods
Multiple comparison procedures are commonly used in an ANOVA after obtaining a significant omnibus test result. The significant ANOVA result suggests that the global null hypothesis, H0, is rejected. The H0 hypothesis states that the means are the same across the groups being compared. We can use multiple comparison to determine which means are different.
Origin provides eight different methods for means comparison. They are Tukey, Bonferroni, Dunn-Sidak, Fisher LSD, Scheffe, Holm-Bonferroni, and
Holm-Sidak.
| Tukey
|
The Tukey method controls the overall Type I error. When Tukey is used, the overall confidence level is 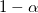 with equal sample sizes, that is, the risk of a Type I error is exactly with equal sample sizes, that is, the risk of a Type I error is exactly  ; while for unequal sample sizes, the risk of a Type I error is less than ; while for unequal sample sizes, the risk of a Type I error is less than 
|
| Bonferroni
|
The Bonferroni method controls the overall Type I error and is more conservative than Tukey. The method is commonly used for all pairwise comparisons tests.
|
| Fisher's LSD
|
Fishers LSD test dose not control the overall Type I error. Therefore, it should only be used for the significant overall F-test and the small number of comparisons.
|
| Scheffé
|
When the number of comparisons is small, Scheffé is very conservative (and more than Bonferroni). Scheffé is more powerful in cases of complex multiple comparisons, so it is used for complex multiple comparisons.
|
| Dunn-Sidak
|
This is a more powerful method than the Dunnett test method, especially when the number of comparisons is large.
|
| Holm-Bonferroni
|
This method is less conservative and more powerful than the Bonferroni method. Hence you have more chances to reject null hypotheses with the Bonferroni-Holm method.
|
| Holm-Sidak
|
The method is more powerful than Holm test. However, it can not be used to compute a set of confidence intervals.
|
Power Analysis
The power analysis procedure calculates the actual power for the sample data, which let you know the % chance of detecting a difference. It also helps you to calculate the hypothetical power if additional sample sizes are specified
Handling Missing Values
The missing values in the data range will be excluded in the analysis
From Origin 2015, missing values in the grouping range and the corresponding data values will be excluded in analysis. In the previous version, missing values in the grouping range will be considered as a group.
Performing ANOVA
| Features
|
Menu Entry
|
| One-way
|
Statistics: ANOVA: One-Way ANOVA
|
| Two-way
|
Statistics: ANOVA: Two-Way ANOVA
|
| Three-way (Pro Only)
|
Statistics: ANOVA: Three-Way ANOVA
|
|
Topics covered in this section:
- Three-Way ANOVA (Pro Only)
|
|