2.4.3 fitcmpmodel(Pro)
Menu Information
Compare Models
Brief Information
Compare two fitting models for a given dataset
Additional Information
It is not accessible from script. This feature is for OriginPro only.
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Fit Result1
|
result1
|
Input
Range
|
|
Specifies fit report sheets fitting with same datasets and different model.
|
| Fit Result2
|
result2
|
Input
Range
|
|
Specifies fit report sheets fitting with same datasets and different model.
|
| Akaike's Information Criteria (AIC)
|
aic
|
Input
int
|
1
|
Decide whether to output result of Akaike's Information Creiteria (AIC) for comparison. The method has less limitation for model comparison.
|
| Bayesian Information Criteria (BIC)
|
bic
|
Input
int
|
0
|
Select to decide whether to output result of Bayesian Information Criteria (BIC) for comparison. BIC introduces a larger penalty term than AIC to resolve overfitting problem in data fitting.
|
| F-test
|
ftest
|
Input
int
|
0
|
Decide whether to output result of F-test for comparison. Please note that F-test only makes sense for nested models.
|
| Significance Level
|
sl
|
Input
double
|
0.05
|
Values between 0 and 1 are supported.
|
| Fit Parameters
|
param
|
Input
int
|
1
|
Decide whether to output Fit Parameter table for comparison.
|
| Fit Statistics
|
statics
|
Input
int
|
1
|
Decide whether to output Fit Statistics table for comparison.
|
| 1st Model Name
|
name1
|
Input
string
|
Model1
|
Specify the display name for the first model in the report sheet.
|
| 2nd Model Name
|
name2
|
Input
string
|
Model2
|
Specify the display name for the second model in the report sheet.
|
| Results
|
rt
|
Output
ReportTree
|
<new>
|
Specify where to put the output report.
|
Description
This tool helps to find out which model is the best fit for the same dataset.
Usually we have learned to compare values of Reduced Chi-Square to select the best fit model. It is a useful measure of goodness-of-fit. The more it is close to 1.0, the better model describes our data. But, since variance of each point which enters in the calculation of Chi-Square is not sufficiently known, Chi-Square criteria is not significant in a statistical sense.
So, we adopt the following 2 methods in model comparison.
F-test
F-test takes advantage of difference of the sum square of residuals of each fit to find out which model is the best. F-test is to compare the sum of square of residuals into a component removed by the simpler model and into a component additionally removed by the more complex model. So, it only makes sense when two models are nested. We recommend users to use this method in following situation
1. Equation of 2 models should be in similar structure , such as:
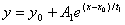 vs. vs. 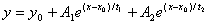
2. Model with some parameter fixed vs. Model with no parameter fixed
Akaike's Information Criteria (AIC)
Akaike's Information Criteria is to find which model would best approximate reality given the data we have recorded. It can simultaneously compare nested or non-nested models. Not relying on concept of significance, AIC is founded on maximum likelihood to rank models. So robust and precise estimates can be obtained by incorporating model uncertainty based on AIC.
To use this tool, please pay attention to following
- Input for this tool is fit report sheets (Linear Fit, Polynomial, Nonlinear Curve Fit, etc). So fit tools need to be run before you use this tool
- Only the 1st result in report sheet can be found. So we need to ensure that results are in separate sheet when fitting multiple datasets.
Bayesian Information Criteria (BIC)
Bayesian information criterion is a model selection criterion that was derived by Schwarz (1978) from a Bayesian modification of the AIC criterion. The penalty term for BIC is similar to AIC equation, but uses a multiplier of ln(n) for k instead of a constant 2 by incorporating the sample size n. That can resolve so called over fitting problem in data fitting.
For two models compared, the model with lower value of BIC is preferred by data.
Examples
This example compares the two models as described below.
fname$=system.path.program$ + "Samples\Curve Fitting\Exponential Decay.dat"; // prepare the data
newbook;
impasc;
nlbegin 1!2 ExpDec1 tt; // nonlinear fitting on column 2
nlfit;
nlend 1 2; ;
nlbegin 1!2 ExpDec2 tt; // nonlinear fitting on column 3
nlfit;
nlend 1 2;
fitcmpmodel -r 2 result1:=2! result2:=4!; // compare the two models
Suppose we have a dataset and want to see which model is the best fit model for it.
Candidate models are:
ExpDec1: 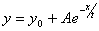
ExpDec2: 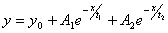
Operation
1.Import Exponential Growth.dat on \Samples\Curve Fitting folder
2.Highlight Col(B), select Analysis: Fitting: Nonlinear Curve Fit to open dialog. Set Function as ExpDec1. Click OK to get result sheet
3.Open Nonlinear Curve fit dialog again, Set Function as ExpDec2 this time. Click OK to get result sheet
4.Select Analysis: Fitting: Compare Models to open dialog
5.Click browse button to open Report Tree Browser and select 1 item for Fit Result1
6.Repeat same operation to select another item for Fit Result2
7. Select all options in GUI and click OK
8.From F-test table and AIC result table, we can draw conclusion that ExpDec1 function is the best fit model
Algorithm
1. F-test
F Statistic:
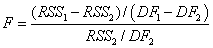
- RSS1 is residual sum of square of fit for the simpler model, RSS2 is residual sum of square of fit for the other model.
Prob:
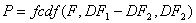
2. Akaike's Information Criteria (AIC)
AIC:
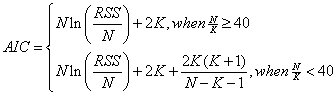
- where N is number is data points, K is number of parameters plus 1, RSS is residual sum of square of fit.
Weight:
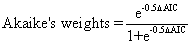
- where
 is the deference between two AIC values is the deference between two AIC values
3. Schwarz Bayesian Information Criterion (BIC)
BIC:
-
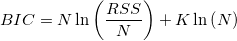
- where N is number is data points, K is number of parameters plus 1, RSS is residual sum of square of fit.
References
1. Akaike, Hirotsugu (1974). "A new look at the statistical model identification". IEEE Transactions on Automatic Control19 (6): 716-723
2. Burnham, K. R. and D. R. Anderson. 2002. Model Selection and Multimodel Inference. Springer, New York.
Related X-Functions
fitcmpdata
|