11.2.6 Tutorial:Calling NAG Functions From Origin COC-Call-NAG
Summary
Calling a NAG function from an Origin C function is very much like calling any other Origin C function. You must familiarize yourself with the desired NAG function to gain an understanding of what parameters the function requires to be passed as arguments and what parameters the function returns. Once familiar with the function, you must develop code that follows the function's requirements.
The NAG header file containing the function's prototype must be included, required parameters must be correctly declared, sized, and initialized, and the function call must follow the function's prototype as described in header file. The objective of this tutorial is to demonstrate how to call a NAG function from an Origin C function.
Minimum Origin Version Required: Origin 8.1 SR1
What you will learn
This tutorial will show you how to:
- Understand NAG functions
- Get Ready to Debug Sample Code
- Include the NAG Header
- How to See the Declaration of NAG Function
- How to Get NAG Error Code
- How to Use Function Pointer
Understand NAG Functions
The primary resource for understanding NAG functions is NAG library. The library also can be found in Origin C Reference. For example, d01sjc NAG function:
- From the Origin menu select Help:Programming:OriginC. In the Origin C Reference book, expand the Global Functions book, expand the NAG Functions book, and choose Accessing NAG Functions Category and Help.
- Select Quadrature (d01) category and then select nag_1d_quad_gen_1 (d01sjc) function.
- The selected page is one PDF file. Study the nag_1d_quad_gen_1 function as needed to understand the description of the function, the function's prototype, and the description of all arguments. Sample data and an example program calling the function are also often included.
Secondary resource for understanding the Origin C NAG functions is Examples book. From the Origin menu select Help:Programming:OriginC, expand Examples book, expand Analysis book, choose Accessing NAG Functions, there are some examples to show how to call NAG functions in Origin C.
Get Ready to Debug Sample Code
The best way to understand how to write an Origin C function that calls a NAG function is to step through an example function in Debug mode. Follow the steps below to set up Origin and Code Builder to execute such a sample Origin C function in Debug mode.
- From the Code Builder menu, select File: New. This opens the New File dialog box.
- In the File Name text box, type: TestNAG, Keep Add to Workspace checkbox is checked. Click OK. The file TestNAG.c is added to the workspace.
- Select and copy the following function, and paste it into the TestNAG.c file. Be sure to paste the text below the line that reads "// Include your own header files here."
// Include your own header files here.
#include <OC_nag.h>
// Start your functions here.
//NAG_CALL denotes proper calling convention. You may treat it like a function pointer
//and define your own integrand
static double NAG_CALL f_callback_ex(double x, Nag_User *comm)
{
int *use_comm = (int *)comm->p;
return (x*sin(x*30.0)/sqrt(1.0-x*x/(PI*PI*4.0)));
}
void nag_d01sjc_ex()
{
double a = 0.0;
double b = PI * 2.0; // integration interval
double epsabs, abserr, epsrel, result;
// you may use epsabs and epsrel and this quantity to enhance your desired precision
// when not enough precision encountered
epsabs = 0.0;
epsrel = 0.0001;
// The max number of sub-intervals needed to evaluate the function in the integral
// The more diffcult the integrand the larger max_num_subint should be
// For most problems 200 to 500 is adequate and recommmended
int max_num_subint = 200;
Nag_QuadProgress qp;
NagError fail;
Nag_User comm;
static int use_comm[1] = {1};
comm.p = (Pointer)&use_comm;
//Note:nag_1d_quad_gen (d01ajc) has been replaced by nag_1d_quad_gen_1 (d01sjc) at Mark 25
d01sjc(f_callback_ex, a, b, epsabs, epsrel, max_num_subint,&result, &abserr, &qp, &comm, &fail);
// For the error other than the following three errors which are due to bad input parameters
// or allocation failure NE_INT_ARG_LT NE_BAD_PARAM NE_ALLOC_FAIL
// You will need to free the memory allocation before calling the integration routine again to
// avoid memory leakage
if (fail.code != NE_INT_ARG_LT && fail.code != NE_BAD_PARAM && fail.code != NE_ALLOC_FAIL)
{
NAG_FREE(qp.sub_int_beg_pts);
NAG_FREE(qp.sub_int_end_pts);
NAG_FREE(qp.sub_int_result);
NAG_FREE(qp.sub_int_error);
}
printf("%10.6f", result);
}
Include the NAG Header
#include <OC_nag.h>
This header file containing all the header files of NAG functions, and all type define and error code define. So just include this one function should be enough.
How to See the Declaration of NAG Function
See the declaration of NAG functions from the header file:
- Acivate TestNAG.c file that created in above section, move scoll bar to find out #include <OC_nag.h> line.
- Right click anywhere in the line and select Open "OC_nag.h". This opens the NAG header file.
- Move scoll bar to find out #include <NAG_MARK25\oc_nag_all.h> line, and also right click to select Open "NAG_MARK25\oc_nag_all.h". This opens the header file containing all nag headers at Mark25.
- In the Search combo box
 type nagd01.h and press ENTER button to find out this line. Function d01sjc belongs to d01 category, so the header file name should be nagd01.h. type nagd01.h and press ENTER button to find out this line. Function d01sjc belongs to d01 category, so the header file name should be nagd01.h.
- Right click anywhere of this line to choose Open "nagd01.h". This opens the header file including the prototype of the functions.
- In the Search combo box, type d01sjc and press ENTER button to go to the declaration of this function.
To see the declaration of functions from NAG PDF:
How to Get NAG Error Code
- Reactivate the TestNAG.c window in Code Builder. In this file, the NagError variable fail is defined and passed as last argument to function d01sjc.
- NAG function returns error code into NagError variable code item. In this example, can access NAG error code by fail.code.
How to know what error codes will be got:
- Open Origin C Help from Origin menu Help: Programming: OriginC, expand Origin C Reference book, Global Functions book, NAG Functions book and choose Accessing NAG Functions Category and Help.
- In Chapters of NAG C Library table, choose d01 to enter Quadrature page, select d01sjc in the table of this category to open the PDF help of this NAG function.
- Drag scall bar to page down to 6 Error Indicators and Warnings part, there list all error codes for this function and the related description. Can directly use these error codes in Origin C if included correct header file (include <OC_nag.h>, this header containing all NAG headers), for example NE_INT_ARG_LT, NE_BAD_PARAM, NE_ALLOC_FAIL used in TestNAG.c file.
How to Use Function Pointer
- Open nagd01.h file from Origin program path \OriginC\system\NAG_MARK25 folder.
- In this file, find out the declaration of d01sjc function. The first argument type of this function is NAG_D01SJC_FUN.
- Double-click NAG_D01SJC_FUN to high-light it. From menu choose Edit: Find in Files to open Find in Files dialog. Set settings same as the following picture, click Find button.
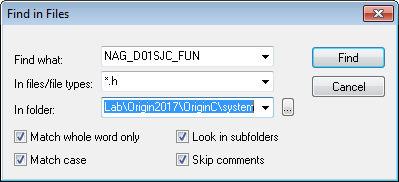
- Searching result display in Output window. Double click nag_types.h line to go to this file, typedef NAG_D01_TS_FUN NAG_D01SJC_FUN line, you can find the define of NAG_D01_TS_FUN nearby.
- The define of NAG_D01_TS_FUN is
typedef double (NAG_CALL * NAG_D01_TS_FUN)(double, Nag_User *comm); User defined function should keep the same return type and argument list as this define. And NAG_CALL denotes proper calling convention and it should be used in your own function.
- Activate TestNAG.c file. There is a function named f_callback_ex and it used as function pointer in d01sjc as the first argument.
double NAG_CALL f_callback_ex(double x, Nag_User *comm)
{
int *use_comm = (int *)comm->p;
return (x*sin(x*30.0)/sqrt(1.0-x*x/(PI*PI*4.0)));
}
|