4.2.2.27 Fitting with Convolution of Two FunctionsFitting-Convolution-2Funcs
Summary
In this tutorial, we will show you how to define a convolution of two functions, and perform a fit of the data with non-evenly spaced X using this fitting function.
 | If your data is a convolution of Gauss and Exponential functions, you can simply use built-in fitting function GaussMod in Peak Functions category to directly fit your data.
|
Minimum Origin Version Required: Origin 9.0 SR0
What you will learn
This tutorial will show you how to:
- Sample a function.
- Calculate a convolution of two functions.
- Define constants in the fitting function.
- Pad zeroes before the convolution.
- Interpolate the convolution result for non-evenly spaced X.
- Use a parameter to balance the speed and the precision.
- Use Y Error Bar as weight.
Example and Steps
Import Data
- Start with an empty workbook. Select Help: Open Folder: Sample Folder... to open the "Samples" folder. In this folder, open the Curve Fitting subfolder and find the file ConvData.dat. Drag-and-drop this file into the empty worksheet to import it. Note that column A is not evenly spaced. We can use LabTalk diff function to verify it.
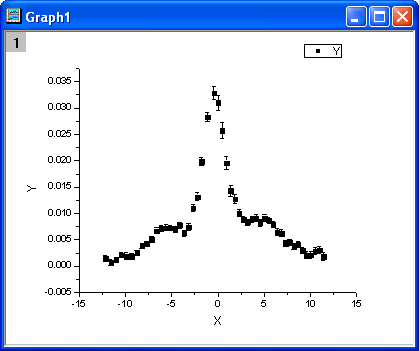
- Right click on column C, and select Set As: Y Error from the short-cut menu. Highlight column B and C, and select Plot: Symbol: Scatter from the Origin menu. The graph should look like:
Define Fitting Function
The fitting function is a convolution of two functions. It can be described as follows:
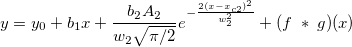
where 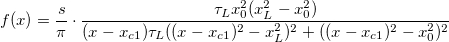 , ,
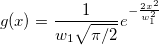 . .
And  , , 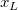 , , 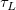 , s, , s, 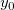 , , 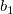 and and 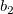 are fitting parameters. are fitting parameters. 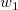 , ,  , , 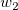 , , 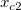 and and 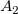 are constants in the fitting function. are constants in the fitting function.
The fitting function can be defined using the Fitting Function Builder tool.
- Select Tools: Fitting Function Builder from Origin menu.
- In the Fitting Function Builder dialog's Goal page, click Next.
- In the Name and Type page, select User Defined from Select or create a Category drop-down list, type convfunc in the Function Name field, and select Origin C in Function Type group. And click Next.
- In the Variables and Parameters page, type x0,xL,tL,s,y0,b1,b2 in the Parameters field, w1,xc1,w2,xc2,A2 in the Constants field. Click Next.
- In the Origin C Fitting Function page, set initial parameters as follows:
x0 = 3.1
xL = 6.3
tL = 0.4
s = 0.14
y0 = 1.95e-3
b1 = 2.28e-5
b2 = 0.2
Click Constants tab, set constants as follows:
w1 = 1.98005
xc1 = -0.30372
w2 = 5.76967
xc2 = 3.57111
A2 = 9.47765e-2
Click the  button on the right of the Function Body edit box and define the fitting function in Code Builder as follows: button on the right of the Function Body edit box and define the fitting function in Code Builder as follows:
Include header files,
#include <ONLSF.H>
#include <fft_utils.h>
Define the function body
NLFitContext *pCtxt = Project.GetNLFitContext();
if ( pCtxt )
{
// Vector for the output in each iteration.
static vector vX, vY;
static int nSize;
BOOL bIsNewParamValues = pCtxt->IsNewParamValues();
// If parameters were updated, we will recalculate the convolution result.
if ( bIsNewParamValues )
{
//Sampling Interval
double dx = 0.05;
vX.Data(-16.0, 16.0, dx);
nSize = vX.GetSize();
vector vF, vG, vTerm1, vTerm2, vDenominator, vBase, vAddBase;
double Numerator = tL * x0^2 * (xL^2 - x0^2);
vTerm1 = ( (vX - xc1) * tL * ( (vX - xc1)^2 - xL^2 ) )^2;
vTerm2 = ( (vX - xc1)^2 - x0^2 )^2;
vDenominator = vTerm1 + vTerm2;
//Function f(x)
vF = (s/pi) * Numerator / vDenominator;
//Function g(x)
vG = 1/(w1*sqrt(pi/2))*exp(-2*vX^2/w1^2);
//Pad zeroes at the end of f and g before convolution
vector vA(2*nSize-1), vB(2*nSize-1);
vA.SetSubVector( vF );
vB.SetSubVector( vG );
//Perform circular convolution
int iRet = fft_fft_convolution(2*nSize-1, vA, vB);
//Truncate the beginning and the end
vY.SetSize(nSize);
vA.GetSubVector( vY, floor(nSize/2), nSize + floor(nSize/2)-1 );
//Baseline
vBase = (b1*vX + y0);
vAddBase = b2 * A2/(w2*sqrt(pi/2))*exp( -2*(vX-xc2)^2/w2^2 );
//Fitted Y
vY = dx*vY + vBase + vAddBase;
}
//Interpolate y from x for the fitting data on the convolution result.
ocmath_interpolate( &x, &y, 1, vX, vY, nSize );
}
Click Compile button to compile the function body. And click the Return to Dialog button.
Click Evaluate button, and it shows y=0.02165 at x =1. And this indicates the defined fitting function is correct. Click Next.
- Click Next. In the Bounds and General Linear Constraints page, set the following bounds:
0 < x0 < 7
0 < xL < 10
0 < tL < 1
0 <= s <= 5
0 < b2 <= 3
Click Finish.
| Note: In order to monitor the the fitted parameters, NLFitContext class was introduced in defining fitting function to achieve some key information within the fitter
|
Fit the Curve
- Select Analysis: Fitting: Nonlinear Curve Fit from the Origin menu. In the NLFit dialog, select Settings: Function Selection, in the page select User Defined from the Category drop-down list and convfunc function from the Function drop-down list. Note that Y Error Bar is shown in the active graph, so column C is used as Y weight, and Instrumental weighting method is chosen by default.
- Click the Fit button to fit the curve.
Fitting Results
The fitted curve should look like:
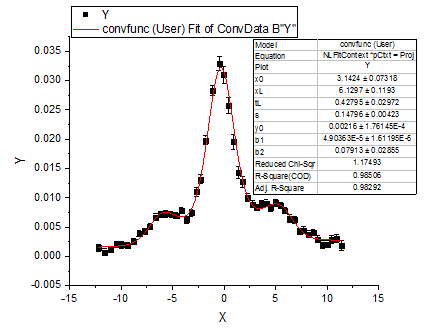
Fitted Parameters are shown as follows:
| Parameter
|
Value
|
Standard Error
|
| x0
|
3.1424
|
0.07318
|
| xL
|
6.1297
|
0.1193
|
| tL
|
0.42795
|
0.02972
|
| s
|
0.14796
|
0.00423
|
| y0
|
0.00216
|
1.76145E-4
|
| b1
|
4.90363E-5
|
1.61195E-5
|
| b2
|
0.07913
|
0.02855
|
Note that you can set a smaller value for dx in the fitting function body, the result may be more accurate, but at the same time it may take a longer time for fitting.
|