2.11.18 stft(Pro)
Menu Information
Analysis : Signal Processing : STFT
Brief Information
Compute short time fourier transform of signal
Additional Information
This feature is for OriginPro only.
Command Line Usage
1. stft ix:=col(2);
2. stft ix:=col(2) interval:=4;
3. stft ix:=col(2) option:=complex;
4. stft ix:=col(2) winlen:=32 fftlen:=64 overlap:=16;
5. stft ix:=col(2) win:=tri;
6. stft ix:=col(2) win:=gauss correct:=power alpha:=3;
7. stft ix:=col(2) win:=kaiser beta:=2;
8. stft ix:=col(2) plot:=0;
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
ix
|
Input
vector<complex>
|
<active>
|
Specifies the input signal
|
| Specify By
|
mode
|
Input
int
|
0
|
Option list:
- interval:Interval {0}
- freq:Frequency {1}
|
| Sampling Interval
|
interval
|
Input
double
|
<auto>
|
Specifies the sampling interval if mode is interval. The default is <auto>, which corresponds to an automatically-calculated interval.
|
| Sampling Frequency
|
freq
|
Input
double
|
<auto>
|
Specifies the sampling frequency if mode is frequency. The default is <auto>, which corresponds to an automatically-calculated frequency.
|
| FFT Length
|
fftlen
|
Input
int
|
256
|
Specifies the size of FFT section
|
| Window length
|
winlen
|
Input
int
|
256
|
Specifies the window size, which must not be greater than the size of an FFT section
|
| Overlap
|
overlap
|
Input
int
|
128
|
Specifies the number of data points by which the window sections overlap. It should be less than the window size
|
| Window Type
|
win
|
Input
int
|
4
|
Specifies the window type used by FFT
Option list:
- rect:Rectangle {0}
- Rectangular window
- welch:Welch {1}
- Welch window
- tri:Triangular {2}
- Triangular window
- bartlett:Bartlett {3}
- Bartlett window
- hanning:Hanning {4}
- Hanning window
- hamming:Hamming {5}
- Hamming window
- blackman:Blackman {6}
- Blackman window
- gauss:Gaussian {7}
- Gaussian window
- kaiser:Kaiser {8}
- Kaiser window
|
| Alpha
|
alpha
|
Input
double
|
0
|
This variable is only available when Window Type is Gaussian. It specifies the Alpha parameter for Gaussian window.
|
| Beta
|
beta
|
Input
double
|
0
|
This variable is only available when Window Type is Kaiser. It specifies the Beta parameter for Kaiser window.
|
| Window Correction
|
correct
|
Input
int
|
amplitude
|
Specifies the Window Correction Factor used to correct the alteration made by applying a window to the input data.
Option list
- none:None
- No correction is applied.
- amp:Amplitude
- Amplitude Correction is applied.
- power:Power
- Energy Correction is applied.
|
| Option
|
option
|
Input
int
|
2
|
Specifies the computation option. The default is 2, which correspond to the computing of the amplitude in dB.
Option list:
- complex:Complex Result {0}
- The complex result of STFT will be computed.
- amp:Amplitude Result {1}
- The amplitude of the complex result will be given
- ampdb:Amplitude in dB {2}
- The amplitude in dB will be computed.
|
| Swap Time and Frequency
|
swapxy
|
Input
int
|
0
|
Specifies whether to swap the time axis and the frequency axis in the image plot.
|
| Output Matrix
|
om
|
Output
MatrixObject
|
[<new>]<new>!
|
Specify the output matrix
|
| Create Image Plot
|
plot
|
Input
int
|
1
|
Specify whether an image plot of the result will be generated
|
| Output Worksheet
|
rd
|
Output
ReportData
|
[<input>]<new>
|
Specify the output worksheet.
|
Examples
1. To perform stft of Column B using the default setting:
stft ix:=col(b)
2. To perform stft with Hanning window:
stft -d
to open the dialog. Then select Hanning window for Window Type.
3. To perform stft using a pre-saved analysis theme called MyTheme, use the Command Window:
stft -t "MyTheme"
Algorithm
stft Computation
stft is computed in the following procedure:
1. N points are taken from the input signal, where N is equal to the window size.
2. A window of the chosen type is used to multiply the extracted data, point-by-point.
3. Zeros will be padded on both sides of the window, if the window size is less than the size of the FFT section.
4. FFT is computed on the FFT section.
5. Move the window according to the user-specified overlap size, and repeat steps 1 through 4 until the end of the input signal is reached.
The Window Functions
The sliding windows are defined as follows:
Rectangular Window:
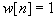 for for 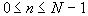
Welch Window:
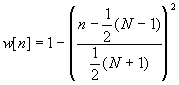 for for 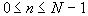
Triangular Window:
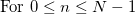
![w[n]=
\begin{cases}
\frac{2}{N+1}(\frac{N+1}{2}-|n-\frac{N-1}{2}|), & \mbox{if }N\mbox{ is odd} \\
\frac{2}{N}(\frac{N}{2}-|n-\frac{N-1}{2}|), & \mbox{if }N\mbox{ is even}
\end{cases}
w[n]=
\begin{cases}
\frac{2}{N+1}(\frac{N+1}{2}-|n-\frac{N-1}{2}|), & \mbox{if }N\mbox{ is odd} \\
\frac{2}{N}(\frac{N}{2}-|n-\frac{N-1}{2}|), & \mbox{if }N\mbox{ is even}
\end{cases}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/XFunction/images/Stft/math-1e13169a1ecddcba2b5478ade624ef7d.png?v=0)
Bartlett Window:
![w[n]=\frac{2}{N-1}(\frac{N-1}{2}-|n-\frac{N-1}{2}|) \mbox{ for } 0 \le n \le N-1 w[n]=\frac{2}{N-1}(\frac{N-1}{2}-|n-\frac{N-1}{2}|) \mbox{ for } 0 \le n \le N-1](//d2mvzyuse3lwjc.cloudfront.net/doc/en/XFunction/images/Stft/math-44e773c8628ca87ab69ebfe21712169d.png?v=0)
Hanning Window:
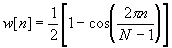 for for 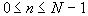
Hamming Window:
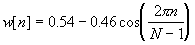 for for 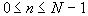
Blackman Window:
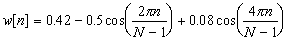 for for 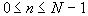
Gaussian Window:
![w[n]=e^{-\frac{1}{2}(\alpha\frac{n-(N-1)/2}{(N-1)/2})^2} \mbox{ for } 0 \le n \le N-1 w[n]=e^{-\frac{1}{2}(\alpha\frac{n-(N-1)/2}{(N-1)/2})^2} \mbox{ for } 0 \le n \le N-1](//d2mvzyuse3lwjc.cloudfront.net/doc/en/XFunction/images/Stft/math-8c1b29b5709e6b785032092404883df0.png?v=0)
Kaiser Window:
![w[n]=\frac{I(\beta\sqrt{1-(\frac{2n}{N-1}-1)^2})}{I(\beta)} \mbox{ for } 0 \le n \le N-1 w[n]=\frac{I(\beta\sqrt{1-(\frac{2n}{N-1}-1)^2})}{I(\beta)} \mbox{ for } 0 \le n \le N-1](//d2mvzyuse3lwjc.cloudfront.net/doc/en/XFunction/images/Stft/math-6ac7c1069e87a335854c91b9b9ff2e79.png?v=0)
where I(ix) denotes Bessel Function.
Computation of the Sampling Interval
For details of the auto computation of the sampling interval, please see the X-Function document for fft1.
More Information
For more information, please refer to our User Guide.
Related X-Functions
fft1
Keywords:fft, sliding window, time slice
|