2.13 Compare NLFit Parameters/Datasets

1 Examples
2 Dialog Settings
3 Algorithm
- 3.1 Akaike Information Criteria(AIC)
- 3.2 F-test

This app, Compare Datasets and Fit Parameters is used to compare NLFit parameters for multiple datasets, and determine whether they are different. This tool can also be used to compare datasets using a fitting function.

Examples

Import Dose Response - Inhibitor.dat in \\Samples\Curve Fitting folder to a new worksheet.
Right click on column A, select Set Column Values from the shortcut menu, in the opened dialog, type log(col(A)) in the box.
Highlight columns B, C and D, click Scatter button. The graph will look like as below.
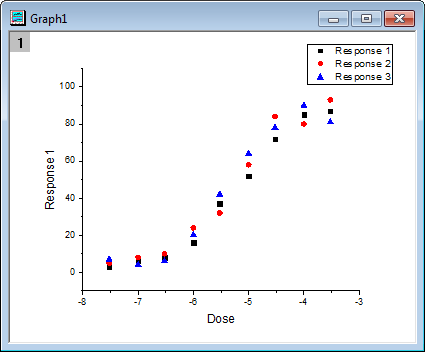
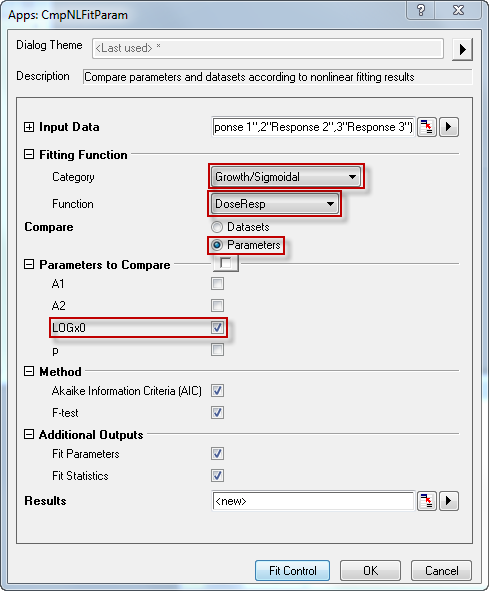
Click the Compare NLFit Parameters/Datasets button in Apps docked toolbar. In the opened dialog, choose Growth/Sigmoidal from Category drop-down list in Fitting Function branch, and select DoseResp from Function drop-down list. Choose Compare Parameters. Click Fit Control button, you can modify initial values and see the preview for fitting function at given initial values. In Parameters to Compare branch, select LOGx0. The dialog setting is shown as below:
Click OK button. The report should look like as below:

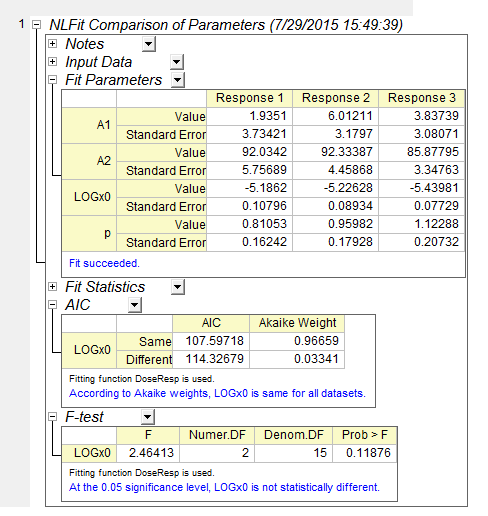
It can be seen that for this example, LOGx0 is same in both methods.

Dialog Settings

Input Data

Specify datasets for nonlinear curve fit comparison of parameters/datasets.

Fitting Function

Category	Specify the category for fitting functions. Function drop-down list will list all functions in the category.
Function	Specify the fitting function for nonlinear curve fit comparison.

Compare

Specify whether to compare Datasets or Parameters.

Datasets

Compare datasets and see whether they are same.

Parameters

Compare parameters and see whether specified parameters in the fitting functions for all datasets are same.

Parameters to Compare

Choose parameters in the fitting function to compare. Note that parameters fixed or shared are not listed here.

Method

Specify the comparison algorithm.

Akaike Information Criteria(AIC)	Comparison conclusion is made according to Akaike's weight.
F-test	Comparison conclusion is made according to P-value in F-test.

Additional Outputs

Specify whether to output fitting tables.

Fit Parameters	Decide whether to output Fit Parameters table for each dataset.
Fit Statistics	Decide whether to output Fit Statistics table for each dataset.

Results

Specify the output report worksheet for the comparison result.

Fit Control button

Click this button, it will open the Fit Control dialog, which allows you to control the fitting for datasets.

Fit Control Dialog

Parameters tab

The Parameters tab lists all the parameters of the chosen function for all datasets. The columns that are shown in the tab contain check boxes to control whether a parameter should be varied or fixed during the iterative fitting process. You can also use this tab to specify which parameters should be shared, and define initial values and bounds.

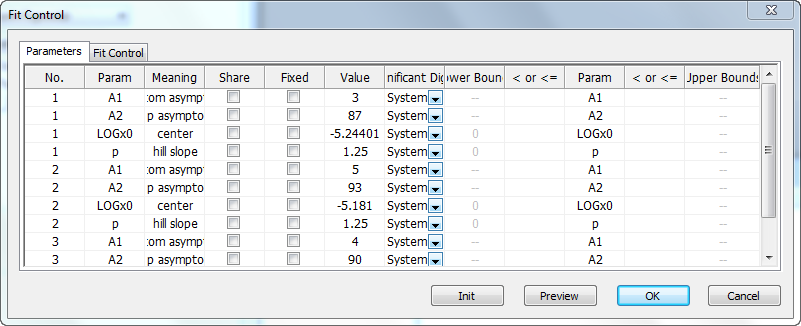
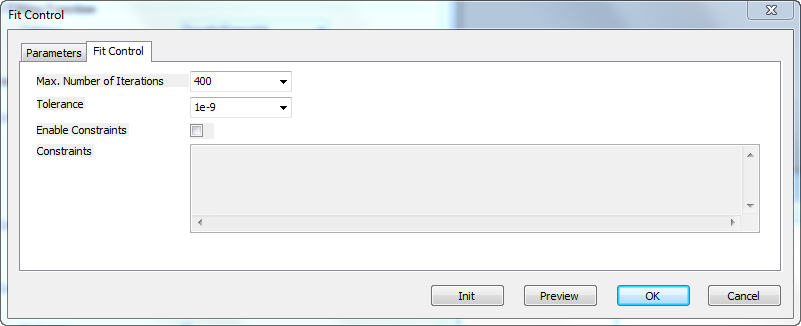
Fit Control tab

Max Number of Iterations	Specify the max number of iterations performed in fitting
Tolerance	Specify the tolerance in this combo-box. Fitting will be viewed as success if the reduced chi-square between two successive iterations is less than this tolerance value.
Enable Constraints	Specify whether to enable the constraints during fitting.
Constraints	Specify linear constraints for the fit parameters. The syntax for specifying constraints is same as with global fitting in the NLFit dialog. To refer to the parameters in the nth dataset, the "ParaName_n" notation should be used.

Buttons below the Panel

Init	Initialize the parameters with the parameter initialization codes (or initial values) in fdf file.
Preview	Update the preview graph using initial values in Parameters tab.

Algorithm

When comparing one specific parameter (or datasets), we are actually comparing two models. For one model, the parameter value can vary among different datasets, this is the more complicated model. For the other, the parameter values are assumed to be same for all datasets, this is the simpler model. When comparing a parameter, the more complicated model corresponds to independent fit for each dataset and the simpler model corresponds to global fit with the parameter shared.

When comparing datasets using a fit model, the more complicated model corresponds to independent fit for each dataset while the simpler model corresponds to a function with all parameters shared in all datasets.

Akaike Information Criteria(AIC)

For each model, Origin calculates the AIC value by:
$AIC=\left\{\begin{matrix} N\ln(\frac{RSS}{N})+2K & \mbox{when} \ \frac{N}{K}\geq 40\\ N\ln(\frac{RSS}{N})+2K+ \frac{2K(K+1)}{N-K-1} & \mbox{when} \ \frac{N}{K}< 40 \end{matrix}\right.$

where RSS is residual sum of squares for that model, N is the number of data points, K is the number of parameters.

For two fitting models, the one with the smaller AIC value is suggested to be a better model for the datasets, and then we can determine whether parameter values to be compared are same.

We can also make decisions based on the Akaike's weight value, which can be computed as:
$w_{i}=\frac{e^{-0.5AIC_{i}}}{e^{-0.5AIC_{1}}+e^{-0.5AIC_{2}}} \ \ \ i=1,2$
$w_{1}+w_{2}=1 \qquad 0<w_{1},w_{2}<1$
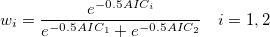
Here i=1 represents the simpler model and i=2 represents the more complicated model. $AIC_{1}$ and $AIC_{2}$ are the AIC values of the two fitting models, respectively.
If $w_{1}$ is larger than $w_{2}$ , we can conclude that parameter values to be compared are same, otherwise parameter values are different.

F-test

Suppose the sum of RSS and the sum of df (degrees of freedom) of the simpler model fit are $RSS_{1}, df_{1}$ and those of the more complicated model fit are $RSS_{2}, df_{2}$ .

We can compute the F value by:
$F=\frac{(RSS_{1}-RSS_{2})/(df_{1}-df_{2})}{RSS_{2}/df_{2}}$

Once the F value is computed, Origin calculates the P-value by:

$P=1-fcdf(F,df_{1}-df_{2},df_{2})$

This P-value can be used to determine whether parameter values to be compared are different. If the P-value is greater than 0.05, we can conclude that parameter values to be compared are not significantly different.

Skip Navigation Links

All Books