2.10.2 plot_BA
Menu Information
Bland-Altman
Brief Information
Create Bland-Altman plot
Additional Information
Minimum Origin Version Required: 2020b
Command Line Usage
1.plot_BA -r 1 irng:=[Book1]Sheet1!(C"RV",D"IC",A"Subj.") diff:=1 trplot.fillloa:=1 trplot.fillcil:=0;
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
irng
|
Input
Range
|
<active>
|
Specify data ranges of Method1, Method2, and Subject, in sequence. Subject column is optional.
Option list:
- Specify data column for the first method
- Specify data column for the second method
- Specify data column for Subject. This option is specified if your data has repeated measures for each subject. Your data will be grouped into subjects according to the Subject column you choose here. Multiple groups of subjects are supported.
|
| X Axis
|
xaxis
|
Input
int
|
Mean
|
Specify the values used for X axis.
Option list:
- mean:Mean
- m1:1st Method
- m2:2nd Method
- geo: Geometric
- Usually used when Y Axis is specified as ratios.
|
| Y Axis
|
yaxis
|
Input
int
|
1
|
Specify the values used for Y axis.
Option list:
- Difference / Mean X 100%
- This is the value used when Subject column is specified.
- Usually used when X Axis is specified as geo.
|
| SD Multiplier for LoA
|
sd
|
Input
double
|
1.96
|
Specify the multiplier factor of Standard Deviation for Limits of Agreement method.
|
| Confidence Level in %
|
conf
|
Input
double
|
95
|
Specify the confidence level in percentage.
|
| True Value is Constant
|
trueval
|
Input
int
|
0
|
Checking this option to use One Way Anova to get mean square for the residual for two methods separately. Available only when Subject is specified.
|
| Plot Each Subject as One Bubble
|
bubble
|
Input
int
|
1
|
Available only when Subject is specified. Specify whether to plot each subject as one bubble.
When it is selected, bubble size is mapped to number of replicates for each subject. Otherwise, each data point is plotted as one symbol, and its color and shape is mapped to Subject column.
|
| Mean Difference (bias) Estimation
|
diff
|
Input
int
|
Subject Difference
|
Available only when Subject is specified. When True Value is Constant is checked, Mean Difference Estimation uses subject differenct.
Option list:
- sub:Subject Difference
- indv:Individual Row
|
| Confidence Interval Estimation for LoA
|
interval
|
Input
int
|
MOVER
|
Available only when Subject is specified.
Option list:
- "mover:Mover
- delta:Delta Method
|
| Lines and Fills
|
trplot
|
Input
TreeNode
|
<unassigned>
|
Check to show the desired reference lines and color-filled area.
See details in the next table.
|
| Mean of Pairwise Means
|
mpm
|
Input
int
|
0
|
Mean of all pair-wise means: 0=false, 1=true.
|
| Bland-Altman Ratio
|
ratio
|
Input
int
|
0
|
Calculated as 0.5*(upper LoA - lower LoA)/mpm: 0=false, 1=true.
|
| Output Results
|
rd
|
Output
ReportData
|
[<input>]<new>
|
Specify the range of output data for plotting.
|
Details of Lines and Fills TreeNode
This trplot tree specifies all supported reference lines and filled intervals.
Syntax: trplot.Treenode:=<value>
Example: trplot.fillloa:=1
| Treenode
|
Label
|
Type
|
Default
|
Description
|
| mean
|
Mean
|
int
|
1
|
Line of Mean value.
|
| equality
|
Line of Equality (Difference=0)
|
int
|
1
|
Line of Equality (Difference=0).
|
|
|
Limits of Agreement
|
int
|
1
|
Limits of Agreement
|
| fillloa
|
Fill Between LoA
|
int
|
0
|
Fill interval area between LoA.
|
| cim
|
CI of Mean
|
int
|
0
|
Lines of upper and lower limits of confidence interval of mean. The confidence level is specified in Confidence Level in %.
|
| fillcim
|
Fill Between CI of Mean
|
int
|
1
|
Fill area between confidence interval of mean. The confidence level is specified by Confidence Level in %.
|
| cil
|
CI of Limits of Agreement
|
int
|
0
|
Lines of limits of Agreement
|
| fillcil
|
Fill Between CI of LoA
|
int
|
1
|
Fill area between confidence interval of limits of Agreement. The confidence level is specified by Confidence Interval Estimation for LoA.
|
Description
This X-Function is used to create the Bland-Altman plot. A Bland-Altman plot is a graphic display of difference between two methods. It is typically plotting the differences of two methods against their mean, with mean difference and 95% confidence intervals for comparison.
Also see menu deails here.
Algorithm
True Value Varies
It is assumed that the repeated differences for a single subject are independent in this case. One way ANOVA is used to calculate mean square of the residual (measurement error) for differences of two methers.

where 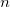 is the number of subjects, is the number of subjects, 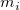 is number of observations on subject i. If all the subjects have the same number of observations, m, this factor reduces to m. is number of observations on subject i. If all the subjects have the same number of observations, m, this factor reduces to m.
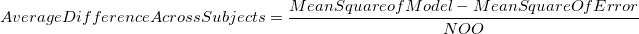
Total Variance for Single Differences on Different Subjects = Mean Square of Error + Average Difference across Subjects
Standard Deviation = Square Root of Total Variance for Single Differences on Different Subjects
Mean = mean of the individual differences
True Value is Constant
One Way Anova is used to get mean square for the residual (measurement error) for two methods separately.
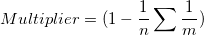
If the Multiplier of observations on each subjects are the same, the above formula can be simplified as:
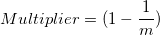
Standard Deviation = square root of (variance of differences between subject means + Multiplier of method1 * mean square of error of method1 + Multiplier of method2 * mean square of error of method2)
Mean = mean of the individual differences
References
Bland & Altman (2007)
|