2.13.1.8 grubbs
Menu Information
Statistics:Descriptive Statistics:Grubbs Test
Brief Information
Grubbs outlier test
Additional Information
Minimum Origin Version Required: 9.0 SR0
Menu accessible from 9.1 SR0
Command Line Usage
1. grubbs
2. grubbs ix:=col(2) alpha:=0.1
3. grubbs ix:=col(1) alpha:=0.05 box:=1
X-Function Execution Options
Please refer to the page for additional option switches when accessing the x-function from script
Variables
Display
Name
|
Variable
Name
|
I/O
and
Type
|
Default
Value
|
Description
|
| Input
|
ix
|
Input
vector
|
<active>
|
Must be a column or a range within a column
|
| Significance Level
|
alpha
|
Input
double
|
0.05
|
Option list:
|
| Data Point with Largest G
|
ox
|
Output
double
|
<unassigned>
|
The value of the suspected point
|
| Data Index with Largest G
|
index
|
Output
int
|
<unassigned>
|
Row index of suspected point
|
| G Test Statistic
|
gstat
|
Output
double
|
<unassigned>
|
The calculated G value from suspected point
|
| Critical Value
|
critical
|
Output
double
|
<unassigned>
|
The critical G value at the specified significance level
|
| Approximate P Value
|
pval
|
Output
double
|
<unassigned>
|
The p value for the test
|
| Test Significance
|
sig
|
Output
int
|
<unassigned>
|
sig=1 means there is an outlier, sig=0 means there is no outlier
|
| Conclusion
|
conclusion
|
Output
string
|
<unassigned>
|
A statement of conclusion indicating the statistical result
|
| Outlier Plot
|
box
|
Input
int
|
0
|
Specify whether to generate an outlier plot. box=1 means to generate, and box=0 means not to generate.
|
| Grubbs Plot Data
|
rd
|
Output
ReportData
|
[<input>]<new>
|
The worksheet range to put the plot data for outlier plot, if generating an outlier plot is selected.
|
| Grubbs Report
|
rt
|
Output
ReportTree
|
[<input>]<new>
|
The worksheet range to put the report table.
|
Description
Used to test outlier for a dataset with more than 3 data points, at significance level 0.01, 0.05 or 0.1.
Algorithm
1. Calculate G
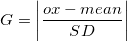
where ox is the value of suspected point (usually highest or lowest observation), mean is the mean value of data set, and SD is the standard deviation.
Compare G with the critical value.
2. Calculate p
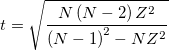
where Z is the largest G, N is the number of samples.
The p value is then calculated as the two-tailed P value for the student t distribution of the t value.
References
Stephen L R. Ellison, Vicki J. Barwick and Trevor J Duguid. Farrant. 2009. Practical Statistics for the Analytical Scientist. The Royal Society of Chemistry, Cambridge, UK.
Related X-Functions
qtest
Keywords:significance level
|