Parameterinitialisierung für rationale Funktionen
RationalFunc-InitialParameter
Zusammenfassung
In diesem Tutorial sehen Sie, wie Initialisierungsparameter für rationale
Fitfunktionen mit Hilfe der multiplen linearen Regression berechnet werden
und ein Fit der Daten mit diesen berechneten Parametern durchgeführt wird.
Origin-Version mind. erforderlich: Origin 9.0 SR0
Was Sie lernen
werden
Dieses Tutorial zeigt Ihnen, wie Sie:
- Initialisierungsparameter für rationale Fitfunktionen berechnen.
- eine multiple lineare Regression mit Hilfe von Origin C-Code durchführen.
Beispiel und
Schritte
Algorithmus
In diesem Tutorial wird die folgende rationale Funktion als Beispiel
verwendet:
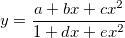
wobei x die unabhängige Variable und y die abhängige Variable
ist sowie a, b, c, d, e die Fitparameter
sind.
Das Multiplizieren beider Seiten mit dem Nenner der rechten Seite ergibt:
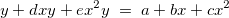
, und die Gleichung kann ausgedrückt werden mit:
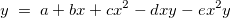
Das Substituieren der Anpassungsdaten 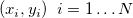 in der Gleichung ergibt: in der Gleichung ergibt:
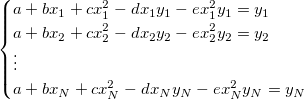
Daher wird das Schätzen der Initialisierungsparameter für eine rationale
polynomielle Fitfunktion ein Problem für die multiple lineare Regression
mit den linearen Koeffizienten a, b, c, d,
e.
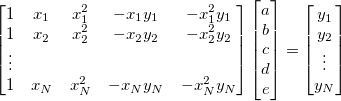
Für die multiple lineare Regression enthält Origin eine Funktion ocmath_multiple_linear_regression
in Origin C, die über den Initialisierungscode aufgerufen werden kann.
Daten importieren
- Öffnen Sie eine neue Arbeitsmappe.
- Kopieren Sie die Daten unter Beispieldaten
in die Arbeitsmappe.
- Markieren Sie Spalte B und wählen Sie Zeichnen: Symbol: Punktdiagramm
im Origin-Menü. Das Diagramm sollte folgendermaßen aussehen:
-
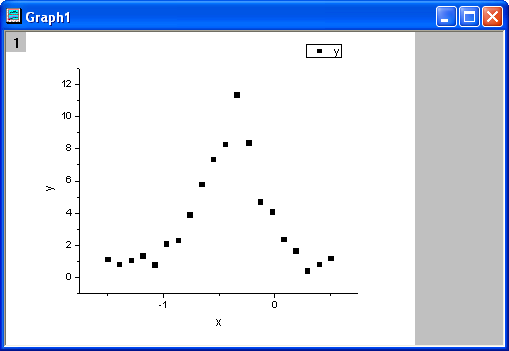
Fitfunktionen definieren und Parameter initialisieren
Die Anpassungsfunktion kann mit Hilfe des Hilfsmittels Fitfunktionen
erstellen definiert werden.
- Wählen Sie Hilfsmittel: Fitfunktionen erstellen im Origin-Menü.
- Klicken Sie im Dialog Fitfunktionen erstellen auf der Seite
Ziel auf die Schaltfläche Weiter.
- Wählen Sie auf der Seite Name und Typ die Option User
Defined in der Auswahlliste Eine Kategorie auswählen oder erstellen,
geben Sie rationalfunc im Feld Funktionsname ein und wählen
Sie Ausdruck in der Gruppe Funktionstyp. Klicken Sie auf
die Schaltfläche Weiter.
- Geben Sie auf der Seite Variablen und Parameter die Parameter
a, b, c, d, e in das Feld Parameter ein. Klicken Sie auf
die Schaltfläche Weiter.
-
Geben Sie auf der Seite Ausdrucksfunktion das folgende Skript
im Feld Funktionskörper ein:
(a+b*x+c*x^2)/(1+d*x+e*x^2)
Klicken Sie auf die Schaltfläche Auswerten. Es wird y=1 bei
x=1 gezeigt, das heißt, der Ausdruck ist korrekt. Klicken Sie auf die
Schaltfläche Weiter.
-
Klicken Sie auf der Seite Parameterinitialisierungscode auf
die Schaltfläche Code Builder öffnen
 rechts neben dem Feld Initialisierungscode und initialisieren
Sie die Fitparameter, wie folgt, entsprechend dem Algorithmus. rechts neben dem Feld Initialisierungscode und initialisieren
Sie die Fitparameter, wie folgt, entsprechend dem Algorithmus.
UINT nOSizeN = x_data.GetSize(); //Number of points
UINT nVSizeM = 5; //Number of parameters
matrix mX(nOSizeN, 5);
//Construct matrix for data points of independent variables
vector vCa(nOSizeN), vCb, vCc, vCd, vCe;
vCa = 1;
mX.SetColumn( vCa, 0 );
vCb = x_data;
mX.SetColumn( vCb, 1 );
vCc = x_data^2;
mX.SetColumn( vCc, 2 );
vCd = -x_data*y_data;
mX.SetColumn( vCd, 3 );
vCe = -x_data^2*y_data;
mX.SetColumn( vCe, 4 );
//Options for multiple linear regression
LROptions stLROptions;
stLROptions.UseReducedChiSq = 1;
stLROptions.FixIntercept = 1; //Fix the intercept at 0.
FitParameter stFitParameters[ 6 ]; // should be nVSizeM+1
UINT nFitSize = nVSizeM + 1;
int nRet = ocmath_multiple_linear_regression(mX, nOSizeN, nVSizeM, y_data,
NULL, 0, &stLROptions, stFitParameters, nFitSize );
if( nRet == STATS_NO_ERROR )
{
a = stFitParameters[1].Value;
b = stFitParameters[2].Value;
c = stFitParameters[3].Value;
d = stFitParameters[4].Value;
e = stFitParameters[5].Value;
}
Klicken Sie auf die Schaltfläche Kompilieren, um die Datei
zu kompilieren. Klicken Sie dann auf die Schaltfläche Zurück zum NSLF.
Klicken Sie auf die Schaltfläche Fertigstellen, um den Dialog Fitfunktionen
erstellen zu schließen.
Kurve anpassen
- Wählen Sie Analyse: Anpassen: Nichtlinearer Fit im Origin-Menü.
Wählen Sie im Dialog NLFit auf der Seite Einstellungen: Funktionsauswahl
die Option User Defined in der Auswahlliste Kategorie und
die Funktion rationalfunc in der Liste Funktion.
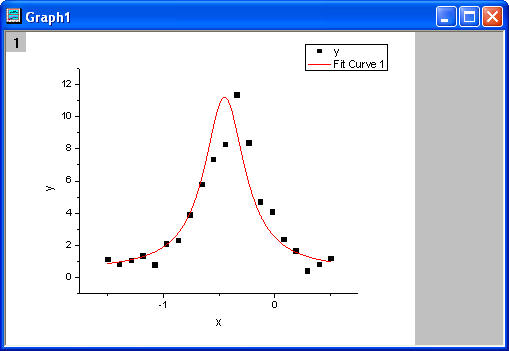
- Aktivieren Sie die Registerkarte Parameter. Die aus dem
Initialisierungscode berechneten Initialisierungsparameter werden im Dialog
aufgelistet, und die Fitfunktionskurve für die Parameter wird folgendermaßen
gezeigt. Es scheint, dass die Initialisierungsparameter aus dem Initialisierungscode
sehr gut sind.
- Klicken Sie auf die Schaltfläche Fit, um die Kurve anzupassen.
Anpassungsergebnisse
Die angepasste Kurve sollte folgendermaßen aussehen:
-
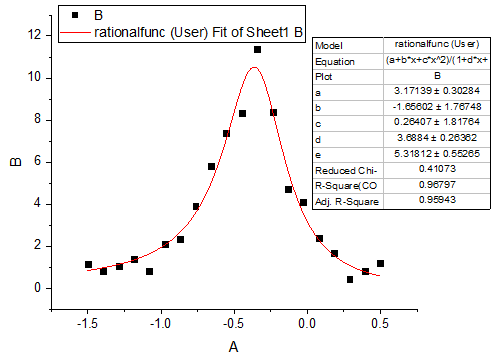
Die angepassten Parameter sind im Folgenden zu sehen:
| Parameter |
Wert |
Standardfehler |
|---|
| a |
3,17139 |
0,30284 |
|---|
| b |
-1,65602 |
1,76748 |
|---|
| c |
0,26407 |
1,81764 |
|---|
| d |
3,6884 |
0,26362 |
|---|
| e |
5,31812 |
0,55265 |
|---|
Beispieldaten
| x |
y |
|---|
| -1,5 |
1,13173 |
| -1,39474 |
0,8262 |
| -1,28947 |
1,06999 |
| -1,18421 |
1,37155 |
| -1,07895 |
0,79569 |
| -0,97368 |
2,11346 |
| -0,86842 |
2,32006 |
| -0,76316 |
3,9205 |
| -0,65789 |
5,81904 |
| -0,55263 |
7,38037 |
| -0,44737 |
8,31272 |
| -0,34211 |
11,39718 |
| -0,23684 |
8,39808 |
| -0,13158 |
4,7305 |
| -0,02632 |
4,11105 |
| 0,07895 |
2,39105 |
| 0,18421 |
1,65394 |
| 0,28947 |
0,42953 |
| 0,39474 |
0,83337 |
| 0,5 |
1,18758 |
| Hinweis: Sie können diese Methode
auch verwenden, um Parameter für andere rationale polynomielle Fitfunktionen
zu initialisieren. |
|