Einfache ANOVA mit wiederholten Messungen

1WayRepeatedMeasuresANOVA

Zusammenfassung

Die einfache ANOVA bei wiederholten Messungen ähnelt der einfachen ANOVA, verarbeitet jedoch eine abhängige Variable, die wiederholten Messungen unterliegt. In dieser Situation ist die Annahme der Unabhängigkeit der allgemeinen einfachen ANOVA nicht vertretbar, da es wahrscheinlich eine Korrelation zwischen den Stufen des wiederholten Faktors gibt.

Wie die einfache ANOVA kann die einfache ANOVA mit wiederholten Messungen herangezogen werden, um zu testen, ob Mittelwerte gleich sind oder nicht. Diese Mittelwerte schließen den Mittelwert unterschiedlicher Messungen und den Mittelwert unterschiedlicher Objekte ein. Diese Ergebnisse werden in der Tabelle mit dem Titel Test auf Effekte innerhalb der Versuchsobjekte bzw.Test auf Effekte zwischen den Versuchsobjekten ausgegeben. Beachten Sie, dass die ANOVA bei wiederholten Messungen in Origin balancierte Sampledaten benötigt, das heißt den gleichen Stichprobenumfang auf jeder Stufe.

Origin-Version mind. erforderlich: 8.6 SR0

Was Sie lernen werden

Dieses Tutorial zeigt Ihnen, wie Sie:

• indizierte Daten in den Dialog der statistischen Analyse eingeben.
• die einfache ANOVA mit wiederholten Messungen durchführen,
• die Ergebnisse einer einfachen ANOVA bei wiederholten Messungen interpretieren.

Schritte

Origin kann eine einfache ANOVA mit wiederholten Messungen sowohl für indizierte als auch für Rohdaten durchführen. Wenn für die einfache ANOVA mit wiederholten Messungen der Indexmodus verwendet wird, sollten die Daten in drei Spalten organsisiert sein: Faktor, Daten und Subjekt. Wenn der Rohdatenmodus verwendet wird, sollten sich die verschiedenen Stufen in verschiedenen Spalten befinden.

Datenmodus Indiziert

Die Daten enthalten Messungen für 3 verschiedene Dosen von 20 Subjekten. Unser Interesse besteht darin herauszufidnen, ob die verschiedenen Dosen unterschiedliche Effekte auf die Subjekte haben. Um dies zu testen, führen wir eine einfache ANOVA mit wiederholten Messungen durch, wobei wir indizierte Daten verwenden.

1. Öffnen Sie ein leeres Arbeitsblatt. Wählen Sie Hilfe: Ordner öffnen: Sample-Ordner ... im Menü, um den Ordner "Samples" zu öffnen. Öffnen Sie in diesem Ordner den Unterordner Statistics. Dort befindet sich die Datei One Way_RM_ANOVA_indexed.dat. Ziehen Sie diese Datei per Drag&Drop in das leere Arbeitsblatt, um sie zu importieren.
2. Wählen Sie Statistik: ANOVA: Einfache ANOVA mit wiederholten Messungen, um den Dialog zu öffnen. Wählen Sie auf der Registerkarte Eingabe dieses Dialogs die Option Indiziert in der Auswahlliste Eingabedaten und setzen Sie die Spalten B(dose), C(Data) und A(Subject) auf Faktor, Daten bzw. Subjekt.

   

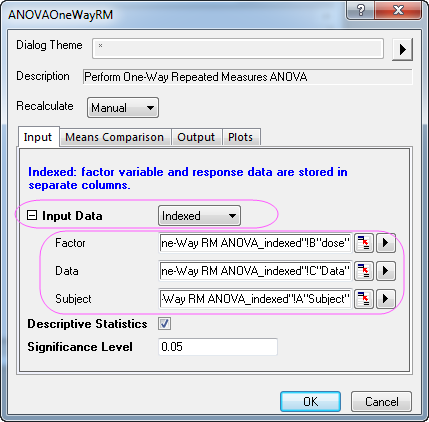
3. Wechseln Sie zur Registerkarte Mittelwertevergleich und aktivieren Sie das Kontrollkästchen vor Bonferroni, um den Bonferroni-Test zu aktivieren.

   

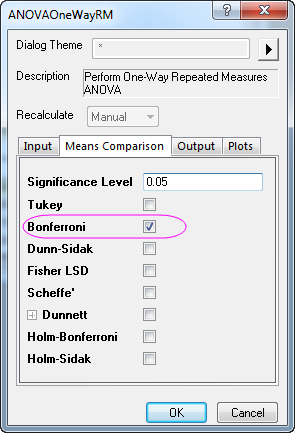
4. Aktivieren Sie die Kontrollkästchen Mittelwertdiagramm (SE als Fehler) und Mittelwertvergleichsdiagramm auf der Registerkarte Diagramme.

   

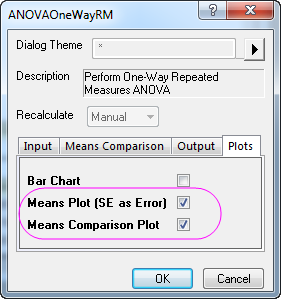
5. Klicken Sie auf OK, um die Analyse durchzuführen.

Interpretation der Ergebnisse

Go to the worksheet ANOVAOneWayRM1, where the analysis results are listed.

Sie können dieses Kapitel der Hilfe verwenden, um die Ergebnisse der ANOVA mit wiederholten Messungen zu interpretieren.

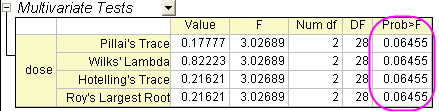
Origin druckt die MANOVA automatische mit den wiederholten Messungen aus, um deren Effekte zu erkennen. Beachten Sie, dass die vier verschiedenen Methoden (Pillai-Spur, Wilks' Lambda, Hotelling-Spur und die größte charakteristische Wurzel nach Roy) identische F-Statistiken und Wahrscheinlichkeiten, P=0,06455, erzeugen, so dass die Mittelwerte unter den Bedingungen der drei Stufen statistisch nicht unterschiedlich sind. Vergleichen Sie dies mit dem folgenden Bericht der ANOVA . Wir können sehen, dass die Schlussfolgerung konservativ ist.

Diese Tabelle zeigt die Ergebnisse des Mauchly-Test (Sphärizitätstest). Aus den Testergebnissen können wir ersehen, dass die Sphärizität hält. Von Interesse ist in diesem Fall der Wert von Wahrsch. > Chi-Qdr, der das Signifikanzniveau des Mauchly-Tests darstellt. Aus diesem Beispiel können wir ersehen, dass das Signifikanzniveau (0,44609) größer als 0,05 ist. Daher wurde die Annahme der Sphärizität nicht verletzt.

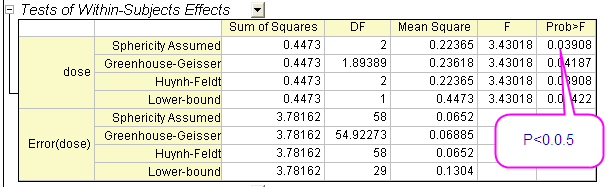
Diese Tabelle stellt den F-Wert für den Faktor zusätzlich zu dem zugehörigen Signifikanzniveau und der Effektgröße bereit. Da unsere Daten der Annahme der Sphärizität folgen, können wir schlussfolgern, dass die Mittelwerte unter den Bedingungen der drei Stufen statistisch unterschiedlich sind (P = 0,03908 < 0.05), wenn eine ANOVA mit wiederholten Messungen und angenommener Sphärizität verwendet wird. Mit anderen Worten: die Dosis ist ein signifikanter Faktor.

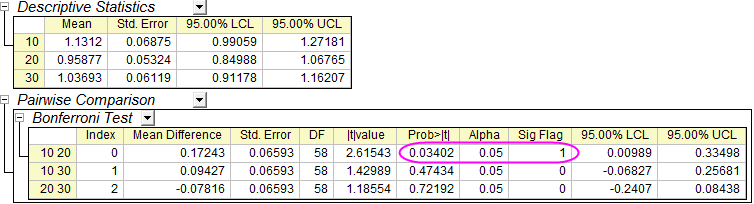
Die in der vorherigen Tabelle dargestellten Ergebnisse haben gezeigt, dass es eine signifikante Gesamtdifferenz unter den Mittelwerten gibt, wir jedoch nicht wissen, wodurch diese Differenzen verursacht werden. Diese Tabelle zeigt die Ergebnisse des Bonferroni-Tests, der ersichtlich macht, welche speziellen Mittelwerte sich unterscheiden. In diesem Fall haben die Mittelwerte von Dose = 10 und Dose = 20 eine signifikante Differenz (P = 0,03402 < 0,05 und Sig Flag = 1).

Von den beiden Zeichnungen unten ausgehend können wir leicht zu der gleichen Schlussfolgerung kommen.
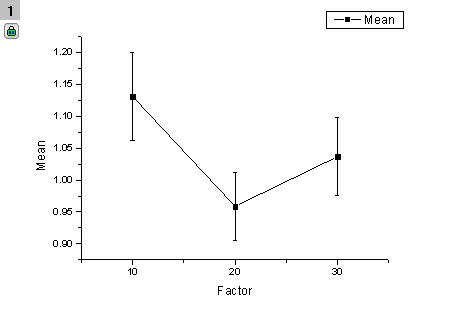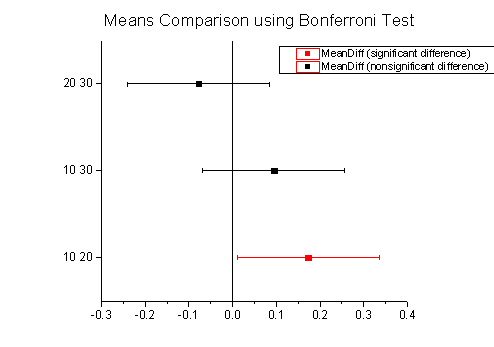