Algorithmus (Hierarchische Clusteranalyse)
Die hierarchische Clusteranalyse wird verwendet, um einen hierarchischen Baum zu erstellen. Zu Beginn gibt es n Cluster, jeder mit einem einzelnen Objekt und dann auf jeder n ? 1 Stufen werden zwei Cluster zusammengefügt und bilden einen größeren Cluster, bis sich alle Objekte in einem einzigen Cluster befinden. Der Vorgang kann in einem Dendrogramm gezeigt werden.
Die zu clusternden Objekte in der hierarchischen Clusteranalyse können Beobachtungen oder Variablen sein.
Distanzmatrix
Eine Distanz- oder Unähnlichkeitsmatrix ist eine symmetrische Matrix mit null diagonalen Elementen. Das ij-te Element stellt dar, wie unähnlich sich das i-te und j-te Objekt sind. Die Methoden zum Berechnen der Distanz zwischen zwei Objekten unterscheiden sich je nach dem, ob Beobachtungen oder Variablen geclustert werden.
Beobachtungen clustern
Origin unterstützt die Standardisierung von Daten vor der Distanzberechnung zum Clustern von Beobachtungen. Beobachtungen, die einen oder mehrere fehlende Werte enthält, werden aus der Analyse ausgeschlossen.
- Variablen standardisieren
- Normieren auf N(0,1)
Eine Variable 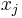 wird normiert zu: wird normiert zu: 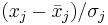 , wobei , wobei 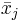 und und 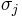 der Mittelwert und die Standardabweichung der Variable sind. Die standardisierte Variable hat einen Mittelwert bei Null und eine einheitliche Standardabweichung. der Mittelwert und die Standardabweichung der Variable sind. Die standardisierte Variable hat einen Mittelwert bei Null und eine einheitliche Standardabweichung.
- Normieren auf (0,1)
Eine Variable 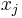 wird normiert zu: wird normiert zu: 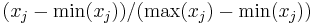 . Die Variable wird im Bereich 0 bis 1 standardisiert. . Die Variable wird im Bereich 0 bis 1 standardisiert.
Origin unterstützt drei Distanztypen.
- Distanztyp
Für eine standardisierte Matrix 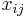 mit n Beobachtungen und p Variablen kann die Distanz zwischen der i-ten Beobachtung und der k-ten Beobachtung folgendermaßen ausgedrückt werden: mit n Beobachtungen und p Variablen kann die Distanz zwischen der i-ten Beobachtung und der k-ten Beobachtung folgendermaßen ausgedrückt werden:
- Euklidische Distanz
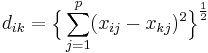
- Quadrierte euklidische Distanz
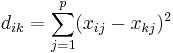
- Absolute Distanz (City-Block-Metrik)
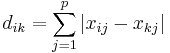
- Kosinus-Distanz
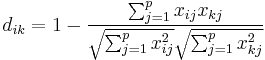
- Pearson-Korrelationsdistanz
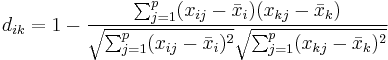
, wobei 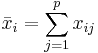 und und 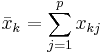
- Jaccard-Distanz
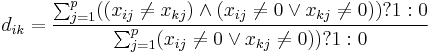
Variablen clustern
Origin unterstützt zwei Distanztypen zum Clustern von Variablen. Beobachtungen werden aus der Berechnung der Korrelation zwischen zwei Variablen ausgeschlossen, wenn fehlende Werte in einer der beiden Variablen existieren.
- Distanztyp
Für eine Matrix 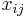 mit n Beobachtungen und p Variablen kann die Distanz zwischen der j-ten Variablen und der k-ten Variablen folgendermaßen ausgedrückt werden. mit n Beobachtungen und p Variablen kann die Distanz zwischen der j-ten Variablen und der k-ten Variablen folgendermaßen ausgedrückt werden.
- Korrelation
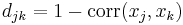 wobei wobei 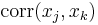 die Korrelation zwischen der j-ten Variablen und der k-ten Variable ist. die Korrelation zwischen der j-ten Variablen und der k-ten Variable ist.
- Absolute Korrelation
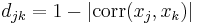
Verknüpfungsmethode
Auf jeder Stufe werden die beiden Cluster, die sich am nahesten sind, zusammengefügt. Origin bietet mehrere Methoden, um die Distanz zwischen dem neuen und den anderen Clustern zu berechnen. Die zwei Cluster j und k werden zu dem Cluster jk zusammengefügt. 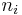 , , 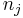 und und 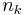 seien die Anzahl der Objekte von Cluster i, Cluster j und Cluster k und seien die Anzahl der Objekte von Cluster i, Cluster j und Cluster k und 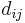 , , 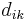 und und 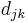 seien die Distanzen zwischen zwei Clustern. Die Distanz zwischen Cluster jk und Cluster i seien die Distanzen zwischen zwei Clustern. Die Distanz zwischen Cluster jk und Cluster i 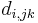 kann dann folgendermaßen berechnet werden: kann dann folgendermaßen berechnet werden:
- Einzelne Verknüpfung oder Nächster Nachbar
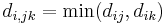
- Vollständige Verknüpfung oder Weitesten entfernter Nachbar
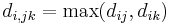
- Gruppendurchschnitt
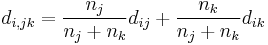
- Zentroid
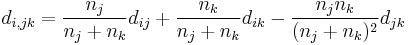
- Median
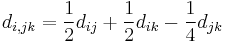
- Minimale Varianz oder Ward
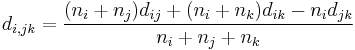
Wenn Cluster j und k, j<k, zusammengefügt werden, wird der neue Cluster in der Tabelle der Clusterstufen als Cluster j bezeichnet.
Dendrogramm
Das Dendrogramm ist ein hierarchischer Baum, der zeigt, bei welcher Distanz zwei Cluster zusammengefügt werden. Jede Stufe wird durch eine Einheit in dem Dendrogramm dargestellt. Der obere Teil der Einheit für jede Stufe stellt den neuen Cluster dar, indem zwei Cluster zusammengefügt wurden. Die Höhe entspricht der Distanz zwischen den zwei zusammengefügten Clustern.
Die Endpunkte des Dendrogramms stellen n Objekte dar. Die n Objekte in dem Dendrogramm werden sortiert, so dass die Cluster, die zusammengefügt wurden, nebeneinander liegen. Der erste Endpunkt im Dendrogramm entspricht immer dem ersten Objekt.
Objekte gruppieren
Die Zugehörigkeit von n Objekten für festgelegte k Cluster kann mit den Informationen aus dem Dendrogramm oder der Tabelle der Clusterstufen bestimmt werden. k Cluster befinden sich auf der n-k-ten Stufe, das heißt, die Zugehörigkeit von jedem Objekt ist durch die ersten n-k-ten Stufen bekannt. Objekt 1 gehört immer zu Cluster 1.
Clusterzentren, die Distanz zwischen Clusterzentren und die Distanz zwischen Beobachtungen und Clustern werden zum Clustern von Beobachtungen berechnet. Beachten Sie, dass Beobachtungen in der Berechnung standardisiert sind, wenn die Standardisierung in der Analyse gewählt wird.
|