OriginPro in Studies of Microwave Signal Frequency Dynamics
Problem
To analyze a microwave signal's frequency dynamics during the generated microwave pulse.
Solution
Use Origin to perform Short-time Fourier Transform (STFT) on the microwave signal during the pulse, to see how the frequency of the output signal is changed.
“The most important aspects ... are Origin’s capabilities in signal analyzing.”
The magnetron is a device first developed and studied in the early 1920s. Most credit Albert Hull at General Electric with the development of the device he called the “magnetron” though others independently researched and developed similar devices. A.L. Samuel at Bell Labs is often credited with developing the multi-cavity magnetron. However, the first truly successful example of a multi-cavity magnetron was developed by Nikolay Alekseev and Dmitriy Malyarov in Russia in 1936, which achieved 300 watts at 3 GHz. In 1940, British engineers John Randall and Henry Boot developed a more sophisticated multi-cavity magnetron that increased the electromagnetic wave generating capabilities of the device, enabling British forces to gain an advantage in the detection of German submarines. Subsequently, the British established an information exchange program with American scientists, leading to the first mass production of the magnetron. Today, cavity magnetrons have practical applications including, but not limited by radar transmitters and microwave ovens.
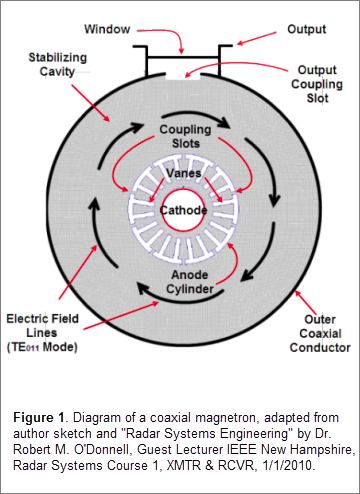
The magnetron’s purpose is to generate electromagnetic waves in the millimeter to decimeter range. A modern cavity magnetron is an evacuated tube that operates by applying a voltage between a cathode at the center of the magnetron and an anode. A cylindrical anode surrounds the cathode and this anode contains several precisely-shaped cavities, arrayed around the interior of the anode. Electrons generated at the cathode move along a circular path around the interior of the anode, causing the shaped cavities to resonate as they pass, thus producing electromagnetic waves. This generated electromagnetic radiation is then channeled by an output waveguide into the air by means of an antenna or other output electromagnetic power structure [1].
“Origin allows me to save my time by collecting and analyzing big amounts of data produced in both simulations and experiments, and preparing results on the analysis for presentations and publications”
Dr. Andrey D. Andreev, Lead Engineer at Booz Allen Hamilton Inc., conducts research into the physics of magnetron operation. He was kind enough to share results of a recent simulation and analysis study of the S-band coaxial VMS-1143B magnetron, manufactured by Communication & Power Industries’ Beverly Microwave Division. The VMS-1143B magnetron employs a “coaxial” design (Figure 1) that is characterized by the presence of a “stabilizing cavity” between the anode and the output waveguide. According to the manufacturer, the stabilizing cavity significantly improves the performance of the magnetron by allowing a greater number of resonators, decreasing the tendency for arcing at the vane tips, and improving spectrum quality and tuning capabilities. The VMS-1143B and its predecessors have 40 years of proven reliability in civilian and military radar applications, worldwide. In typical applications, the VMS-1143B provides up to 3 megawatts (MW) of microwave power in the S-band of microwave spectra (2 – 4 gigahertz (GHz)), at an anode voltage of 65 kilovolts (kV) and an anode current of 100 amps (A). The VMS-1143B can be mechanically tuned to an operational frequency range of 2.7 – 2.9 GHz and has a demonstrated service life of over 100,000 hours [2]. Interestingly, Dr. Andreev points out, one application of the VMS-1143B has been its use as a driving source to facilitate operation of a more powerful 60 MW VMS-1873B magnetron [3].
Dr. Andreev states that “a primary characteristic of a resonant system of a multi-cavity magnetron is the Brillouin dispersion diagram, which links the resonant frequencies (fr) of a certain number n, of electromagnetic (EM) modes (resonances), possible within the resonant system, and the phase shifts (ΔΦnm) (per single spatial period of the resonant system) of the space harmonics (nm) (associated with the components m of the EM mode n) of the non-sinusoidal EM wave azimuthally traveling around the circumference of the resonant system. Thus, the Brillouin dispersion diagram shows the phase shifts or the phase differences per cavity (Δφnm’) of that space harmonics nm of the induced EM electric field E1, whose spatial configurations at certain resonant frequencies fr, within the given resonant system define each component m of each EM mode n.”
The example Brillouin diagrams of the VMS-1873B magnetron with and without stabilizing cavity that Dr. Andreev provided seemed to show that the stabilizing cavity produced a more complex dispersion diagram and Dr. Andreev confirmed: “The stabilizing cavity certainly complicates a dispersion diagram and, sometime but not always, leads to generation of a more complex signal, such as a mixture of two magnetron modes. While this certainly complicates understanding of a magnetron operation, it makes the magnetron more effective and productive in terms of the microwave output power generation” [5].
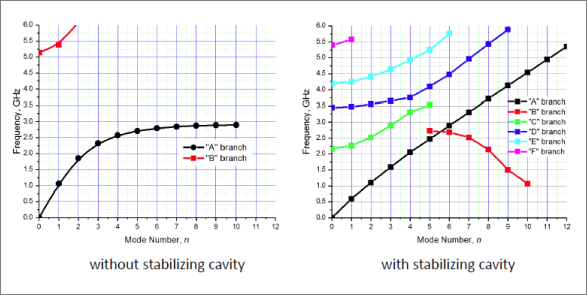
Figure 2: Brillouin dispersion diagrams of a coaxial magnetron without (left) and with (right) stabilizing cavity [5].
Dr. Andreev’s study of the VMS1143B magnetron entailed performing “cold” and “hot” simulations of magnetron operation, using three different computer codes, LANL's Poisson Superfish and ANSYS HFSS for “cold” simulations and AFRL's ICEPIC for “hot” simulations. Dr. Andreev explains that “cold” simulations are computer simulations without an electron beam (flow) inside of the slow-wave structure. “Hot” computer simulations are, respectively, simulations with an electron beam (flow) involved. Dr. Andreev’s study showed, for example, that there was close agreement between results produced by the 2D “cold” Superfish model (LANL's Poisson Superfish) simulations and the 3D cold HFSS (ANSYS' HFSS) simulations: “Yes, the 2D “cold” simulations produce the same results as the 3D cold simulations, when the results of the 2D “cold” simulations are analytically recalculated to a 3D “cold” geometry.”
The preliminary ”hot” 3D ICEPIC (particle-in-cell) simulations showed, however, that an anode current was almost three times higher than the VMS1143B rated anode current of 100 A and that output microwave power was 20% less than the VMS1143B rated power output of 3 MW at about the same anode voltage of 65kV. Dr. Andreev explains this discrepancy by the fact that while the actual VMS1143B magnetron operates in secondary electron emission mode, the ICEPIC simulations are done assuming the space-charge limiting electron emission mode. “Usually, space-charge limited electron emission produces much more electron current that the secondary electron emission does. This might be an actual reason for an observed discrepancy in the anode current and in the output microwave power. However, this needs to be proved in computer simulations, which are not done yet,” Dr. Andreev states.
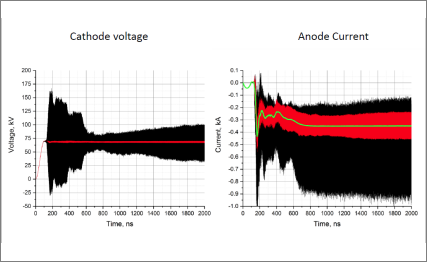
Figure 3: Hot 3D ICEPIC Magnetron Simulation and Analysis Results: 70kV X 0.23T
|
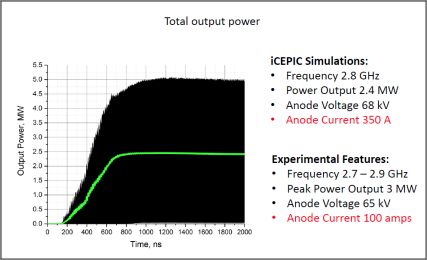
Figure 4: Hot 3D ICEPIC Magnetron Simulation and Analysis Results: 70kV X 0.23T
|

Figure 5: Hot 3D ICEPIC Magnetron Simulation and Analysis Results: 70kV X 0.23T, RF oscillations inside one of the resonators.
|

Figure 6: Hot 3D ICEPIC Magnetron Simulation and Analysis Results: 70kV X 0.23T, RF oscillations inside the stabilizing cavity.
|
References:
[1] Cavity Magnetron.
[2] S-Band 3 MW Coaxial Magnetron (PDF).
[3] T.A. Treado, R.A. Bolton, T.A. Hansen, P.D. Brown, and J.D. Barry, “High-power, high-efficiency, injection-locked secondary-emission magnetron", IEEE Transactions on Plasma Science, Vol. 20, No. 3, June 1992, pp. 351-359.
[4] A.D. Andreev, K.J. Hendricks, S. Soh, M. Fuks, and E. Schamiloglu, “Elemental theory of a relativistic magnetron operation: Dispersion diagram", Journal of Directed Energy, Vol. 5, No. 1, Spring of 2013, pp. 1-41.
[5] Andrey D. Andreev, and Chris Walker, ”Computer Simulations of a Megawatt-class S-Band Coaxial Magnetron”, presented at 44th International Conference on Plasma Science, Atlantic City, New Jersey, May 21 - 25, 2017.