NAGライブラリを使った積分フィット
Fitting-Integral-NAG
サマリー
Originで、積分を求めるOrigin Cフィット関数を定義することができます。NAG関数を呼び出し、積分を実行するようにフィット関数を定義します。積分を実行する組込のOrigin C関数があります。ここでのサンプルでは、NAG関数を使用する方法をお薦めします。組込の積分のアルゴリズムに比べ、パフォーマンスが優れているためです。ここでは有限NAG統合が使用されています。
必要なOriginのバージョン:8.0 SR6
学習する項目
このチュートリアルでは、以下の項目について説明します。
- フィット関数オーガナイザでフィット関数を作成する
- NAGの積分ルーチンを使って、定積分でのフィット関数を作成する
- フィット関数の初期化コードをセットアップする
サンプルとステップ
次のモデルをフィットします。
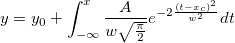
ここで 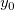 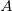 , , 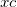 および および 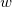 は、データフィットから取得したいモデルのパラメータです。フィットの手順は、次のステップに沿って行います。 は、データフィットから取得したいモデルのパラメータです。フィットの手順は、次のステップに沿って行います。
関数を定義する
F9 を押し、フィット関数オーガナイザを開き、 FittingWithIntegralという名前の新しいカテゴリーを作成します。このカテゴリーに、新しいフィット関数 nag_integration_fitting を以下のように定義します。
-
| 関数名: |
nag_integration_fitting |
| 実現方式: |
ユーザ定義 |
| 独立変数: |
x |
| 従属変数: |
y |
| パラメータの名前: |
y0, A, xc, w |
| 定義形式: |
Origin C |
| 関数: |
|
関数ボックスの近くにある ボタンをクリックしてコードビルダを開き、次のように操作します。 ボタンをクリックしてコードビルダを開き、次のように操作します。
- スクロールして次の行まで移動します。
//add the header file for the NAG functions here.
そして、以下のコードをこの行の下に貼り付けます。
#include <oc_nag8.h>
- 次の行まで行きます。
// and access in your fitting function.
そして、以下のコードをこの行の下に貼り付けます。
struct user // 被積分関数のパラメータ
{
double amp, center, width;
};
// ユーザによって定義された関数は、与えられたxで被積分関数の値を返します。
static double NAG_CALL f_callback(double x, Nag_User *comm)
{
struct user *sp = (struct user *)(comm->p);
double amp, center, width; // Nag_User構造体でのパラメータを受け付ける一時的な変数
amp = sp->amp;
center = sp->center;
width = sp->width;
return amp * exp( -2*(x - center)*(x - center)/width/width ) / (width*sqrt(PI/2));
}
- 次の行まで行きます。
// Beginning of editable part.
そして、以下のコードをこの行の下に貼り付けます。
// epsabsは絶対精度、epsrelおよびmax_num_subintは相対精度であり、
// 必要な積分の精度を制御できます。
// epsrelが負にセットされている場合、絶対精度が使われます。
// 同様に、epsabs を負にセットすることで、相対精度のみを制御することもできます。
double epsabs = 0.0, epsrel = 0.0001;
// 積分で関数を評価するのに必要なsub-intervalsの最大数
// より複雑な被積分関数にると、max_num_subintも大きくなります。
// ほとんどの問題に対しては、200から500くらいが適切であり、お薦めです。
Integer max_num_subint = 200;
// 結果はアルゴリズムによって返される適切な積分値を持ちます。
// abserrは、|I - result|に対する上側境界であるエラーの推測です。
// ここで、Iは整数値です。
double result, abserr;
// Nag_QuadProgressの構造体
// これには、max_num_subint 要素への内部的なメモリアロケーションへのポインタが含まれます。
Nag_QuadProgress qp;
// NAG エラーパラメータ(構造体)
static NagError fail;
// Nag_User構造体によって、パラメータが被積分関数に渡されます。
Nag_User comm;
struct user s;
s.amp = A;
s.center = xc;
s.width = w;
comm.p = (Pointer)&s;
// 積分実行
// Nag無限積分器で使うことができる無限の境界は3種類あります。
// Nag_LowerSemiInfinite, Nag_UpperSemiInfinite, Nag_Infinite
d01smc(f_callback, Nag_LowerSemiInfinite, x, epsabs, epsrel, max_num_subint, &result, &abserr, &qp, &comm, &fail);
// エラーメッセージを出力することで、エラーを調査するには、以下の行のコメントを解除します。
// if (fail.code != NE_NOERROR)
// printf("%s\n", fail.message);
// 次の3つのエラー以外は、入力パラメータが不正であるか
// アロケーションエラーに当たります。 NE_INT_ARG_LT NE_BAD_PARAM NE_ALLOC_FAIL
// メモリーリークを避けるため、積分ルーチンを呼ぶ前にメモリのアロケーションを解放する必要があります。
if (fail.code != NE_INT_ARG_LT && fail.code != NE_BAD_PARAM && fail.code != NE_ALLOC_FAIL)
{
NAG_FREE(qp.sub_int_beg_pts);
NAG_FREE(qp.sub_int_end_pts);
NAG_FREE(qp.sub_int_result);
NAG_FREE(qp.sub_int_error);
}
// フィット値の計算
y = y0 + result;
- コンパイルボタンをクリックしてファイルをコンパイルします。
上記のコードでは、フィット関数 _nlsfnag_integration_fittingの本体の外側で、最初に被積分関数をコールバック関数 f_callback として定義しています。被積分関数を変数 amp、center、width でパラメータ化し、それらを Nag_User 構造体を使ってコールバック関数に渡します。フィット関数の内部で、NAG積分器d01smcを使って積分を実行します。
NAG関数を呼び出すのは、自分でルーチンを書き出すよりも効率的になるはずです。類似手法を使う事で、有限、無限、一次元、複数次元をフィット関数内で使用できるようになりました。NAG 直交 ページを読んで詳しく知りたいルーチンを選択してください。
パラメータの初期値または初期化コードを設定する
ユーザ定義のフィット関数なので、パラメータの初期値を指定する必要があります。非線形曲線フィットダイアログのパラメータタブで手動でセットすることができます。
関数をシミュレーションする
関数本体のコードを入力したら、コードビルダの「コンパイル」ボタンをクリックして、シンタックスにエラーがないかチェックすることができます。そして、「ダイアログに戻る」ボタンをクリックして、フィット関数オーガナイザダイアログボックスに戻ります。「保存」ボタンをクリックして、FDFファイル(関数定義ファイル)を生成します。
FDFファイルがあれば、「シミュレート」ボタンをクリックして、曲線のシミュレーションを行うことができ、これは初期値を求めるのに役立ちます。「simcurve」ダイアログで、適切なパラメータ値やX範囲を入力すると、「プレビュー」パネルに曲線がどのように表示されるのかが表示されます。
曲線をフィットする
曲線フィットを行う前に、関数のシミュレーションを行うことは大変役立ちます。積分の実行には、ある程度の時間がかかりますが、誤りがあると「フィット」ボタンをクリックした後、Originが反応しなくなる場合があります。そのため、フィット関数オーガナイザダイアログで、定義した関数を選択し、「シミュレート」ボタンをクリックします。すると、「simcurve」Xファンクションダイアログが開きます。推定される値を入力し、「適用」ボタンをクリックします。シミュレーションした曲線が、元のデータと近くなったら、フィットを行うことができます。
フィット関数をテストするには、
- OriginにSamples\Curve Fitting\Replicate Response Data.dat をインポートします。
- 次に、列Aのデータの対数スケールを使用します。そのために、列AのF(x) = 列ラベルに、列式Col(A) = log(Col(A)) を入力してEnterを押してデータを変換します。
- 列AとBを選択し、散布図を作成すると、形状はシグモイド型になっていることがわかります。
- NLFitダイアログを開くために、メニューから解析:フィット:非線形曲線フィットを選択します。
- 上述のセクションで定義したフィット関数を選択し、パラメータタブを開いて、すべてのパラメータを1で初期化し、フィットボタンをクリックします。
- 以下のような結果を得ることができます。
-
| |
値 |
標準誤差 |
| y0 |
-0.00806 |
0.18319 |
| A |
3.16479 |
0.39624 |
| xc |
-0.19393 |
0.10108 |
| w |
1.77252 |
0.33878 |
|