ノンパラメトリック検定概要

NonparametricStatisticsOverview

2つのサンプルのノンパラメトリック検定 複数サンプルのノンパラメトリック検定

概要

ノンパラメトリック検定はデータが正規分布するかわからない時や、正規分布に従わないと確認済みであるときに使用されます。

学習する項目

このチュートリアルでは、以下の項目について説明します。

• Originでのノンパラメトリック検定のイントロダクション
• 実際の様々な状況でノンパラメトリック検定を実行する方法
• ノンパラメトリック統計で相関係数を計算する方法

イントロダクション：Originでノンパラメトリック検定を行う

ノンパラメトリック検定は、正規性の仮定を必要としません。一般に、次のような状況で使用されます。

• 標本サイズが小さい
• カテゴリ/バイナリ/序数のデータ
• 正規分布と仮定できない場合

サンプル

1群の独立検定

1群のWilcoxon の符号順位検定は、特定の値に対して母集団の中央値が適切か否かを検定します。片側または両端の検定から選ぶことができます。Wilcoxon の符号順位検定の仮定は、「H0：中央値は仮定した中央値と等しい」に対して「H1：中央値は仮定した中央値と等しくない」になります。
この例では、製造店勤務の品質管理技術者が製品の重さの中央値（または、平均）が166と等しくなるか調べます。技術者は10個の製品をランダムに取り出し、重さを測りました。測定データは次のようになりました。
151.5 152.4 153.2 156.3 179.1 180.2 160.5 180.8 149.2 188.0
技術者は正規性検定このデータの分布が正規分布か否かを判断します。

1. 新しいワークシートを開き、上記データを列Aをに入力します。メニューから統計：記述統計：正規性検定...を選択して正規性検定ダイアログを開きます。
2. データ範囲として列A(X) を選択します。
   

   

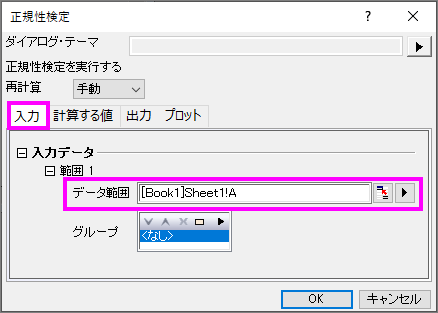
3. OKボタンをクリックし、結果を出力します。

   

結果によると、P値＝0.03814となっており、このデータは0.05レベルでは正規分布ではない、という事ができます。1群のWilcoxon符号付順位検定を実行するには

1. メニューから、統計：ノンパラメトリック検定：1群のWilcoxon符号付順位検定を選択してダイアログを開きます。
2. 列Aを入力としてセットします。
3. 検定の中央値として166をテキストボックスに入力します。

   

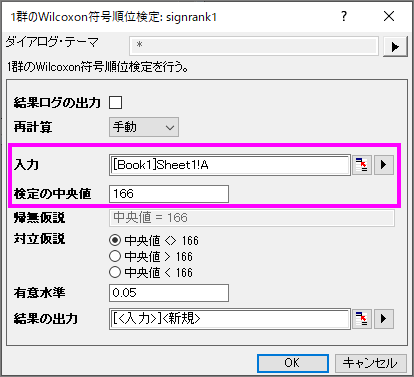
4. OKボタンをクリックし、結果を出力します。

   

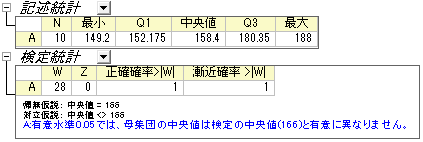
結果によると、帰無仮説を0.05レベルで棄却できないので、結果として中央値は166と等しいといえます。

2群の独立検定

Originは集団が独立システムとなっている時に使用できるノンパラメトリック統計検定として、マンホイットニー検定と2群のKolmogorov-Smirnov検定の2つを用意しています。

次の例題はマンホイットニー検定の実用的な例を示します。2種類のタイヤ（AとB）ですり減り具合（mg）の量を測定し、各タイヤに8つの実験が行われました。このデータはインデックス化され、abrasion_indexed.dat ファイルに保存されています。

1. \Samples\Statistics\ から abrasion_indexed.dat ファイルをインポートします。
2. メニューから統計：ノンパラメトリック検定：マンホイットニー検定と選択してダイアログを開きます。
3. 入力データフォームはインデックスのままにします。
4. 列Aをグループ範囲、列Bをデータ範囲と設定します。
5. 正確なP値チェックボックスにチェックを入れます。

   

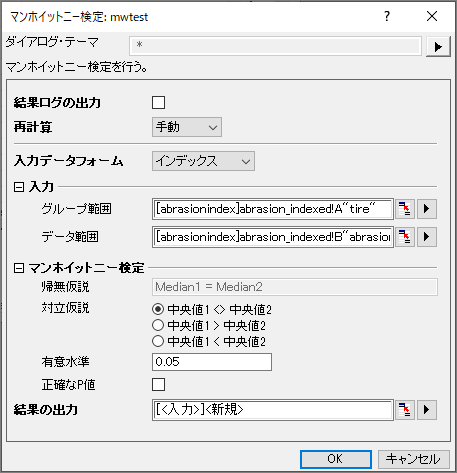
6. OKボタンをクリックするとMannWhitney1シートに結果が出力されます。

   

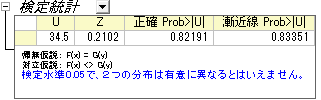
   • U： U統計は2群のランクから計算されます。2番目の群のスコアが1番目の群よりも大きかった回数を記録します。
   • Z： おおよその標準検定統計です。標本数が大きくなればなるほどより正確に予測できるようになります。
   • 正確なP値はダイアログ内で正確なP値を選択していないと確認できません。ただし、大きなサンプルの場合、CPU時間がかかります。
   • 漸近的P値: 漸近的P値はおおよその標準統計検定Zから計算されています。

相関に関するノンパラメトリック測定

相関係数は2つの変数間の関係性を見るのに使用されます。ノンパラメトリック統計でも、相関係数を計算することが可能です。

Originは相関係数を計算する2種類のノンパラメトリック手法を搭載しています。

• スピアマン： ピアソン相関係数の代替えとして良く利用されます。スピアマンの係数は、従属変数と独立変数の両方が序数、または、片方が序数でもう一方が連続変数である場合に利用できます。しかし、スピアマンの係数は両方の変数が連続数の場合でも使用できます。
• ケンドール： 序数の変数で利用され、各評価者間の同意地点見つけるために利用されます。

次のサンプルは、ノンパラメトリック状況の相関係数を計算する方法を示します。

1. \Samples\Statistics\ から abrasion_raw.dat ファイルをインポートします。
2. 列Aと列Bを選択します。メニューから統計：記述統計：相関係数と選択し、corrcoefダイアログを開きます。
3. スピアマンにチェックを入れ、ピアソンのチェックを外します。

   

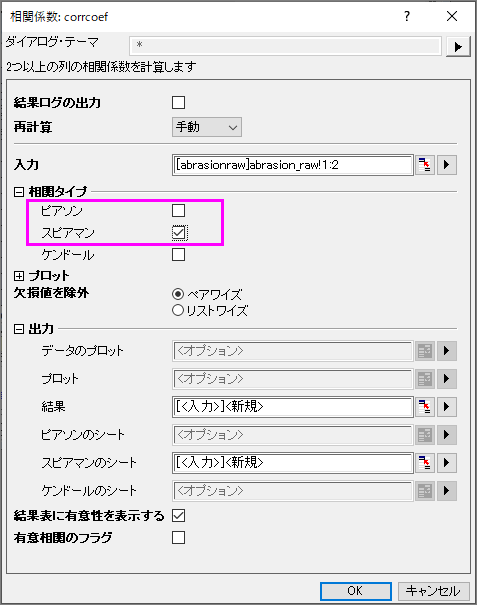
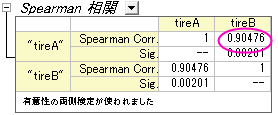
4. OKボタンをクリックし、CorrCoef1シートに結果を出力します。

Spearman相関の値から、AタイヤとBタイヤのすり減り具合には相関があるといえます。

対応のあるデータのWilcoxon符号順位検定

上記例で使用した、タイヤAとタイヤBの中央値を使用します。

1. \Samples\Statistics\ から abrasion_raw.dat ファイルをインポートします。
2. メニューから、統計：ノンパラメトリック検定：対応のあるデータのWilcoxon符号付順位検定を選択してダイアログを開きます。
3. 列Aを第1データ範囲、列Bを第2データ範囲と設定します。

   

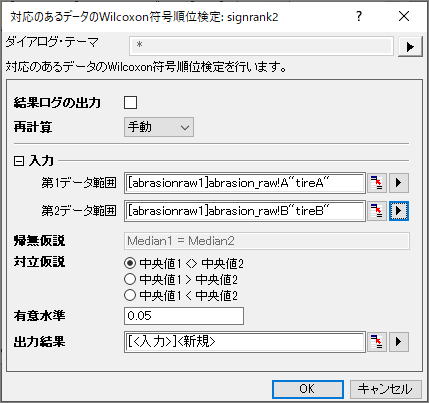
4. OKボタンをクリックし、結果を生成します。

   

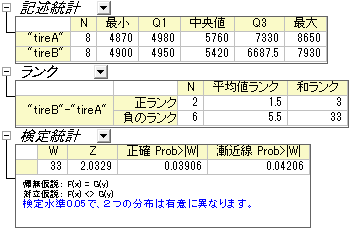
最終的に2つの中央値は有意に異なる、と結論付ける事ができます。一見して分かりますが、グループAの中央値の方がグループBより大きくなっています。

複数の独立標本検定

この例題では4種類の車の燃費が測定されました。各車に対して複数の実験が行われました。結果は以下の表にまとめられています。

これら4つの製造元で作られた車の燃費の等しさ、あるいは、一番効率的な車かを評価するのに、ノンパラメトリック検定の1つである、Kruskal-Wallis のANOVAを行います。

1. Originで新しいワークブックを作成し、そこにサンプルデータをコピーして貼り付けます。
2. メニューから統計：ノンパラメトリック検定：Kruskal-Wallis のANOVAと選択してkwanovaダイアログを開きます。
3. 入力データフォームとして、「素データ値」を選択します。
4. 入力の隣にある三角形のボタンをクリックし、コンテキストメニュー内にある全列を選びます。
   

   
   

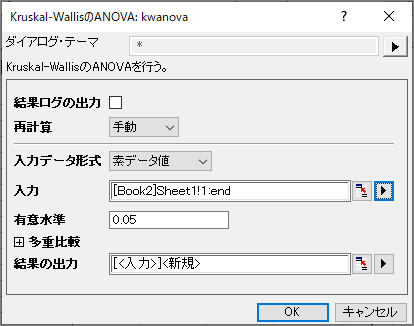
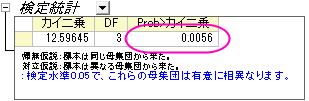
5. OKボタンをクリックすると結果を新しいワークシートKWANOVA1に表示します。

p値から、これらの4つの製造元の車の燃費は有意に異なるという事ができます。

複数の関連のある標本検定

眼科医がヘリウム・ネオンレーザー治療が子供に有効か調べています。6-10歳の子供たちのと11-16歳の子供たちの2群からのデータがあります。各データセットは5人の裸眼視力が3回の治療を通してどのように変わったのか記録しています。結果はeyesight.datに保存されています。

標本数が少ないのでノンパラメトリック検定を行います。次の手順に沿って操作してください。

1. \Samples\Statistics\ から eyesight.dat ファイルをインポートします。
2. メニューから統計：ノンパラメトリック検定：FriedmanのANOVAと選択してfriedmanダイアログを開きます。
3. 列Aをデータ範囲、列Cを因子範囲、列Dを従属する範囲と設定します。

   

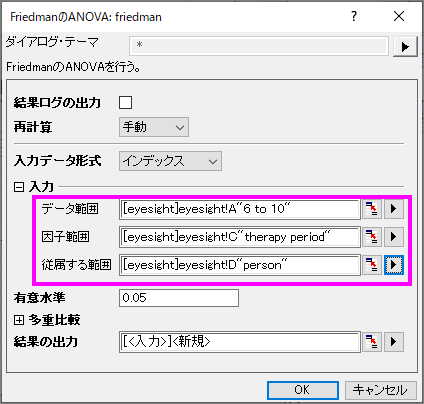
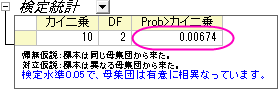
4. OKボタンをクリックし、結果を出力します。

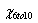のp値は0.0067379となっており、0.05よりも小さい値になっています。この2群は大きく異なる事が分かるので、治療は6-10歳の群には有効であるといえます。

同じように、列B をデータ範囲にして、他の入力設定はステップ3と同じようにします。

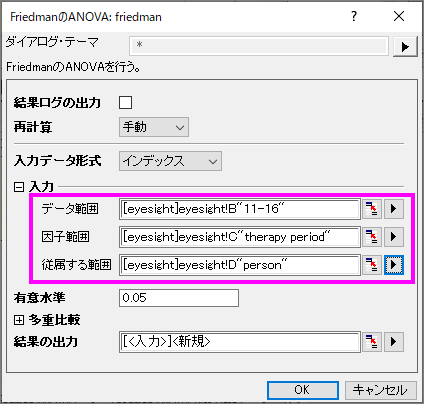
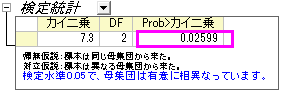
結果を確認すると、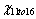のp値は0.02599となっており、0.05や0.10よりも小さくなっていることが分かります。つまり、11-16歳までの子供でも、3回の治療で視力が良くなっていると結論づける事ができます。

また、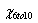>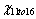という事が分かるので、ヘリウム・ネオンレーザー治療は6-10歳までの子供の方が良く効くといえます。まだ年齢が幼い子供たちがこの治療を行うと、視力が改善する可能性が高くなります。