2.75.2.2 Algorithm for Capability AnalysisAlgorithm-CA
Normal Capability Analysis
Standard Deviation Estimation
Within-subgroup and overall standard deviations are estimated for normal capability analysis.
- Within-subgroup Standard Deviation (
 ) )
- According to the subgroup size (bigger than 1, or equal to 1), estimating method is different.
- Subgroup Size > 1
- Average of Subgroup Ranges (Rbar)
-
 , where , where 
-
 : Number of subgroups : Number of subgroups
-
 : The range of the : The range of the  subgroup, subgroup, 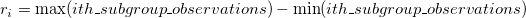
-
 : Number of observations in the : Number of observations in the  subgroup subgroup
-
 : Unbiasing constant, : Unbiasing constant, 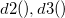
- Average of Subgroup Standard Deviations (Sbar)
- Unbiased
 , where , where 
- Not use unbiasing constant,
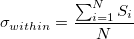
-
 : Number of subgroups : Number of subgroups
-
 : The standard deviation of the : The standard deviation of the  subgroup subgroup
-
 : Number of observations in the : Number of observations in the  subgroup subgroup
-
 : Unbiasing constant, : Unbiasing constant, 
- Pooled Standard Deviation
- Unbiased
 , where , where  , , 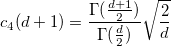
- Not use unbiasing constant,

-
 : Number of subgroups : Number of subgroups
-
 : Number of observations in the : Number of observations in the  subgroup subgroup
-
 : The : The  observation in the observation in the  subgroup subgroup
-
 : The Mean of the : The Mean of the  subgroup subgroup
-
 : Degrees of freedom for : Degrees of freedom for 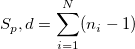
-
 : Unbiasing constant, : Unbiasing constant, 
-
 : Gamma function : Gamma function
- Subgroup Size = 1
- Average of Moving Range
-
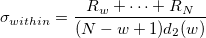
-
 : The number of all observations : The number of all observations
-
 : The number of observations used in the moving range : The number of observations used in the moving range
-
 : The : The  moving range. moving range.  , and , and  is the is the  observation observation
-
 : Unbiasing constant, : Unbiasing constant, 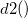
- Median of Moving Range
-
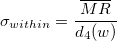
-
 : The number of all observations : The number of all observations
-
 : The number of observations used in the moving range : The number of observations used in the moving range
-
 : The : The  moving range. moving range.  , and , and  is the is the  observation observation
-
 : The median of the : The median of the 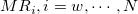
-
 : Unbiasing constant, : Unbiasing constant, 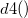
- Square Root of Mean Squared Successive Differences (MSSD)
- Unbiased
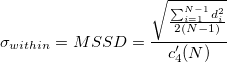
- Not use unbiasing constant,
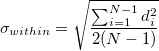
-
 : Number of observations : Number of observations
-
 : Succesive differences of observations : Succesive differences of observations
-
 : Unbiasing constant, : Unbiasing constant, 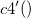
- Ovarall Standard Deviation (
 ) )
- Unbiased
 , where , where 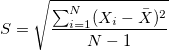
- Not use unbiasing constant,
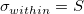
-
 : Number of all observations : Number of all observations
-
 : The : The  observation observation
-
 : The Mean of the all observations : The Mean of the all observations
-
 : Unbiasing constant, : Unbiasing constant, 
Potential Capability
- Cp
-
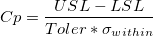
-
 : Upper and lower specification limits respectively : Upper and lower specification limits respectively
-
 : Multiplier of the sigma tolerance : Multiplier of the sigma tolerance
-
 : Within-subgroup standard deviation : Within-subgroup standard deviation
-
 Confidence Interval Bounds for Cp Confidence Interval Bounds for Cp
-
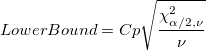
-
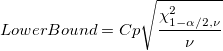
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Degrees of freedom : Degrees of freedom
-
 : :  percentile of chi-square distribution with percentile of chi-square distribution with  degrees of freedom degrees of freedom
-
 is calculated differently based on the method used for standard deviation. is calculated differently based on the method used for standard deviation.
- Average of Subgroup Ranges (Rbar):
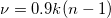
- Average of Subgroup Standard Deviations (Sbar):
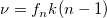
- Pooled standard deviation:
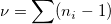
- Average of Moving Range or Median of Moving Range:

- Square Root of MSSD:

- where
 is the is the  subgroup size, subgroup size,  is number of subgroups, is number of subgroups,  is the length of the moving range, is the length of the moving range,  is the mean of subgroup size, is the mean of subgroup size,  , and , and  is calculated according to is calculated according to  as follows: as follows:
| n |
2 |
3 |
4 |
5 |
6,7 |
8,9 |
10-17 |
18-64 |
> 64
|
 |
0.88 |
0.92 |
0.94 |
0.95 |
0.96 |
0.97 |
0.98 |
0.99 |
1
|
- CPL
-
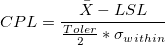
-
 : Process mean estimated from observations or historical value : Process mean estimated from observations or historical value
-
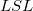 : Lower specification limit : Lower specification limit
-
 : Multiplier of the sigma tolerance : Multiplier of the sigma tolerance
-
 : Within-subgroup standard deviation : Within-subgroup standard deviation
- CPU
-
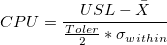
-
 : Process mean estimated from observations or historical value : Process mean estimated from observations or historical value
-
 : Upper specification limit : Upper specification limit
-
 : Multiplier of the sigma tolerance : Multiplier of the sigma tolerance
-
 : Within-subgroup standard deviation : Within-subgroup standard deviation
- Cpk
-

-
 Confidence Interval Bounds for Cpk Confidence Interval Bounds for Cpk
-
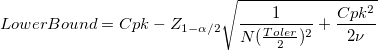
-

-
 : Total number of observations : Total number of observations
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Degrees of freedom, for details, please refer to : Degrees of freedom, for details, please refer to  Confidence Interval Bounds for Cp above Confidence Interval Bounds for Cp above
-
 : Multiplier of the sigma tolerance : Multiplier of the sigma tolerance
-
 : :  percentile from the standard normal distribution percentile from the standard normal distribution
- CCpk
-
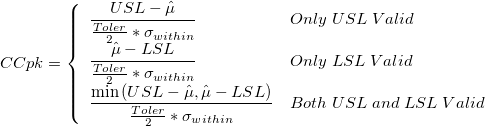
-
 : Estimated mean, : Estimated mean, 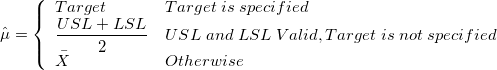
-
 : Upper and lower specification limits respectively : Upper and lower specification limits respectively
-
 : Multiplier of the sigma tolerance : Multiplier of the sigma tolerance
-
 : Within-subgroup standard deviation : Within-subgroup standard deviation
-
 : Mean of observations : Mean of observations
Overall Capability
- Pp
-
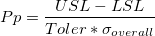
-
 : Upper and Lower specification limits respectively : Upper and Lower specification limits respectively
-
 : Multiplier of the sigma tolerance : Multiplier of the sigma tolerance
-
 : Overall standard deviation : Overall standard deviation
-
 Confidence Interval Bounds for Pp Confidence Interval Bounds for Pp
-
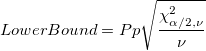
-
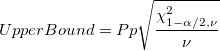
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Degrees of freedom, : Degrees of freedom, 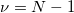
-
 : Number of observations : Number of observations
-
 : :  percentile of the chi-square distribution with percentile of the chi-square distribution with  degrees of freedom degrees of freedom
- PPL
-
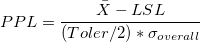
-
 : Process mean, can be historical value, or calculated from observations : Process mean, can be historical value, or calculated from observations
-
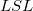 : Lower specification limit : Lower specification limit
-
 : Multiplier of the sigma tolerance : Multiplier of the sigma tolerance
-
 : Overall standard deviation : Overall standard deviation
- PPU
-
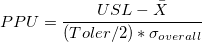
-
 : Process mean, can be historical value, or calculated from observations : Process mean, can be historical value, or calculated from observations
-
 : Upper specification limit : Upper specification limit
-
 : Multiplier of the sigma tolerance : Multiplier of the sigma tolerance
-
 : Overall standard deviation : Overall standard deviation
- Ppk
-
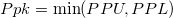
-
 Confidence Interval Bounds for Ppk Confidence Interval Bounds for Ppk
-
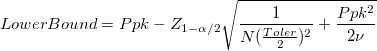
-
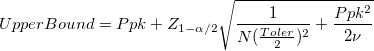
-
 : Number of observations : Number of observations
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Degrees of freedom, : Degrees of freedom, 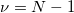
-
 : Multiplier of the sigma tolerance : Multiplier of the sigma tolerance
-
 : The : The  percentile from the standard normal distribution percentile from the standard normal distribution
- Cpm
- When
 is specified, it is able to calculate Cpm using is specified, it is able to calculate Cpm using  and and  . .
-

-
 : Upper and Lower specification limits respectively : Upper and Lower specification limits respectively
-
 : Target value : Target value
-
 : Multiplier of the sigma tolerance : Multiplier of the sigma tolerance
-
 : Midpoint between : Midpoint between  and and 
-
 : Number of observations in : Number of observations in  subgroup subgroup
-
 : The : The  observation in the observation in the  subgroup subgroup
-
 : Number of subgroups : Number of subgroups
-
 : Missing value : Missing value
-
 Confidence Interval Bounds for Cpm Confidence Interval Bounds for Cpm
- Two-Sided
-
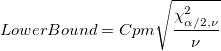
-

- One-Sided
-
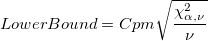
-
 : Degrees of freedom, : Degrees of freedom,  , where , where  , and , and  is the number of observations is the number of observations
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : :  quantile of the chi-square distribution with quantile of the chi-square distribution with  degrees of freedom degrees of freedom
Benchmark Zs for Potential Capability
- Z.LSL, Z.USL, and Z.Bench
-
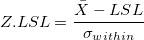
-
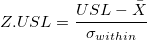
-
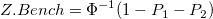
-
 : Process mean, estiimated from data, or historical mean : Process mean, estiimated from data, or historical mean
-
 : Lower and upper specification limits : Lower and upper specification limits
-
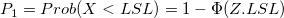
-
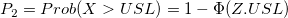
-
 : Cumulative distribution function of standard normal distribution : Cumulative distribution function of standard normal distribution
-
 : Inverse cumulative distribution function of standard normal distribution : Inverse cumulative distribution function of standard normal distribution
-
 : Within subgroups standard deviation : Within subgroups standard deviation
- Confidence Intervals for Z.Bench With Two Specification Limits
- Two-Sided
-
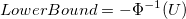
-
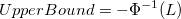
- where
-
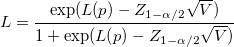
-
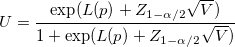
-
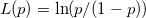
-

-

-
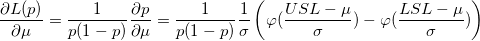
-
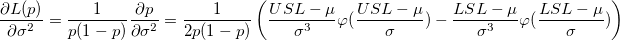
-
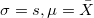
-
 : Total number of obsevations : Total number of obsevations
-
 : Tail probabilities outside of the specification limits : Tail probabilities outside of the specification limits
-
 : :  percential of standard normal distribution percential of standard normal distribution
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Process mean, estimated from data, or historical mean : Process mean, estimated from data, or historical mean
-
 : Lower and upper specification liimits : Lower and upper specification liimits
-
 : Within subgroups standard deviation : Within subgroups standard deviation
-
 : Degrees of freedom for : Degrees of freedom for 
-
 : Cumulative distribution function of standard normal distribution : Cumulative distribution function of standard normal distribution
-
 : Inverse cumulative distribution function of standard normal distribution : Inverse cumulative distribution function of standard normal distribution
-
 : Probability density function of standard normal distribution : Probability density function of standard normal distribution
- One-Sided
- Refer to the Two-Sided above, and change
 to to  in the definition of in the definition of  for for  . .
- Confidence Intervals for Z.Bench With One Specification Limit
- Lower Specification Limit and Two-Sided
-

-
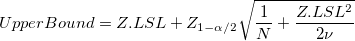
-
 : Total number of obsevations : Total number of obsevations
-
 : :  percential of standard normal distribution percential of standard normal distribution
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Degrees of freedom for standard deviation : Degrees of freedom for standard deviation
- Lower Specification Limit and One-Sided
-

-
 : Root of the equation: : Root of the equation: 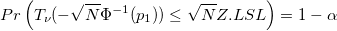
-
 : Total number of obsevations : Total number of obsevations
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Degrees of freedom for standard deviation : Degrees of freedom for standard deviation
-
 : Inverse cumulative distribution function of standard normal distribution : Inverse cumulative distribution function of standard normal distribution
-
 : Random variable that is distributed as non-central t distribution with : Random variable that is distributed as non-central t distribution with  degrees of freedom and non-centrality parameter degrees of freedom and non-centrality parameter 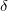
-
 : Cumulative distribution function of non-central t distribution : Cumulative distribution function of non-central t distribution
- Upper Specification Limit and Two-Sided
-
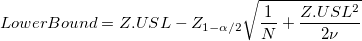
-
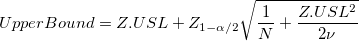
-
 : Total number of obsevations : Total number of obsevations
-
 : :  percential of standard normal distribution percential of standard normal distribution
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Degrees of freedom for standard deviation : Degrees of freedom for standard deviation
- Upper Specification Limit and One-Sided
-
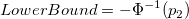
-
 : Root of the equation: : Root of the equation: 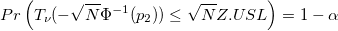
-
 : Total number of obsevations : Total number of obsevations
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Degrees of freedom for standard deviation : Degrees of freedom for standard deviation
-
 : Inverse cumulative distribution function of standard normal distribution : Inverse cumulative distribution function of standard normal distribution
-
 : Random variable that is distributed as non-central t distribution with : Random variable that is distributed as non-central t distribution with  degrees of freedom and non-centrality parameter degrees of freedom and non-centrality parameter 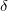
-
 : Cumulative distribution function of non-central t distribution : Cumulative distribution function of non-central t distribution
Benchmark Zs for Overall Capability
The calculation of benchmark Zs for overall capability is similar to potential capability, by replacing the  by by  . Please refer to Benchmark Zs for Potential Capability for more details. . Please refer to Benchmark Zs for Potential Capability for more details.
Expected Within Performance
- PPM < LSL and % < LSL
- The parts per million (PPM) less than the lower specification limit (PPM < LSL) and percentage less than the lower specification limit (% < LSL) are computed from the probability which is as follows:
-

-
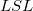 : Lower specification limit : Lower specification limit
-
 : Process mean, estimated from data, or historical mean : Process mean, estimated from data, or historical mean
-
 : Within subgroups standard deviation : Within subgroups standard deviation
-
 : Cumulative distribution function of standard normal distribution : Cumulative distribution function of standard normal distribution
- Then
 and and  are multiples of the above probability: are multiples of the above probability:
-
![[PPM\;<\;LSL] = 1000000\cdot P(X<LSL) [PPM\;<\;LSL] = 1000000\cdot P(X<LSL)](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-84564f37de1a39f24c6cb9dd5708ed26.png?v=0)
-
![[\%\;<\;LSL] = 100\cdot P(X<LSL) [\%\;<\;LSL] = 100\cdot P(X<LSL)](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-623573c0246d1799b35dee3cc2949122.png?v=0)
- Confidence Intervals for PPM < LSL and % < LSL
- Two-Sided
- Confidence intervals for
 are given by the following formulas are given by the following formulas
-

-
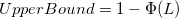
-
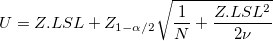
-

-
 : Cumulative distribution function of standard normal distribution : Cumulative distribution function of standard normal distribution
-
 : Number of observations : Number of observations
-
 : Alaph for confidence level : Alaph for confidence level
-
 : Degrees of freedom for standard deviation : Degrees of freedom for standard deviation
-
 : :  percentile of standard normal distribution percentile of standard normal distribution
- Then get
-
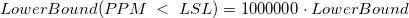
-
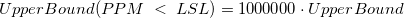
-

-
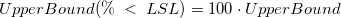
- One-Sided
-
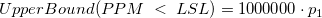
-
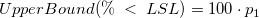
- where
 is the root of is the root of 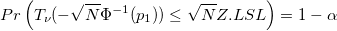
-
 : Total number of obsevations : Total number of obsevations
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Degrees of freedom for standard deviation : Degrees of freedom for standard deviation
-
 : Inverse cumulative distribution function of standard normal distribution : Inverse cumulative distribution function of standard normal distribution
-
 : Random variable that is distributed as non-central t distribution with : Random variable that is distributed as non-central t distribution with  degrees of freedom and non-centrality parameter degrees of freedom and non-centrality parameter 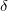
-
 : Cumulative distribution function of non-central t distribution : Cumulative distribution function of non-central t distribution
- PPM > USL and % > USL
- The parts per million (PPM) greater than the upper specification limit (PPM > USL) and percentage greater than the upper specification limit (% > USL) are computed from the probability which is as follows:
-
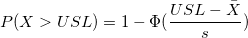
-
 : Upper specification limit : Upper specification limit
-
 : Process mean, estimated from data, or historical mean : Process mean, estimated from data, or historical mean
-
 : Within subgroups standard deviation : Within subgroups standard deviation
-
 : Cumulative distribution function of standard normal distribution : Cumulative distribution function of standard normal distribution
- Then
 and and  are multiples of the above probability: are multiples of the above probability:
-
![[PPM\;>\;USL] = 1000000\cdot P(X>USL) [PPM\;>\;USL] = 1000000\cdot P(X>USL)](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-b3f2b1ebff8af92438809bf160de3aa9.png?v=0)
-
![[\%\;>\;USL] = 100\cdot P(X>USL) [\%\;>\;USL] = 100\cdot P(X>USL)](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-71aa79fbde4f0dbc5a5ee7c84dd97c12.png?v=0)
- Confidence Intervals for PPM > USL and % > USL
- Two-Sided
- Confidence intervals for
 are given by the following formulas are given by the following formulas
-

-
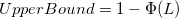
-
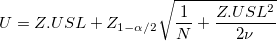
-
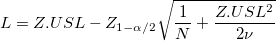
-
 : Cumulative distribution function of standard normal distribution : Cumulative distribution function of standard normal distribution
-
 : Number of observations : Number of observations
-
 : Alaph for confidence level : Alaph for confidence level
-
 : Degrees of freedom for standard deviation : Degrees of freedom for standard deviation
-
 : :  percentile of standard normal distribution percentile of standard normal distribution
- Then get
-
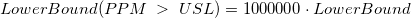
-
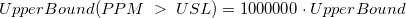
-
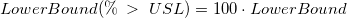
-
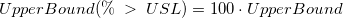
- One-Sided
-
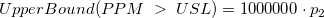
-
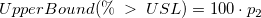
- where
 is the root of is the root of 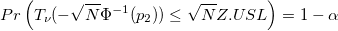
-
 : Total number of obsevations : Total number of obsevations
-
 : Alpha for the confidence level : Alpha for the confidence level
-
 : Degrees of freedom for standard deviation : Degrees of freedom for standard deviation
-
 : Inverse cumulative distribution function of standard normal distribution : Inverse cumulative distribution function of standard normal distribution
-
 : Random variable that is distributed as non-central t distribution with : Random variable that is distributed as non-central t distribution with  degrees of freedom and non-centrality parameter degrees of freedom and non-centrality parameter 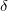
-
 : Cumulative distribution function of non-central t distribution : Cumulative distribution function of non-central t distribution
- PPM Total and % Total
- The parts per million that are outside the specification limits is calculated by:
-
![[PPM\;<\;LSL]+[PPM\;>\;USL] [PPM\;<\;LSL]+[PPM\;>\;USL]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-3ba7d313350351cbd5b69fb61c66a532.png?v=0) or or ![[\%\;<\;LSL]+[\%\;>\;USL] [\%\;<\;LSL]+[\%\;>\;USL]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-f0689c4d82d244e95315a317bfb79ba0.png?v=0)
- Confidence Intervals for PPM Total and % Total with Both Lower and Upper Specification Limits
- Two-Sided
-
 or or 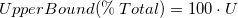
-
 or or 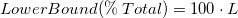
- The calculation of
 and and  can be referred to Benchmark Zs for Potential Capability for more details. can be referred to Benchmark Zs for Potential Capability for more details.
- One-Sided
-
 or or 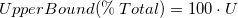
- Here
 is calculated using the same method as two-sided, but replacing is calculated using the same method as two-sided, but replacing  by by 
- Confidence Intervals for PPM Total and % Total with Only One Specification Limit (Lower Only or Upper Only)
- Lower Specification Limit Only
- Use the same calculation as the confidence interval for the PPM < LSL or % < LSL
- Upper Specification Limit Only
- Use the same calculation as the confidence interval for the PPM > USL or % > USL
Expected Overall Performance
- The calculation for expected overall performance is similar as the procedure for expected within performance, but by using overall standard deviation instead. For more details, please refer to Expected Within Performance.
Observed Performance
- PPM < LSL for Observed Performance
-
![[PPM\;<\;LSL(Observed)]=\frac{1000000\cdot(NumberOfObservations\;<\;LSL)}{N} [PPM\;<\;LSL(Observed)]=\frac{1000000\cdot(NumberOfObservations\;<\;LSL)}{N}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-0f147a368da30dba344b0e8da8192105.png?v=0) , where , where 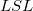 is lower specification limit, and is lower specification limit, and  is the total number of observations is the total number of observations
- PPM > USL for Observed Performance
-
![[PPM\;>\;USL(Observed)]=\frac{1000000\cdot(NumberOfObservations\;>\;USL)}{N} [PPM\;>\;USL(Observed)]=\frac{1000000\cdot(NumberOfObservations\;>\;USL)}{N}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-caecf3d1d03eac27b49c9339dea5e8a5.png?v=0) , where , where  is upper specification limit, and is upper specification limit, and  is the total number of observations is the total number of observations
- PPM Total for Observed Performance
-
![[PPM\;Total]=[PPM\;<\;LSL(Observed)]+[PPM\;>\;USL(Observed)] = \frac{1000000\cdot(NumberOfObservations\;<\;LSL)}{N}+\frac{1000000\cdot(NumberOfObservations\;>\;USL)}{N} [PPM\;Total]=[PPM\;<\;LSL(Observed)]+[PPM\;>\;USL(Observed)] = \frac{1000000\cdot(NumberOfObservations\;<\;LSL)}{N}+\frac{1000000\cdot(NumberOfObservations\;>\;USL)}{N}](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-4675815af9a334d3bee8286962f68903.png?v=0) , where , where 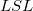 is lower specification limit, is lower specification limit,  is upper specification limit, and is upper specification limit, and  is the total number of observations is the total number of observations
Between/Within Capability Analysis
Standard Deviation Estimation
- Within Subgroup Standard Deviation (
 ) )
- Please refer to Standard Deivation Estimation for more details about pooled standard deviation, average of subgroup ranges, and average of subgroup standard deviation.
- Between Subgroup Standard Deviation (
 ) )
-

-
 is calculated by average of moving range, median of moving range or square root of mean squared successive differences. For more details, please refer to Standard Deivation Estimation. is calculated by average of moving range, median of moving range or square root of mean squared successive differences. For more details, please refer to Standard Deivation Estimation.
- Between/Within Standard Deviation (
 ) )
-

- Ovarall Standard Deviation (
 ) )
- Please refer to Overall Standard Deviation subsection in Standard Deivation Estimation.
Between/Within Capability
- Please refer to Potential Capability section for the calculations of Cp, CPL, CPU, Cpk, and CCpk. The difference is that the
 is replaced by is replaced by  . And, the calculation of . And, the calculation of  in the formula of Cp confidence interval is also different. Here, in the formula of Cp confidence interval is also different. Here,  is computed by: is computed by:
-

-
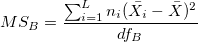
-
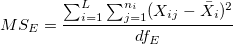
-
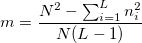
-
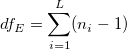
-
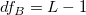
-
 : Total number of observations : Total number of observations
-
 : Number of subgroups : Number of subgroups
-
 : The : The  subgroup size subgroup size
-
 : Mean across all subgroups : Mean across all subgroups
-
 : Mean of the : Mean of the  subgroup subgroup
-
 : The : The  observation in the observation in the  subgroup subgroup
Overall Capability
- Please refer to Overall Capability section for more details.
Benchmark Zs for Between/Within Capability
- The calculation of benchmark Zs for between/within capability is similar to potential capability, by replacing the
 by by  . Please refer to Benchmark Zs for Potential Capability for more details. . Please refer to Benchmark Zs for Potential Capability for more details.
Benchmark Zs for Overall Capability
- The calculation of benchmark Zs for overall capability is similar to potential capability, by replacing the
 by by  . Please refer to Benchmark Zs for Potential Capability for more details. . Please refer to Benchmark Zs for Potential Capability for more details.
Expected Between/Within Performance
- The calculation of expected between/within performance is similar to expected within performance, by replacing the
 by by  . Please refer to Expected Within Performance for more details. And the following confidence intervals have different calculations: . Please refer to Expected Within Performance for more details. And the following confidence intervals have different calculations:
- Confidence Intervals for PPM < LSL and % < LSL
- One-Sided
-

-
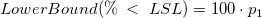
- Confidence Intervals for PPM > USL and % > USL
- One-Sided
-
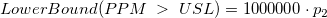
-
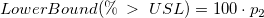
Expected Overall Performance
- The calculation for expected overall performance is similar as the procedure for expected within performance, but by using overall standard deviation instead. For more details, please refer to Expected Within Performance.
Observed Performance
- For more details, please refer to Observed Performance.
Non-normal Capability Analysis
Overall Capability
- Pp: Pp is computed by the parameters of the distribution used. Two methods are used for the Pp calculation, Z-Score method and ISO method.
- Z-Score Method
-
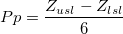
-
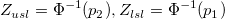
-
 : Inverse cumulative distribution function of standard normal distribution, : Inverse cumulative distribution function of standard normal distribution,  percentile of standard normal distribution percentile of standard normal distribution
-
 : Cumulative distribution function of the used distribution : Cumulative distribution function of the used distribution
-
 : Upper and Lower specification limits respectively : Upper and Lower specification limits respectively
- ISO Method
-
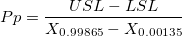
-
 : Upper and Lower specification limits respectively : Upper and Lower specification limits respectively
-
 : The : The  percentile of the used distribution percentile of the used distribution
- PPL
- Z-Score Method
-

-
 : Inverse cumulative distribution function of standard normal distribution, : Inverse cumulative distribution function of standard normal distribution,  percentile of standard normal distribution percentile of standard normal distribution
-
 : Cumulative distribution function of the used distribution : Cumulative distribution function of the used distribution
-
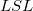 : Lower specification limit : Lower specification limit
- ISO Method
-
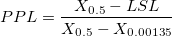
-
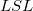 : Lower specification limit : Lower specification limit
-
 : The : The  percentile of the used distribution percentile of the used distribution
- PPU
- Z-Score Method
-
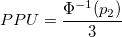
-
 : Inverse cumulative distribution function of standard normal distribution, : Inverse cumulative distribution function of standard normal distribution,  percentile of standard normal distribution percentile of standard normal distribution
-
 : Cumulative distribution function of the used distribution : Cumulative distribution function of the used distribution
-
 : Upper specification limit : Upper specification limit
- ISO Method
-
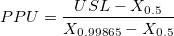
-
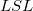 : Lower specification limit : Lower specification limit
-
 : The : The  percentile of the used distribution percentile of the used distribution
- Ppk
-
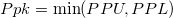
Overall Benchmark Zs for Non-normal Capability
- Z.LSL, Z.USL, and Z.Bench
-
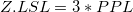
-

-
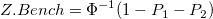
-
 : Cumulative distribution function of the used distribution, probability (X < LSL) based on the used nonnormal distribution : Cumulative distribution function of the used distribution, probability (X < LSL) based on the used nonnormal distribution
-
 : Cumulative distribution function of the used distribution, probability (X > USL) based on the used nonnormal distribution : Cumulative distribution function of the used distribution, probability (X > USL) based on the used nonnormal distribution
-
 : Cumulative distribution function of standard normal distribution : Cumulative distribution function of standard normal distribution
-
 : Inverse cumulative distribution function of standard normal distribution : Inverse cumulative distribution function of standard normal distribution
Expected Overall Performance
- PPM < LSL
- The parts per million (PPM) less than the lower specification limit (PPM < LSL) is computed from the probability which is as follows:
-
![[PPM\;<\;LSL]=1000000*F(LSL) [PPM\;<\;LSL]=1000000*F(LSL)](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-b7861569094c29fff193435a57705be7.png?v=0)
-
 : Parts per million : Parts per million
-
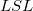 : Lower specification limit : Lower specification limit
-
 : Cumulative distribution function of the used nonnormal distribution : Cumulative distribution function of the used nonnormal distribution
- PPM > USL
- The parts per million (PPM) greater than the upper specification limit (PPM > USL) is computed from the probability which is as follows:
-
![[PPM\;>\;USL]=1000000*(1-F(USL)) [PPM\;>\;USL]=1000000*(1-F(USL))](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-6fadde38604b3c02630726109c255cff.png?v=0)
-
 : Parts per million : Parts per million
-
 : Upper specification limit : Upper specification limit
-
 : Cumulative distribution function of the used nonnormal distribution : Cumulative distribution function of the used nonnormal distribution
- PPM Total
-
![[PPM\;Total] = [PPM\;<\;LSL] + [PPM\;>\;USL] [PPM\;Total] = [PPM\;<\;LSL] + [PPM\;>\;USL]](//d2mvzyuse3lwjc.cloudfront.net/doc/en/App/images/Algorithm_CA/math-68b360dfa1b595e43a76d66886d0d62e.png?v=0)
Observed Performance
- For more details, please refer to Observed Performance.
Distribution
- For more details, please refer to Distributions.
Binomial Capability Analysis
Average P
-
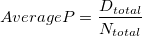
-
 : Sum of all defectives : Sum of all defectives
-
 : Sum of all sample sizes : Sum of all sample sizes
Average P 95% Confidence Interval
-
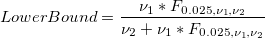
-
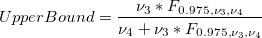
-

-

-
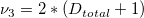
-
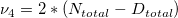
-
 : Sum of all defectives : Sum of all defectives
-
 : Sum of all sample sizes : Sum of all sample sizes
-
 : Inverse F cumulative distribution function : Inverse F cumulative distribution function
%Defective
-
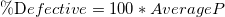
%Defective 95% Confidence Interval
-
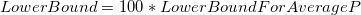
-
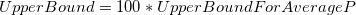
PPM Defective
-
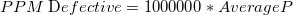
PPM Defective 95% Confidence Interval
-
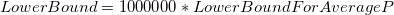
-
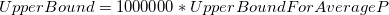
Process Z
-
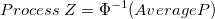
-
 : Inverse comulative distribution function of standard normal distribution : Inverse comulative distribution function of standard normal distribution
Process Z 95% Confidence Interval
-

-
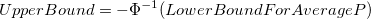
-
 : Inverse cumulative distribution function of standard normal distribution : Inverse cumulative distribution function of standard normal distribution
Poisson Capability Analysis
Mean Defective
-

-
 : Sum of all defectives : Sum of all defectives
-
 : Number of samples : Number of samples
Mean Defective 95% Confidence Interval
-
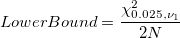
-
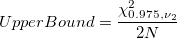
-

-

-
 : Sum of all defectives : Sum of all defectives
-
 : Number of samples : Number of samples
-
 : Inverse Chi Square cumulative distribution function : Inverse Chi Square cumulative distribution function
Mean DPU
-
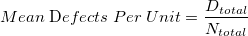
-
 : Sum of all defectives : Sum of all defectives
-
 : Sum of all sample sizes : Sum of all sample sizes
Mean DPU 95% Confidence Interval
-
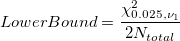
-
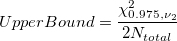
-

-

-
 : Sum of all defectives : Sum of all defectives
-
 : Sum of all sample sizes : Sum of all sample sizes
-
 : Inverse Chi Square cumulative distribution function : Inverse Chi Square cumulative distribution function
Minimum DPU
- The minimum defects per unit among all samples.
Maximum DPU
- The maximum defects per unit among all samples.
|