ROC-Kurve

ROC-Curve

Zusammenfassung

Die Analyse mit der ROC-Kurve (Receiver Operating Characteristic) wird hauptsächlich für diagnostische Studien in der klinischen Chemie, Pharmakologie und Physiologie verwendet. Sie wird weithin als die Standardmethode zum Beschreiben und Vergleichen der Genauigkeit von Diagnosetests eingesetzt.

Bitte lesen Sie in der Origin-Hilfe weitere Einzelheiten zur Verwendung der ROC-Kurve.

Was Sie lernen werden

Dieses Tutorial zeigt Ihnen, wie Sie:

• eine Analyse mit der ROC-Kurve durchführen.
• die Ergebnisse der Analyse interpretieren.

Schritte

In diesem Beispiel wird eine Untersuchung durchgeführt, um herauszufinden, ob das Serumnatrium einen Beitrag zur Diagnose des Fiebers Rocky Mountain Spotted Fever (RMSF) leisten kann.

Die Daten stammen von Personen mit und ohne RMSF. Die Natriumkonzentration wird für jede Person mit Hilfe von 2 Screening-Techniken gemessen. Die Analyse mit der ROC-Kurve wird für die Daten mit beiden Methoden durchgeführt. Die Beziehung zwischen Serumnatrium und RMSF wird geprüft. Außerdem ist es leichter zu beurteilen, welche Diagnostemethode besser geeignet ist.

1. Öffnen Sie ein leeres Arbeitsblatt. Wählen Sie Hilfe: Ordner öffnen: Sample-Ordner ... im Menü, um den Ordner "Samples" zu öffnen. Öffnen Sie in diesem Ordner den Unterordner Statistics. Dort befindet sich die Datei sodium.dat. Ziehen Sie diese Datei per Drag&Drop in das leere Arbeitsblatt, um sie zu importieren.
2. Wählen Sie Statistik: ROC-Kurve, um den Dialog der ROC-Kurve zu öffnen.
3. Wählen Sie im Zweig Eingabedaten die Spalten B(Method1) und C(Method2) für Daten und die Spalte A(Sickness) für Zustand.
4. Wählen Sie RMSF als Positiven Zustandwertaus und aktivieren Sie die Option Positiv vs. Niedrig für die Testrichtung im Zweig Steuerung Berechnung.
5. Aktivieren Sie Optimaler Schnittpunkt im Zweig ROC-Kurve.
6. Übernehmen Sie alle anderen Standardeinstellungen und klicken Sie auf die Schaltfläche OK, um die Analyse durchzuführen.

   

Ergebnisinterpretation: Wechseln Sie zum Arbeitsblatt ROC Curve1, in dem die Analysergebnisse festgehalten sind.

In dieser Tabelle können ersehen, dass die Asymptotische Wahrscheinlichkeit von beiden Methoden viel kleiner ist als 0,05. Daher können wir schlussfolgern, dass beide Methoden effektiv sind.

Je näher der Bereich ind er ROC-Analyse an 1,0 liegt, desto besser ist der Test. Im Gegensatz dazu gilt, je näher der Bereich an 0,5 liegt, desto schlechter ist der Test. In dieser Analyse sind die Bereiche von Methode 1 und Methode 2 0,88862 bzw. 0,79407. Beide Ergebnisse sind damit viel größer als 0,5. Der Bereich von Methode 1 liegt jedoch näher an 1,0. Daher können wir schlussfolgern, dass Methode 1 besser geeignet ist als Methode 2.

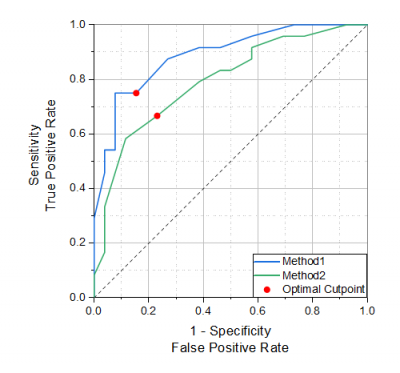
Zusätzlich können wir die Form der ROC-Kurve untersuchen, die ebenfalls in dem Berichtsblatt enthalten ist. Da Methode 1 scheinbar über eine größere Sensitivität verfügt als Methode 2, können wir schlussfolgern, dass Methode 1 wahrscheinlich etwas besser ist als Methode 2.