| Hinweis: Alle der folgenden Funktionen sind nur in Origin 8 SR6 oder neueren Versionen verfügbar! |
| Name | Brief Description |
|---|---|
| Between(str$, str1$, str2$)$ | Extrahiert Zeichenkette oder Zeichen zwischen str1$ und str2$ in str$. Beispiele:
|
| Char(number)$ | Nimmt eine ganze Zahl 1-255, gibt das ASCII-Zeichen aus. Beispiele:
|
| Code(str$) | Nimmt eine Zeichenkette, gibt den ASCII-Code für das erste Zeichen aus.. Beispiele:
|
| Compare(str1$, str2$ [,Case]) | Nimmt zwei Zeichenketten, gibt 1 (identisch) oder 0 (nicht identisch) aus. Die Option Case steuert die Groß-/Kleinschreibung: 1 = wahr (Standard), 0 = falsch. Beispiele:
|
| CompareNoCase(str$, str2$) | Nimmt zwei Zeichenketten, gibt 0 aus (identisch), -1 (str$ ist kleiner als str2$ in alphabetischer Reihenfolge) oder 1(str$ ist größer als str2$). Beispiele:
|
| EnvVar(variableName$) | Nimmt eine Zeichenkette, gibt den Wert der Zeichenkette gespeichert in der entsprechenden Windows-Umgebungsvariablen aus. Wenn diese Zeichenkette keine gültige Variablenzeichenkette der Windows-Umgebung ist, werden Fehlende ausgegeben. Beispiele:
|
| Exact(str1$, str2$) | Nimmt zwei Zeichenketten, gibt 1 aus (identisch, einschließlich Groß-/Kleinschreibung) oder 0 (nicht identisch). Beispiele:
|
| Find(within$,find$[,StartPos]) | Sucht within$ für find$, gibt die Position vom ersten Zeichen in within$ (gefunden) oder -1 (nicht gefunden) aus. Die Option StartPos steuert die erste Anfangssuchposition (Standard = 1). Groß- und Kleinschreibung beachten Keine Platzhalter. Beispiele:
|
| FindOneOf(within$,find$) | Sucht find$ für das erste in within$ gefundene Zeichen. Wenn es gefunden wird, wird der 1-Basis-Index des ersten gefundenen Zeichens ausgegeben. Groß- und Kleinschreibung beachten Keine Platzhalter. Beispiele:
|
| GetAt(str$,index) | Gibt ein einzelnes Zeichen festgelegt durch Index in str$ aus. Beispiele:
|
| GetFileExt(strFile$)$ | Die Dateierweiterung erhalten Sie aus dem vollständigen Pfad strFile$. Beispiele:
|
| GetFileName(strFile$,bRemoveExt)$ | Den Dateinamen erhalten Sie (ohne Erweiterung, falls bRemoveExt = 1) aus dem vollständigen Pfad strFile$. Beispiele:
|
| GetFilePath(strFile$)$ | Den Pfad erhalten Sie aus dem vollständigen Pfad strFile$. Beispiele:
|
| GetLength(str$) | Die Länge erhalten Sie aus einer str$. Beispiele:
|
| GetToken(str$,n,chDelimiter)$ | Gibt das n-te Token aus, wo ein Token durch einen chDelimiter getrennt wird. Beispiele:
|
| IsEmpty(str$) | Ähnlich der Funktion ISBLANK von MS Excel. Verwendet, um zu bestimmen, ob eine Arbeitsblattzelle leer ist oder nicht. Das Argument str kann eine Zellenadresse oder eine Spalte mit Werten sein. Beispiel:
|
| IsFile(str$) | Testen Sie, ob str ein gültiger vollständiger Pfaddateiname ist. Beispiel:
|
| IsFormula(str$) | Bestimmt, ob eine Arbeitsblattszelle eine Zellenformel enthält oder nicht. Beispiel:
|
| IsPath(str$) | Testen Sie, ob str ein gültiger Pfaddateiname ist. Beispiel:
|
| Left(str$, n)$ | Nimmt eine Zeichenkette str$, gibt die am weitesten links stehenden n Zeichen aus. Beispiele:
|
| Len(str$) | Nimmt eine Zeichenkette str$, gibt die Anzahl der Zeichen aus. Beispiele:
|
| Lower(str$)$ | Nimmt eine Zeichenkette str$ und konvertiert sie in Kleinbuchstaben. . Beispiele:
|
| MakeCSV(str$[, quote, output_delim, input_delim$])$ | Nimmt eine begrenzte Zeichenkette und konvertiert sie in CSV. Die Option quote umschließt die Ausgabe: 0 (Standard) = keine Anführungszeichen, 1 = einzelne Anführungszeichen, 2 = doppelte Anführungszeichen. Option output_delim: 0 = Komma, 1 = Semikolon. Die Option input_delim$ legt die begrenzte Quellzeichenkette fest (bei Weißraum nicht notwendig). Beispiele:
|
| Match(within$,find$[,Case]) (2015 SR0) |
Diese Funktion vergleicht die Zeichenkette find$ mit einer anderen Zeichenkette within$, um zu sehen, ob ihre Inhalte miteinander übereinstimmen. Es wird 1 (wahr, Übereinstimmung) oder 0 (falsch, keien Übereinstimmung) ausgegeben. Beachten Sie, dass die Platzuhalter "*" und "?" in der Zeichenkettenvariable find$ unterstützt werden. Optional können Sie die Groß-/Kleinschreibung verwenden. Die Option Case steuert die Groß-/Kleinschreibung: 0 (Standard) = falsch, 1 = wahr. Beispiele:
|
| MatchBegin(within$,find$[,StartPos,Case]) | Sucht die Zeichenkette within$, gibt eine ganze Zahl entsprechend der Anfangsposition von find$ oder -1 (nicht gefunden) aus. Unterstützt die Platzhalter "*"' und "?". Die Option StartPos legt die Position der Zeichen fest, bei der die Suche begonnen wird: 1 (Standard) = Suche ab dem ersten Zeichen. Die Option Case steuert die Groß-/Kleinschreibung: 0 (Standard) = falsch, 1 = wahr. Beispiele:
|
| MatchEnd(within$, find$[, StartPos, Case]) | Sucht die Zeichenkette within$, gibt eine ganze Zahl entsprechend der Endposition von find$ oder -1 (nicht gefunden) aus. Unterstützt die Platzhalter "*" und "?". Die Option StartPos legt die Position der Zeichen fest, bei der die Suche begonnen wird: 1 (Standard) = Suche ab dem ersten Zeichen. Die Option Case steuert die Groß-/Kleinschreibung: 0 (Standard) = falsch, 1 = wahr. Beispiele:
|
| Mid(str$, StartPos [, n])$ | Nimmt eine Zeichenkette str$, gibt n Zeichen ab StartPos oder, falls n nicht festgelegt ist, alles ab StartPos aus. Beispiele:
|
| NumberValue(str$ [, Decimal$, Group$]) | Nimmt eine Zeichenkette oder einen Vektor der Zeichenketten und gibt eine Zahl aus. Die Option Dezimal wird verwendet, um das Dezimaltrennzeichen der Zeichenkette zu interpretieren. Die Option Group wird verwendet, um das Gruppentrennzeichen zu interpretieren. Zeichenketten und Optionen werden in Anführungszeichen eingeschlossen. Beispiele:
|
| Replace(within$, StartPos, n, replace$)$ | Ersetzt n Zeichen in within$, angefangen bei StartPos, mit der Zeichenkette replace$. Die Zeichenkette replace$ kann sich in der Länge von n unterscheiden. Beispiele:
|
| Right(str$, n)$ | Nimmt eine Zeichenkette str$, gibt die am weitesten rechts stehenden n Zeichen aus. Beispiele:
|
| Search(within$, find$[, StartPos]) | Gibt die Position der Zeichenkette find$ innerhalb der Zeichenkette within$ oder, falls diese nicht gefunden wird, -1 aus. Groß- und Kleinschreibung nicht beachten. Keine Platzhalter. Die Option StartPos steuert, wo die Suche gestartet wird (Standard = 1). Beispiele:
|
| SpanExcluding(source$, strEx$) | Extrahiert und gibt alle Zeichen vor dem ersten Auftreten eines Zeichens von strEx aus; berücksichtigt Groß- und Kleinschreibung. Beispiele:
|
| SpanIncluding(source$, strIn$) | Extrahiert Zeichen aus der Zeichenkette source, angefangen mit dem ersten Zeichen, das sich in dem Zeichensatz befindet, der mit strIn identifiziert wird; berücksichtigt Groß- und Kleinschreibung. Beispiele:
|
| Substitute(within$,sub$,find$ [, n])$ | Sucht die Zeichenkette within$ für die Zeichenkette find$, ersetzt sie mit sub$. Die Option ersetzt nur die n-te gefundene Instanz. Beispiele:
|
| Text(d[,fmt$])$ (9,1 SR0) |
Konvertiert ein Double in eine Zeichenkette. Die Option fmt$ formatiert die Ausgabe und nimmt diese Werte; falls nicht anders festgelegt, werden die Formateinstellungen der Spalte verwendet. Verwendet eine leere Zeichenkette "", um @SD Stellen zu verwenden. Verwendet "*", um die globalen Einstellungen von Origin zu verwenden. Beispiele:
|
| Token(str$,iToken[, iDelimiter])$ | Nimmt die Zeichenkette str$, gibt die Unterzeichenkette aus, die dem Index iToken entspricht. Die Option iDelimiter ist ein ASCII-Wert des Trennzeichens: 0 (Standard) = jeglicher Weißraum; 32 = einzelnes Leerzeichen; 124 = "|". Die meisten Symbolzeichen wie "_" (ASCII 95), "|"(ASCII 124) können direkt als iDelimiter verwendet werden. Beispiele:
Hinweis: Einige Symbolzeichen können nicht direkt von iDelimiter verwendet werden, aber ihre ASCII-Werte gelten immer. |
| Trim(str$[, n])$ | Nimmt die Zeichenkette str$ und entfernt Leerzeichen. Der Parameter n steuert, wie Leerzeichen entfernt werden: 0 (Standard) = Anfang + Ende, 1 = alle entfernen. Beispiele:
|
| Upper(str$)$ | Nimmt die Zeichenkette str$, gibt sie in Großbuchstaben aus. Beispiele:
|
| Value(str$) | Nimmt die Zeichenkette str$, gibt sie als Double aus. Beispiele:
|
Hinweis: Die Verwendung von "$", wenn Sie mit Zeichenketten arbeiten, kann verwirrend sein:

aa$=col(b)[1]; aa$=; // returns col(b)[1]
aa$=col(b)[1]$; aa$=; // returns Buick
aa$=upper(col(b)[1]$); aa$=; // returns upper(col(b)[1]$)
aa$=upper(col(b)[1]$)$; aa$=; // returns BUICK
| Name | Brief Description |
|---|---|
| abs(x) | Gibt den absoluten Wert von x aus. Beispiel:
|
| ceil(x[, sig]) (2019 SR0) |
Gibt einen Wert aus, indem der gegebene Wert x weg von 0 und an das Mehrfache von sig am nächsten an d angepasst wird. Beispiel:
|
| Combina(n,k) (2019 SR0) |
Bei gegebenen n Elementen wird die Anzahl der Kombinationen von k Elementen mit Wiederholungen ausgegeben. Beispiel:
|
| Combine(n1,n2) | Bei gegebenen n1 Elementen wird die Anzahl der Kombinationen von n2 Elementen ausgegeben. Beispiel:
|
| Distance(px1, py1, px2, py2) | Nimmt die XY-Koordinaten von zwei Punkten, gibt die kürzeste Distanz aus. Beispiele:
|
| Distance3D(px1, py1, pz1, px2, py2, pz2) | Nimmt die XYZ-Koordinaten von zwei Punkten, gibt die kürzeste 3D-Distanz aus. Beispiele:
|
| exp(x) | Gibt e hoch x aus. Hinweis: x > 667 gibt fehlenden wert aus. Beispiele:
|
| expm1(x) | Gibt den Wert von exp(x)-1 genau für die kleinen Werte von x aus. Beispiele:
|
| fact(n) | Gibt den Faktor einer nicht-negativen Ganzzahl aus. Hinweis: n > 170 gibt den fehlenden Wert aus; siehe die Funktion Log_gamma. Beispiele:
|
| factdouble(n) | Gibt die doppelte Fakultät einer nicht-negativen ganzen Zahl aus. Wenn n = ungerade, dann ist die Sequenz 1*3*5...(n-2)*n; wenn n = gerade, dann ist die Sequenz 2*4*6...(n-2)*n; wenn n = 0, wird auf 1 ausgewertet. Wenn n > 299, wird der fehlende Wert ausgegeben. Beispiele:
|
| floor(x[, sig]) (2019 SR0) |
Gibt einen Wert aus, indem der gegebene Wert x in Richtung 0 und an das Mehrfache der Signifikanz von x angepasst wird. Beispiel:
|
| gcd(n1, n2[, ...]) (2019 SR0) |
Gibt den größten gemeinsamen Teiler einer Gruppe von gegebenen ganzen Zahlen n1, n2, n3 etc. aus. Beispiel:
|
| frac(x) | Gibt den Bruchanteil eines Double aus. Beispiel:
|
| HaversineDistance(lon1,lat1,lon2,lat2,r[,degree]) (2017 SR0) |
Nimmt die Längen- und Höhengrade von zwei Punkten in einer Kugel mit dem Radius r, gibt die Distanzen des Großkreises zwischen ihnen aus. Die Option degree bestimmt, ob Grad oder Radiant als die Einheit für Längen- und Höhengrad verwendet wird (Standard ist Grad). Beispiel:
|
| int(x) | Nimmt ein doppeltes x und gibt die gekürzte ganze Zahl aus. Beispiele:
|
| ln(x) | Gibt den natürlichen Logarithmus von x aus. |
| ln1p(x) | Gibt den naturürlichen Logarithmus von x aus, wenn x sehr nah bei 1 liegt. |
| log(x) | Gibt den Logarithmus zur Basis 10 von x aus. |
| mod(n, m) | Gibt den ganzzahligen Modulo der ganzen Zahl n geteilt durch die ganze Zahl m aus (Quotient wird auf 0 gerundet). Beispiele:
|
| mod2(n,m) | Gibt den ganzzahligen Modulo der ganzen Zahl n geteilt durch die ganze Zahl m aus (Quotient wird gen minus Unendlichkeit gerundet). Quotient von  , verwendet, um den Modulo zu berechnen, wird Richtung , verwendet, um den Modulo zu berechnen, wird Richtung  gerundet. Wenn die Eingabe(n) negativ sind, kann sich die Ausgabe von mod unterscheiden (Der Quotient von gerundet. Wenn die Eingabe(n) negativ sind, kann sich die Ausgabe von mod unterscheiden (Der Quotient von  wird auf 0 gerundet). Beispiele: wird auf 0 gerundet). Beispiele:
|
| nint(x) | Nimmt ein doppeltes x und rundet auf/ab zur nächsten ganzen Zahl. Die Funktion nint(x) gibt das gleiche Ergebnis aus wie round(x, 0). |
| permut(n, k) (2019 SR0) |
Gibt die Anzahl der Permutationen für festgelegte k Elemente von einem gegebenen Satz von n Elementen aus. Beispiele:
|
| prec(x, n) | Nimmt einen Wert oder einen Datensatz, gibt diesen mit n signifikanten Ziffern aus. Beispiele:
|
| product(vd) | Multipliziert alle Zahlen aus vd und gibt das Produkt aus. Beispiele:
|
| rmod(x, y) | Gibt den realen Modulo des doppelten x geteilt durch das doppelte y aus (Quotient wird auf 0 gerundet). Quotient von  wird auf wird auf 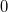 gerundet. Beispiele: gerundet. Beispiele:
|
| rmod2(x, y) | Gibt den realen Modulo des doppelten x geteilt durch das doppelte y aus (Quotient wird gen minus Unendlichkeit gerundet). Quotient von  wird auf wird auf  gerundet. Beispiele: gerundet. Beispiele:
|
| round(x, n) | Nimmt einen Wert oder Datensatz, gibt den Wert oder Datensatz mit n Dezimalstellen aus. Hinweis: Origin 9.1 führte einen neuen Rundungsalgorithmus ein. Die Systemvariable @RNA wechselt zwischen alten und neuen Methoden (altes Verhalten ist @RNA=0; neues Verhalten ist @RNA=1 (Standard)). Beispiele:
|
| sign(x) | Nimmt eine reale Zahl x und gibt das Vorzeichen aus. Wenn x > 0, wird 1 ausgegeben; wenn x < 0, wird -1 ausgegeben; wenn x = 0, wird 0 ausgegeben. |
| sqrt(x) | Nimmt ein doppeltes x und gibt die Quadratwurzel aus.. |
| Derivative(vd[,n]) | Nimmt einen Vektor vd, gibt die Ableitung der Datenliste aus. Es wird keine Glättung durchgeführt. Die Option n ist die Ableitungsordnung (Standard = 1). |
| DerivativeXY(vx, vy [, n]) | Nimmt zwei Vektoren vx und vy, gibt die Ableitung der Kurve aus. Die Option n ist die Ableitungsordnung (Standard = 1). |
| Integral(integrand,lowerlimit,upperlimit[, arg1, arg2, ...]) | Führt einen Dimensionsintegrationswert durch und gibt den Integralwert aus.
|
| Integrate(vd) | Die Fläche unter einer Kurve wird integriert. Verwendet die Trapezregel. |
| IntegrateXY(vx, vy) | Die Fläche unter der Kurve wird integriert (vx, vy). Der Vektor vx enthält X-Koordinaten der Kurve; vy enthält Y-Koordinaten. |
| Interp(x,vX,vY[,method,bound,smooth,extrap]) (2015 SR0) |
Nimmt die x-Koordinaten vx und y-Koordinaten vy und interpoliert/extrapoliert eine y-Koordinate bei einer gegebenen Koordinate x. Die Option method = 0 (linear, Standard), 1 (kubische Spline), 2 (kubische B-Spline), 3 (Akima-Spline). Wenn method = 1, kann bound gleich 0 (natürlich) oder 1 (Not-a-Knot) sein. When method = 2, ist smooth = nicht negativer Wert für Glättung. Die Option extrap kann angewendet werden, wenn die X-Werte sich außerhalb der Referenzbereichs befinden: 0 (Standard) = Y mit Hilfe von zwei Punkten extrapolieren; 1 = alle Y als fehlende Werte festlegen; 2 = den Y-Wert des nächsten eingegebenen X verwenden. |
| permutationa(n, k) (2019 SR0) |
Gibt die Anzahl der Permutationen (mit Wiederholungen) für festgelegte k Elemente von einem gegebenen Satz von n Elementen aus. Beispiele:
|
| Name | Brief Description |
|---|---|
| beta(a, b) | Beta-Funktion mit Parametern a und b.
|
| incbeta(x, a, b) | Unvollständige Beta-Funktion mit Parametern x, a, b.
|
| incf(x, m, n) | Die unvollständige Funktion F-table Der Parameter x ist die obere Grenze der Integration; der Parameter m stellt die Freiheitsgrade der Zählervarianz dar; der Parameter n stellt die Freiheitsgrade der Nennervarianz dar. |
| incgamma(a,x) | Berechnet die unvollständige Gamma-Funktion bei x mit dem Parameter a.
wobei |
| inverf(x) | Berechnet die inverse Fehlerfunktion bei x. |
| j0(x) | Bessel-Funktion 0-ter Ordnung. |
| j1(x) | Bessel-Funktion 1. Ordnung. |
| jn(x, n) | Bessel-Funktion der Ordnung n.
wobei |
| y0(x) | Bessel-Funktion 0-ter Ordnung und 2. Art. |
| y1(x) | Bessel-Funktion 1. Ordnung und 2. Art. |
| yn(x, n) | Bessel-Funktion n-te Ordnung und 2. Art.
wobei
|
| Hinweis: Winkeleinheiten (Radiant, Grad, Gon) hängen von der Eigenschaft system.math.angularunits ab (auch festzulegen in Einstellungen: Optionen: Zahlenformat). |
| Name | Brief Description |
|---|---|
| acos(x) | Gibt den Arkuskosinus von x aus. Wenn x < -1 oder x > 1, wird der fehlende Wert ("--") ausgegeben. |
| acosh(x) | Gibt den inversen hyperbolischen Kosinus von x aus. Wenn x < 1, wird der fehlende Wert ("--") ausgegeben. |
| acot(x) | Gibt den Arkustangens von x aus. Die Eingabe von x kann jeder Wert sein. Die Werte werden im ersten oder zweiten Quadranten ausgegeben. |
| acoth(x) | Gibt den inversen hyperbolischen Kotangens von |x| > 1 aus. |
| acsc(x) | Gibt den Arkuskosekans von | x aus. Wenn |x| < 1, wird der fehlende Wert ("--") ausgegeben. Die Werte werden im ersten oder vierten Quadranten ausgegeben. |
| acsch(x) | Gibt den inversen hyperbolischen Cosekans von x aus. Wenn x = 0 oder x > ~3E153, wird der fehlende Wert ("--") ausgegeben. |
| angle(x, y) | Gibt den Winkel (Radiant), gemessen zwischen der positiven X-Achse und der Linie, die den Punkt (x,y) und den Ursprung (0,0) verbindet, aus. |
| Angleint1(px1, py1, px2, py2 [, unit, direction]) | Nimmt zwei Paare von XY-Koordinaten, gibt den Winkel zwischen der durch zwei Punkte definierten Linie und der X-Achse aus. Die Option unit = 0 Radiant (Standard) oder 1 (Grad); die Option direction: 0 (Standard) beschränkt den ausgegebenen Winkelwert auf den ersten (+x,+y) und den vierten (+x,-y) Quadranten; oder 1 gibt die Werte von 0–2pi Radiant oder 0–360 Grad aus. Beispiele:
|
| Angleint2(px1, py1, px2, py2, px3, py3, px4, py4 [, unit, direction]) | Gibt den Winkel zwischen zwei Linien aus, eine mit den Endpunkten (px1, py1) und (px2, py2), die andere mit den Endpunkten (px3, py3) und (px4, py4). Wenn die Option unit = 0 (Standard), wird der Radiant ausgegeben; wenn unit = 1, wird Grad ausgegeben. Die Option direction legt die Richtung der Ausgabewerts fest. Wenn die Option direction = 0 (Standard), beschränkt sich der ausgegebene Winkelwert auf den ersten (+x,+y) und den vierten (+x,-y) Quadranten; wenn direction = 1, werden Werte von 0–2pi Radiant oder 0–360 Grad ausgegeben. Beispiele:
|
| asec(x) | Gibt den Arkussekans von x aus. Wenn |x| < 1, wird der fehlende Wert ("--") ausgegeben. Die Werte werden im ersten oder zweiten Quadranten ausgegeben. |
| asech(x) | Gibt den inversen hyperbolischen Sekans von x aus. 0 < x ≤ 1. Andere Werte von x geben einen fehlenden Wert ("--") aus. |
| asin(x) | Gibt den Arkussinus von x aus. -1 ≤ x ≤ 1. Andere Werte von x geben einen fehlenden Wert ("--") aus. |
| asinh(x) | Gibt den inversen hyperbolischen Sinus von x (jede reale Zahl) aus. |
| atan(x) | Gibt den Arkustangens von x (jede reale Zahl) aus. |
| atan2(y,x) | Nimmt die Koordinaten x,y (Doubles), gibt den Winkel zwischen der positiven X-Achse und dem Punkt (x,y) aus. Eine Variation der Funktion atan(x). Gibt den Wert zwischen -π und π aus. Winkel ist (+) für Winkel gegen den Uhrzeigersinn (y > 0) und (-) für Winkel im Uhrzeigersinn (y < 0). |
| atanh(x) | Gibt den inversen hyperbolischen Tangens von x aus. -1 < x < 1. Andere Werte von x geben einen fehlenden Wert ("--") aus. |
| cos(x) | Gibt den Kosinus von x aus. |
| cosh(x) | Gibt den hyperbolischen Kosinus von x aus. |
| cot(x) | Gibt den Kotangens von x aus. |
| coth(x) | Gibt den hyperbolischen Kotangens von x aus. Der Wert x ist eine beliebige Zahl, die nicht Null ist. Beachten Sie, dass die Zahlen des absoluten Werts > 710 (ca.) einen fehlenden Wert ("--") ausgeben. |
| csc(x) | Gibt den Cosekans von x aus. Wenn x = 0, wird der fehlende Wert ("--") ausgegeben. |
| csch(x) | Gibt den hyperbolischen Kosekans von x aus. Der Wert x ist eine beliebige Zahl, die nicht Null ist. Hinweis: Wenn x > 710 (ca.), wird ein fehlender Wert ("--") ausgegeben. |
| Degrees(angle) | Nimmt angle in Radiant und gibt Grad aus.. |
| Radians(angle) | Nimmt angle in Grad und gibt Radiant aus.. |
| secant(x) | Gibt den Sekans von x aus. Hinweis: Verwechseln Sie diese Funktion nicht mit der Funktion sec(), die den Sekundenwert eines Datums ausgibt. |
| sech(x) | Gibt den hyperbolischen Sekans von x aus. Beachten Sie, dass die Zahlen des absoluten Werts > 710 (ca.) einen fehlenden Wert ("--") ausgeben. |
| sin(x) | Gibt den Sinus von x aus. |
| sinh(x) | Gibt den hyperbolischen Sinus von x aus. |
| tan(x) | Gibt den Tangens von x aus. |
| tanh(x) | Gibt den hyperbolischen Tangens von x aus. |
Hinweis: Ab Origin 2019 gibt es drei Datums-/Zeit-Systeme in Origin. Das Standardsystem bleibt das langjährige angepasste Julianische Datumssystem wie unter Daten und Zeiten in Origin erklärt. Die Beispiele in der Tabelle unten setzen das Standardsystem für Datum und Zeit voraus. Wenn Sie "Julianischer Datumswert" sehen, bezieht sich dies auf Origins angepassten Datumswert. Diese folgenden Funktionen sollten mit alternativen Systemen arbeiten ...
date2str(today(), "MM/dd/yyyy")$ = 09/27/2018 // default date-time system date2str(today(), "MM/dd/yyyy")$ = 09/27/2018 // "2018" system, @DSP=2018
...aber bedenken Sie, dass numerische Werte, die einem gegebenen Kalenderdatum entsprechen, sich zwischen den Systemen unterscheiden:
date(9/27/2018) = 2458388 // default date-time system date(9/27/2018) = 269 // "2018" system, @DSP=2018
Informationen zu Origins alternativen Datum-Zeit-Optionen finden Sie unter Alternative Datums-/Zeit-Systeme in Origin.
| Name | Brief Description |
|---|---|
| AddDay(vv) (2021) |
Nimmt einen Zeitvektor vv und gibt Daten mit einem hinzugefügten Tag aus, wenn die Stunden nach 24 beendet werden. Beispiele:
|
| Date(MM/dd/yyHH:mm:ss.##[,format$]) | Nimmt die Datums-/Zeit-Zeichenkette und gibt den Wert des Julianischen Datums aus. Wenn format$ nicht festgelegt ist, wird die Zeichenkette mit Hilfe des Systemformats für Kurzdaten interpretiert. Kann die Werte 1 = Standard (MM/dd/yyyy) , 2 (dd/MM/yyyy) oder 3 (yyyy/MM/dd) nehmen, um das Format für den Datumsteil des ersten Arguments zu steuern, ohne die Zeichenkette format$ festzulegen. Beispiele:
|
| Date(yy,MM,dd) | Nimmt doppelte yy als Jahr, mm als Monat, dd als Tag und gibt das Julianische Datum aus. Beispiele:
|
| Date2str(d,format$)$ | Nimmt ein Julianisches Datum und gibt eine Datumszeichenkette aus. Beispiele:
|
| DatePart(datepart$, d [, n]) (2016 SR1) |
Nimmt ein Julianisches Datum (doppelt) d und gibt einen Teil des Datums, der durch datepart$ festgelegt wurde, als Double aus. Die Option n legt den Anfang der Woche für datepart$ = w or ww fest. Beispiele:
|
| Day(d[,n]) | Nimmt einen Julianischen Datumswert, gibt die Tageszahl aus. Wenn Option n = 1, wird 1 bis 31 (Monat) ausgegeben; wenn n = 2, wird 1 bis 366 (Jahr) ausgegeben. Beispiele:
|
| Hour(d) | Nimmt einen Julianischen Datumswert und gibt die Stunde als eine ganze Zahl aus. Gibt 0 bis 23 (0 = 12:00 A.M., 23 = 11:00 P.M.) aus. Beispiele:
|
| Minute(d) | Nimmt ein Julianisches Datum, gibt die Minuten als eine ganze Zahl aus (0 bis 59). Beispiele:
|
| Month(d) | Nimmt ein Julianisches Datum, gibt den Monat als eine ganze Zahl aus (0 bis 12). Beispiele:
|
| MonthName(d[,n])$ | Nimmt ein Julianisches Datum, gibt den Monatsnamen aus. Monatsformat festgelegt durch die Option n: 1 = einzelnes Zeichen; 3 (Standard) = 3 Zeichen; 0 = voller Monatsname; -1 = 3 englisches Zeichen, unabhängig von den Spracheinstellungen. Beispiele:
|
| Now() | Gibt den aktuellen Wert für Datum/Zeit als einen Julianischen Datumswert aus. Beispiele:
|
| Quarter(d) | Nimmt einen Julianischen Datumswert, gibt ein Jahresquartal aus. Beispiele:
|
| Second(d[,n]) | Nimmt ein Julianisches Datum oder eine reale Zahl, gibt die Sekunden als einen realen Wert im Bereich 0 bis 59,9999 aus. Die Option n = 0 zeigt mehr als 3 Dezimalstellen an, die Präzision der Julianischen Datumswerte ist jedoch auf 0,0001 Sekunden beschränkt, wenn auf die vierte Dezimalstelle gerundet wurde. Beispiele:
|
| Time(HH,mm,ss) und Time(HH:mm:ss[,Format$]) | Nimmt entweder HH,mm,ss oder eine benutzerdefinierte Datum-Zeit-Zeichenkette (HH:mm:ss = Standard) und gibt das Julianische Datum aus. Optional legt das Argument Format$ das benutzerdefinierte Zeichenkettenformat fest. Beispiele:
|
| Time2str(d,format$)$ | Nimmt ein Julianisches Datum, gibt eine Zeichenkette der Zeit eines festgelegten Formats aus. Beispiele:
|
| Today() | Gibt das aktuelle Datum als einen Julianischen Datumswert aus. |
| UnixTime(d1[, d2, n]) (2021) |
Konvertieren Sie Unix-Zeitstempelwerte in Julianische Datumswerte. Falls der optionale Parameter n = 0 (Standard), wird d1 (Unix-Zeitstempel) in ein Julianisches Datum verwandelt; falls n = 1, wird d1 (Julianisches Datum) in einen Unix-Zeitstempel verwandelt. Der optionale Parameter d2 ist der Versatz für die Zeitzone. Beachten Sie, dass Sie beim Konvertieren eines Julianischen Datums in einen Unix-Zeitstempel beide optionale Parameter festlegen müssen (falls kein Versatz, d2 = 0). Einheit der Unix-Zeitstempel = Sekunden. Beispiele:
|
| WeekDay(d[,n]) | Nimmt ein Julianisches Datum, gibt den Wochentag aus. Die Option n legt Wochenanfang und -ende fest: 0 (Standard) = Sonntag (0-6), 1 = Sonntag (1-7), 2 = Montag (0-6) oder 3 = Montag (1-7). Beispiele:
|
| WeekDayName(d[,n1,n2])$ | Nimmt ein Julianisches Datum (einschließlich Zeit) oder eine durch n2 definierte Zahl, gibt den Wochentag aus. Die Option n1 steuert die Länge der Ausgabezeichenkette: -1 = 3 Char Cap; 0 = voller Name, 1. Cap; 1 = 1 Char Cap; 3 (Standard)= 3 Char, 1. Cap. Die Option n2 steuert die Werte für Wochenanfang und -ende: 0 = 0(Sun) - 6(Sat); 1 = 1(Sun) - 7 (Sat); 2 = 0(Mon) - 6(Sun); 3(default) = 1(Mon) - 7(Sat). Beispiele:
|
| WeekNum(d[,n]) | Nimmt ein Julianisches Datum, gibt die Kalenderwochenzahl des Jahres (1 bis 53). Die Option zum Festlegen des Wochenanfangs (Sonntag vs. Montag). Beispiele:
|
| Year(d) | Nimmt einen Julianischen Datum, gibt das Jahr als eine ganze Zahl aus (0100-9999). Beispiele:
|
| YearName(d[,n])$ | Nimmt ein Julianisches Datum, gibt das Jahr als Zeichenkette aus. Die Form der Zeichenkette wird durch die Option n festgelegt: 0 = 2 Stellen, 1 (Standard) = 2 Stellen mit einem vorangestelltem Apostroph oder 2 = 4 Stellen. Beispiele:
|
| Name | Brief Description |
|---|---|
| if(con,val_true[,val_false])[$] (2019 SR0) |
Wertet den Bedingungsausdruck con aus und gibt val_true aus, wenn der Vergleich TRUE ist, val_false, wenn er FALSE ist. Beispiel
|
| ifs(con1,val1[,con2,val2,]...[,con40,val40])[$] (2019 SR0) |
Wertet mehrere Bedingungen conn aus und gibt das entsprechende d/str der ersten Bedingung TRUE aus. Beispiel
|
| ifna(val,val_na)[$] (2019 SR0) |
Berechnet den gegebenen Wert val und gibt die festgelegte Zeichenkette/numerischer Wert val_na aus, wenn das Ergebnis fehlt. Ansonsten wird die Zeichenkettenanzeige des Ergebnisses von val/numerischer Wert val ausgegeben. Beispiel
|
| switch(expression,val1,res1[,val2,res2]...[,val39,res39][,default])[$] (2019 SR0) |
Wertet expression mit einem Satz Werte val aus, und falls es einen übereinstimmenden Wert valn gibt, gibt es das entsprechende resn aus. Beispiel
|
| Name | Brief Description |
|---|---|
| fftamp(cx [,side]) (2015 SR1) |
Nimmt einen komplexen Vektor cx (normalweise das komplexe FFT-Ergebnis), gibt die Amplitude aus. Die Option side definiert das Ausgabespektrum (1 = einseitig, 2 = zweiseitig und Verschiebung). Beispiele:
|
| fftc(cx) (2015 SR1) |
Nimmt einen Vektor cx, gibt das komplexe FFT-Ergebnis aus. Beachten Sie, dass der Datentyp der Ausgabespalte vorher auf komplex (16) gesetzt werden muss. Beispiele:
|
| fftfreq(time, n[, side , shift]) (2015 SR1) |
Nimmt das Abtastintervall time und die Signalgröße n, gibt die Frequenzen für das FFT-Ergebnis aus. Die Option side definiert das Ausgabespektrum (1 = einseitig, 2 = zweiseitig), Verschiebung und ob die Verschiebung zu beiden Seiten stattfindet. ( 0 = keine Verschiebung, 1 = Verschiebung). Beispiele:
|
| fftmag(cx [,side]) (2015 SR1) |
Nimmt einen komplexen Vektor cx (normalerweise das komplexe FFT-Ergebnis), gibt den Betrag aus. Die Option side definiert das Ausgabespektrum (1 = einseitig, 2 = zweiseitig und Verschiebung). Beispiele:
|
| fftphase(cx[, side, unwrap, unit]) (2015 SR1) |
Nimmt einen komplexen Vektor cx (normalerweise das komplexe FFT-Ergebnis), gibt die Phase aus. Die Option side definiert das Ausgabespektrum (1 = einseitig, 2 = zweiseitig und Verschiebung), unwrap defininiert, ob der Phasenwinkel nicht umhüllt werden soll (0 = umhüllen, 1 = nicht umhüllen), unit definiert die Einheit (0 = Radiant, 1 = Grad). Beispiele:
|
| fftshift(cx) (2015 SR1) |
Nimmt einen komplexen Vektor cx (normalerweise das komplexe FFT-Ergebnis oder die Frequenz), gibt den verschobenen Vektor aus. Beachten Sie, dass der Datentyp der Ausgabespalte vorher auf komplex (16) gesetzt werden muss. Beispiele:
|
| ifftshift(cx) (2015 SR1) |
Nimmt einen komplexen Vektor cx (normalerweise das verschobene FFT-Ergebnis), gibt einen nicht verschobenen Vektor aus. Beachten Sie, dass der Datentyp der Ausgabespalte vorher auf komplex (16) gesetzt werden muss. Beispiele:
|
| invfft(cx) (2015 SR1) |
Nimmt einen komplexen Vektor cx (normalerweise das komplexe FFT-Ergebnis), gibt das inverse FFT-Ergebnis aus. Beachten Sie, dass der Datentyp der Ausgabespalte vorher auf komplex (16) gesetzt werden muss. Beispiele:
|
| windata(type, n) (2015 SR1) |
Nimmt ganze Zahlen von type (Fenstertyp) und n (Fenstergröße), gibt das Fenstersignal als einen Vektor der Größe n aus. Beispiel:
|
| Name | Brief Description |
|---|---|
| Count(vd[,n]) | Nimmt einen Vektor vd, gibt die Anzahl der Elemente aus. Die Option n legt das Element fest: 0 (Standard) = all; 1 = numerisch; 2 = fehlend; 3 = Fehlende ausschließen Beispiel:
|
| Max(vd) | Nimmt einen Vektor vd, gibt den maximalen Wert aus. Beispiel:
|
| Mean(vd) | Nimmt einen Vektor vd, gibt den Durchschnitt aus. Beispiel:
Hinweis: Wenn Sie den Durchschnitt von mehreren Datensätzen pro Zeile berechnen wollen, können Sie die Syntax
Siehe weitere Informationen unter die Funktion sum(vd). |
| Median(vd[,method]) | Nimmt einen Vektor vd, gibt den Median aus. Die Option method legt die Interpolationsmethode fest: 0 (Standard) = empirische Verteilung mit Durchschnitt; 1 = nächster Nachbar; 2 = empirische Verteilung; 3 = gewichteter Durchschnitt rechts; 4 = gewichteter Durchschnitt links; 5 = Tukey Hinges). Beispiel:
|
| Min(vd) | Nimmt einen Vektor vd, gibt den minimalen Wert aus. |
| Ss(vd [,ref]) | Nimmt einen Vektor vd, gibt die Summe der Quadrat aus. Die Summe der Quadrate wird berechnet, nachdem ein Referenzwert ref von jedem Wert in vd subtrahiert wurde. Die Option ref setzt den Mittelwert von vd als Standard, ref kann aber eine Konstante, ein Datensatz oder eine Funktion sein. Beispiel:
|
| StdDev(vd) | Nimmt einen Vektor vd, gibt die Standardabweichung der Stichprobe aus. Beispiel:
|
| StdDevP(vd) | Nimmt einen Vektor vd, gibt die Standardabweichung der Grundgesamtheit aus. Beispiel:
|
| Sem(vd) (2020b) |
Nimmt einen Vektor vd, gibt den Standardfehler aus. Beispiel:
|
| Total(vd) | Nimmt einen Vektor vd, gibt die Summe der Elemente aus. Beispiel:
|
| averageif(vd, con$) | Nimmt einen Vektor vd und ein konditionales con$ und gibt das Mittel der Werte aus, um con$ zu erfüllen. Beispiel:
|
| Countif(vd,con$) | Nimmt einen Vektor vd, gibt die Anzahl der Werte aus, die die Bedingung con$ erfüllen. Die Bedingung con$ sollte durch doppelte Anführungszeichen (" ") umschlossen werden.
|
| Maxifs(vd,con$) | Nimmt einen Vektor vd, gibt die maximalen Werte aus, die die Bedingung con erfüllen. Beispiel
|
| Minifs(vd,con$) | Nimmt einen Vektor vd, gibt die minimalen Werte aus, die die Bedingung con erfüllen. Beispiel
|
| sumif(vd,con$) | Nimmt einen Vektor vd, gibt die Summe der Werte aus, die die Bedingung con$ erfüllen. |
| Name | Brief Description |
|---|---|
| Correl(vx, vy) | Nimmt die Datensätze vx und vy, gibt den Korrelationskoeffizienten aus. Beispiel:
|
| cov(vx, vy[, avex, avey]) | Nimmt die Datensätze vx und vy und die jeweiligen Mittelwerte avex und avey, gibt die Kovarianz aus. Beispiel:
|
| Forecast(x,vx,vy) | Nimmt die x-Koordinaten vx und y-Koordinaten vy und führt eine lineare Regression aus, um eine y-Koordinate bei einer gegebenen Koordinate x zu berechnen oder zu prognostizieren. |
| Intercept(vx,vy) | Nimmt zwei Vektoren vx (unabhängig) und vy (abhängig) und gibt den Schnittpunkt der Y-Achse mit der linearen Regression aus. |
| mae(vobs,vpred) (2023b) |
Nimmt zwei Vektoren, vobs(Beobachtung) und vpred (Prognose), und gibt den mittleren absoluten Fehler aus. |
| mbe(vobs,vpred) (2023b) |
Nimmt zwei Vektoren, vobs(Beobachtung) und vpred (Prognose), und gibt den mittleren Bias-Fehler aus. |
| rms(vd) | Nimmt einen Vektor vd, gibt den quadratischen Mittelwert aus. |
| rmse(vobs,vpred) (2023b) |
Nimmt zwei Vektoren, vobs(Beobachtung) und vpred (Prognose), und gibt den Fehler der Quadratwurzel des Mittelwerts aus. |
| Slope(vx,vy) | Nimmt zwei Vektoren, vx (unabhängig) und vy (abhängig), und gibt der Steigung mit der linearen Regression aus. |
| ave(vd, size[, stats]) | Nimmt einen Vektor vd, gibt einen Bereich der Durchschnitte von jeder Gruppe der Größe aus. stats bietet einen Option zum Ausgeben weiterer Statistikeigenschaften abgesehen vom Durchschnitt. Wenn Elemente von vd kein gerades Mehrfaches von size sind, dann stellt der ausgegebene Durchschnitt nur mod (vdSize,size) Elemente dar. Beispiel:
|
| diff(vd[,n]) | Nimmt einen Vektor vd, gibt einen Bereich der Differenzen zwischen nebeneinander liegenden Elementen aus. Das erste Element im ausgegebenen Bereich ist vd(i+1)-vdi und so weiter. Gibt N-1, N oder N+1 Elemente aus, abhängig von dem Wert des optionalen Parameters n:
|
| sum(vd) | Die Funktion sum() hat zwei Modi: Im "Spalten"modus kann sie einen Vektor vd der einzelnen Spalte nehmen und einen Vektor ausgeben, der die Werte der kumulativen Summe (von 1 bis i, i=1,2,...,N) beinhaltet. Sein i+1-tes Element ist die Summer der ersten i Elemente. Das letzte Element des ausgegebenen Bereichs ist die Summe aller Elemente im Datensatz. Beispiel:
|
| Confidence(alpha, std, size[, dist]) | Nimmt das Signifikanzniveau alpha, die Standardabweichung der Grundgesamtheit std und den Stichprobenumfang size, gibt das Konfidenzintervall für den Mittelwert der Grundgesamtheit mit Hilfe der Verteilung dist aus. Beispiel:
|
| Geomean(vd) | Nimmt einen Vektor vd und gibt den geometrischen Mittelwert aus.
|
| Geosd(vd) | Nimmt einen Vektor vd und gibt die geometrische Standardabweichung aus.
|
| Harmean(vd) | Nimmt einen Vektor vd und gibt den harmonischen Mittelwert aus.
|
| histogram(vd, inc, min, max) | Nimmt einen Vektor vd, die Klassenbreite = inc, vd min sowie vd max und erzeugt die Dateneinteilungen. Datenpunkte, die am oberen Rand der Klasse liegen, werden der nächst höheren Klasse zugeordnet. |
| Kurt(vd) | Nimmt einen Vektor vd, gibt die Kurtosis aus. Beispiel:
|
| lcl(vd[, level]) | Nimmt einen Vektor vd, gibt die untere Konfidenzgrenze bei level aus. Beispiel:
|
| Mad(vd) | Nimmt einen Vektor vd, gibt die absolute Abweichung des Mittelwerts aus. Beispiel:
|
| Mode(vd) | Nimmt einen Vektor vd und gibt die am häufigsten auftretende Zahl in vd aus. Beispiel:
|
| Modes(vd) | Nimmt einen Vektor vd und gibt einen Vektor der am häufigsten auftretenden Zahl(en) in vd aus. Beispiel:
|
| Percentile(vx, vy) | Nimmt einen Vektor vx, gibt die Perzentilwerte bei jedem Prozentwert, festgelegt in vy, aus. Beispiel:
|
| QCD2(n) | Nimmt einen Stichprobenumfang n, gibt den Faktor der Qualitätskontrolle D2 aus. Beispiel:
|
| QCD3(n) | Nimmt einen Stichprobenumfang n, gibt den Faktor der Qualitätskontrolle D3 aus. Faktor D3 ist die untere 3-Sigma-Kontrollgrenze im X-quer-R-Diagramm. Beispiel:
|
| QCD4(n) | Nimmt einen Stichprobenumfang n, gibt den Faktor der Qualitätskontrolle D4 aus. Faktor D4 ist die obere 3-Sigma-Kontrollgrenze im X-quer-R-Diagramm. Beispiel:
|
| Skew(vd) | Nimmt einen Vektor vd, gibt die Schiefe (Verteilungssymmetrie) aus. Beispiel:
|
| ucl(vd[, level]) | Nimmt einen Vektor vd, gibt die obere Konfidenzgrenze bei level (Standard ist 0,95) aus. Beispiel:
|
| Emovavg(vd,n[,method]) | Nimmt einen Vektor vd und eine ganze Zahl n = Zeitraum, gibt einen Vektor des exponentiellen gleitenden Durchschnitts aus. Die Option method legt fest, wo Berechnungen beginnen: 0 (Standard) = ab Punkt n; 1 = ab 1. Punkt. Beispiel:
|
| Mmovavg(vd,n) | Nimmt einen Vektor vd, eine ganze Zahl n = Zeitraum, und gibt einen Vektor der modifizierten gleitenden Durchschnitte aus. Beispiel:
|
| Movavg(vd,back,forward[,missing]) | Nimmt einen Vektor vd und gibt den gleitenden Durchschnitt der angrenzenden Bereiche [i-back, i+forward] für einen Punkt i (i = die aktuelle Zeilennummer) aus. Die Option missing bestimmt, ob fehlende Werte ausgelassen werden sollen. Beispiel:
|
| Movcoef(v1,v2,back,forward[,missing]) | Nimmt zwei Vektoren v1 und v2 und gibt einen Vektor der gleitenden Korrelationskoeffizienten der angrenzenden Bereiche [i-back, i+forward] für einen Punkt i (i = die aktuelle Zeilennummer) aus. Die Option missing bestimmt, ob fehlende Werte ausgelassen werden sollen. Beispiel:
|
| Movrms(vd,back[,forward]) | Nimmt einen Vektor vd und gibt den quadratischen Mittelwert (RMS) der angrenzenden Bereiche [i-back, i+forward] für einen Punkt i (i = die aktuelle Zeilennummer) aus. Beispiel:
|
| Movslope(vx,vy[,n]) | Nimmt zwei Vektoren, vx (unabhängig) und vy (abhängig), gibt einen Vektor der gleitenden Steigung bei jedem Punkt aus. Optional legt n die Fensterbreite fest (sollte > 1 sein). Wenn n gerade ist, wird 1 addiert. Wenn n nicht festgelegt ist, gibt die Funktion einen Vektor von einem Wert aus, der die Steigung des linearen Fits der Eingabe ist. Beispiel:
|
| Tmovavg(vd,n[,missing]) | Nimmt einen Vektor vd und eine ganze Zahl n = Zeitraum, gibt einen Vektor des dreieckigen gleitenden Durchschnitts aus. Die Option missing bestimmt, ob fehlende Werte ausgelassen werden sollen. Beispiel:
|
| Wmovavg(vd,vw) | Nimmt einen Vektor vd (zu glättende Daten) und einen Vektor vw (indizierter Gewichtungsfaktor), gibt einen Vektor der gewichteten gleitenden Durchschnitte aus. Beispiel:
|
| Name | Brief Description |
|---|---|
| betacdf(x,a,b[,tail]) | Berechnet die kumulative Beta-Verteilungsfunktion bei x, mit den Parametern a und b. a und b müssen positiv sein, und x muss auf dem Intervall [0,1] liegen. tail bestimmt, ob die ausgegebene Wahrscheinlichkeit die untere oder die obere ist. |
| binocdf(k,n,p) | Berechnet die untere, obere und Punktwahrscheinlichkeit bei einem gegebenen Wert k, verbunden mit einer Binomialverteilung mit Hilfe der entsprechenden Parameter n, p.
|
| bivarnormcdf(x,y,corre) | Berechnet die untere Wahrscheinlichkeit für die bivariate Normalverteilung.
|
| chi2cdf(x,df[,tail]) | Berechnet die untere/obere Wahrscheinlichkeit für die Chi-Quadrat-Verteilung mit realen Freiheitsgraden df. |
| foldnormcdf(x,mu,sigma) | Berechnet die untere Wahrscheinlichkeit für die gefaltete Normalverteilung. |
| fcdf(f,ndf,fdf[,tail]) | Berechnet die kumulative F-Verteilung bei f mit Freiheitsgraden der Zählervarianz ndf und Nennervarianz fdf. tail bestimmt, ob die ausgegebene Wahrscheinlichkeit die untere oder die obere ist. |
| gamcdf(g,a,b[,tail]) | Berechnet die untere/obere Wahrscheinlichkeit für Gammavariate g mit realen Freiheitsgraden mit Hilfe des Formparameters a und des Skalenparameters b. tail bestimmt, ob die ausgegebene Wahrscheinlichkeit die untere oder die obere ist. |
| hygecdf(k,m,n,l) | Berechnet die unteren Wahrscheinlichkeiten bei einem gegebenen Wert, verbunden mit einer hypergeometrischen Verteilung mit Hilfe der entsprechenden Parameter.
wobei n der Umfang der Grundgesamtheit, m die Anzahl der Erfolgszustände in der Grundgesamtheit und l die Anzahl der gezogenen Stichproben ist. |
| landaucdf(x,mu,sigma[,tail]) (2024b) |
Berechnet die kumulative Dichtefunktion für die Landau-Verteilung bei x und mit Lageparameter Mu und Skalierungsparameter Sigma. tail bestimmt, ob die ausgegebene Wahrscheinlichkeit die untere oder die obere ist. |
| logncdf(x,mu,sigma[,tail]) (2015 SR0) |
Berechnet die Wahrscheinlichkeiten bei einem festgelegten Endtyp tail in einem gegebenen Wert x, verbunden mit einer Lognormal-Verteilung mit Hilfe der entsprechenden Parameter mu und sigma. Untere Wahrscheinlichkeit wird ausgegeben, falls tail nicht angegeben ist. |
| ncbetacdf(x,a,b,lambda) | Berechnet die cdf mit unterer Wahrscheinlichkeit der nicht-zentralen Beta-Verteilung.
|
| ncchi2cdf(x,f,lambda) | Berechnet die Wahrscheinlichkeit, die mit der unteren Wahrscheinlichkeit der nicht-zentralen Chi-Quadrat-Verteilung verbunden ist.
|
| ncfcdf(f,df1,df2,lambda) | Berechnet die Wahrscheinlichkeit, die mit der unteren Wahrscheinlichkeit der nicht-zentralen Digamma- oder der Varianz-Verhältnis-Verteilung verbunden ist.
wobei
und |
| nctcdf(t,df,delta[,maxiter]) | Berechnet die untere Wahrscheinlichkeit für die nicht-zentrale Studentsche t-Verteilung.
|
| normcdf(x[,tail]) | Berechnet die Wahrscheinlichkeiten bei einem festgelegten Endtyp tail in einem gegebenen Wert x, verbunden mit einer kumulativen Normal-Verteilung. |
| poisscdf(k,lambda) | Berechnet die unteren Wahrscheinlichkeiten bei einem gegebenen Wert k, verbunden mit einer Poisson-Verteilung mit Hilfe der entsprechenden Parameter in lambda.
|
| srangecdf(q,v,group) | Berechnet die Wahrscheinlichkeit, die mit dem unteren Ende der Verteilung der studentisierten Bereichsstatistik verbunden ist.
wobei |
| tcdf(t,df[,tail]) | Berechnet die Wahrscheinlichkeiten des festgelegten Endtyps tail, verbunden mit einer kumulativen Verteilungsfunktion der Studenten-t-Verteilung mit den Freiheitsgraden df. |
| wblcdf(x,a,b) | Berechnet die untere Wahrscheinlichkeit der kumulativen Weibull-Verteilungsfunktion für den Wert x mit Hilfe der Parameter a und b.
wobei |
| Name | Brief Description |
|---|---|
| betapdf(x,a,b) | Gibt die Funktion der Wahrscheinlichkeitsdichte der Beta-Verteilung mit den Parametern a und b aus.
mit |
| binopdf(x,nt,p) (2015 SR0) |
Gibt die Funktion der Wahrscheinlichkeitsdichte der Binomialverteilung mit den Parametern nt und p aus.
wobei |
| cauchypdf(x,a,b) (8,6 SR0) |
Cauchy-Wahrscheinlichkeitsdichtefunktion (alias Lorentz-Verteilung).
|
| exppdf(x,lambda) (8,6 SR0) |
Gibt die Funktion der Wahrscheinlichkeitsdichte der Exponentialverteilung mit Ratenparameter lambda aus, ausgewertet bei Wert X.
|
| foldnormpdf(x,mu,sigma) | Berechnet die Funktion der Wahrscheinlichkeitsdichte bei jedem der Werte in X mit Hilfe der gefalteten Normalverteilung mit Mittelwert mu und Standardabweichung sigma.
|
| gampdf(x,a,b) (8,6 SR0) |
Gibt die Gamma-Wahrscheinlichkeitsdichte mit den Parametern a und b aus.
Um die Skalen- und Formparameter a und b aus einem Datensatz mit Gamma-Verteilung zu ermitteln, können Sie die Schätzungsfunktion gamfit verwenden. |
| ks2d(vx, vy[,bandwidth, grid, interp, binned]) (2020) |
Gibt die 2D-Kernel-Dichte bei Punkt (x, y) mit festgelegter Bandbreiten- und Dichtemethode aus, wobei vx ein Vektor der X-Koordinatenwerte und vy ein Vektor der Y-Koordinatenwerte ist. Optionen für Bandbreitenmethode, Gitternetz (nur Bandbreitenmethode), Interpolation und Dichte (nur anwendbar, wenn interp = 1 (wahr)).
wobei n die Anzahl der Elemente in Vektor vx oder vy ist, der Index i auf das i-te Element in vx oder vy verweist und optimale Skalen (wx, wy) von der Schätzungsfunktion kernel2width bestimmt werden. |
| ks2density(x,y,vx,vy,wx,wy) (2015 SR0) |
Gibt die 2D-Kerneldichte bei Punkt (x, y) aus in Bezug auf eine Funktion, die durch den Datensatz (vx, vy) mit der Skala (wx, wy) errzeugt wurde.
wobei n die Anzahl der Elemente in Vektor vx oder vy ist, der Index i auf das i-te Element in vx oder vy verweist und optimale Skalen (wx, wy) von der Schätzungsfunktion kernel2width bestimmt werden. |
| ksdensity(x,vx,w) (2015 SR0) |
Gibt die Kerneldichte bei x für einen gegebenen Vektor vx mit einer Bandbreite w aus.
wobei n die Größe des Vektors vX und K die Kernelfunktion ist, Origin die normale Kernelfunktion (Gaussian) verwendet, |
| landaupdf(x,mu,sigma) (2024b) |
Berechnet die Funktion der Wahrscheinlichkeitsdichte bei jedem der Werte in X mit Hilfe der Landau-Verteilung mit Lageparameter mu und Skalierungsparameter sigma. |
| lappdf(x,mu,b) (8,6 SR0) |
Wahrscheinlichkeitsdichtefunktion nach Laplace. |
| lognpdf(x,mu,sigma) (8,6 SR0) |
Gibt die Werte bei X der Lognormal-Funktion der Wahrscheinlichkeitsdichte mit den Verteilungsparametern mu und sigma aus.
|
| normpdf(x,mu,sigma) (8,6 SR0) |
Berechnet die Funktion der Wahrscheinlichkeitsdichte bei jedem der Werte in X mit Hilfe der Normalverteilung mit Mittelwert mu und Standardabweichung sigma.
|
| poisspdf(x,lambda) (8,6 SR0) |
Berechnet die Poisson-Funktion der Wahrscheinlichkeitsdichte bei jedem der Werte in X mit Hilfe der Mittelwertparameter in lambda.
|
| wblpdf(x,a,b) (8,6 SR0) |
Gibt die Funktion der Wahrscheinlichkeitsdichte der Weibull-Verteilung mit den Parametern a und b aus.
Um die Skalen- und Formparameter a und b aus einem Datensatz mit Weibull-Verteilung zu ermitteln, können Sie die Schätzungsfunktion wblfit verwenden. |
| Name | Brief Description |
|---|---|
| betainv(p,a,b) | Gibt die Inverse der kumulativen Verteilungsfunktion für eine festgelegte Beta-Verteilung aus. |
| chi2inv(p,df) | Berechnet die Inverse der kumulativen Chi-Quadrat-Dichtefunktion für die entsprechenden Wahrscheinlichkeiten in X mit Parametern, festgelegt durch nu.
|
| finv(p,df1,df2) | Berechnet die Inverse der kumulativen F-Dichtefunktion bei p mit den Parametern df1 und df2.
wobei |
| foldnorminv(p,mu,sigma) | Berechnet die Abweichung x, verbunden mit der gegebenen unteren Wahrscheinlichkeit p, der gefalteten Normalverteilung, mit den Verteilungsparametern mu und sigma. |
| gaminv(p,a,b) | Berechnet die Inverse der kumulativen Gamma-Dichtefunktion bei p mit den Parametern a und b.
wobei |
| Landauinv(p,mu,sigma) (2024b) |
Berechnet die Inverse der kumulativen Landau-Dichtefunktion bei p mit Lageparameter mu und Skalierungsparameter sigma. |
| logninv(p,mu,sigma) (2015 SR0) |
Berechnet die normierte Abweichung x, verbunden mit der gegebenen unteren Wahrscheinlichkeit p, der Lognormal-Verteilung mit den Parametern mu und sigma.
wobei |
| norminv(p) | Berechnet die normierte Abweichung x, verbunden mit der gegebenen unteren Wahrscheinlichkeit p, der standardisierten Normalverteilung.
wobei |
| srangeinv(p,v,ir) | Berechnet die normierte Abweichung x, verbunden mit der unteren Wahrscheinlichkeit der Verteilung der studentisierten Bereichsstatistik.
|
| tinv(p,df) | Berechnet die Abweichung, die mit der unteren Wahrscheinlichkeit der studentisierten t-Verteilung mit realen Freiheitsgraden verbunden ist.
|
| wblinv(p,a,b) | Berechnet die inverse kumulative Funktion der Weibull-Verteilung für die gegebene Wahrscheinlichkeit mit Hilfe der Parameter a und b.
|
Zwei Funktionen in dieser Kategorie, rnd()/ran() und grnd(), geben einen Wert aus. Alle anderen Funktionen in dieser Kategorie geben einen Bereich aus.
| Hinweis: Der Algorithmus für Origins Methoden zum Erzeugen von Zufallszahlen wurde für Version 2016 geändert. Weitere Informationen finden Sie in der Dokumentation für die Systemvariable @ran. |
| Name | Brief Description |
|---|---|
| Data(x1,x2,inc) | Nimmt zwei Werte x1 und x2 und erstellt einen Datensatz, der von x1 bis x2 reicht und ein Inkrement inc aufweist. Wenn x1 = x2, gibt die Funktion inc die Anzahl der Punkte mit Werten = x1 aus. Standard für inc = 1. Beispiele: col(A) = data(0,100,5) füllt Spalte A mit Zahlen von 0 bis 100 mit dem Inkrement = 5.
|
| grnd() | Gibt einen Wert aus einer normalverteilten (Gaussian) Stichprobe aus, inklusive Nullmittelwert und Standardabweichung der Einheit. Der Anfangswert und die Wertesequenz sind die gleiche bei jeder Origin-Sitzung. Es ist kein Argument notwendig. Im Allgemeinen wird die Funktion verwendet, um einen Zufallswert aus einer Normalverteilung mit bekanntem Mittelwert und bekannter Standardabweichung auszugeben mit Hilfe des folgenden Ausdrucks: grnd()*sd+m. Beispiel:
|
| normal(npts[,seed]) | Gibt einen Bereich von npts aus. Die Werte sind Zufallszahlen mit Normalverteilung (Mittelwert null, Einheit Standardabweichung). Wenn seed ausgelassen wird, wird stattdessen bei jedem Aufruf der Funktion eine anderes "Seed" verwendet. Kann verwendet werden, um eine Spalte mit normalverteilten Zufallswerten zu füllen, bei gegebenen Mittelwert und Standardabweichung: normal(npts)*sd+m. Beispiel:
|
| pattern(vd, onerepeat, seqrepeat) und pattern(x1,x2,inc,onerepeat,seqrepeat) | Gibt die erzeugten numerischen oder Textdaten mit Muster aus. pattern(vd, onerepeat, seqrepeat) nimmt eine Reihe von Eingabezeichenketten vd und wiederholt jedes Element in vd onerepeat-mal und wiederholt dann die gesamte Zeichenkettenreihe seqrepeat-mal. pattern(x1,x2,inc,onerepeat,seqrepeat) erstellt einen Datensatzbereich von x1 bis x2 mit dem Inkrement inc. Jedes Element im Datensatz wird onerepeat-mal wiederholt. Dann wird der gesamte Datensatz seqrepeat-mal wiederholt. Beachten Sie, dass die Elemente in der Zeichenkettenreihe durch Hochstrich (|), Komma(,) oder Leerzeichen bzw. eine Bereichsvariable getrennt sein können. Beispiel:
|
| Poisson(n, mean [,seed]) | Gibt n zufällige ganze Zahlen mit Poisson-Verteilung und Mittelwert aus. Optional bietet seed einen "Seed" für den Zahlenerzeuger. Beispiel:
|
| ran([seed]) und rnd([seed]) | Gibt einen Wert zwischen 0 und 1 aus einer gleichverteilten Stichprobe aus. Wenn die Option seed positiv ist, wird das "Seed" festgelegt und 0 ausgegeben. Wenn seed ≤ 0 ist oder wenn kein Argument bereitsteht, wird die nächste Zahl in der Sequenz der Zufallszahlen ausgegeben. |
| uniform(npts [,seed]) und uniform(npts, vd) | Gibt einen Bereich von npts aus. Die Option seed kann ein Wert, ein Datenbereich, getrennte Zeichenketten ("|", "," oder Leerzeichen) oder eine Zeichenketten-Array sein. Wenn seed ein Wert ist, werden gleichverteilte Zufallszahlen ausgegeben. Wenn seed ein Datenbereich oder ein Zeichenketten-Array ist, werden die ausgegebenen Werte zufällig aus dem Datenbereich oder den Zeichenketten gewählt. Wenn seed ausgelassen wird, wird stattdessen bei jedem Aufruf der Funktion eine anderes "Seed" verwendet. Diese Funktion akzeptiert auch einen Vektor vd als Argument. |
| Name | Brief Description |
|---|---|
| Category(vd)$ (2020b) |
Nimmt einen Vektor vd der kategorialen Daten und gibt alle Kategorien in einer Arbeitsblattspalte aus. Kategorienreihenfolge folgt der Quellspalte. Beispiele:
|
| Catindex(vd) (2020b) |
Nimmt einen Vektor vd der kategorialen Daten und gibt den Kategorienindex für jeden seiner Elemente in einer Arbeitsblattspalte aus. Beispiele:
|
| Catrows(vd[,option]) (2024b) |
Nimmt einen Vektor vd der kategorialen Daten und gibt eine mit senkrechtem Strich getrennte Liste aller Zeilenindizes nach Kategorie aus. Optionale Option bestimmt die Ausgabe von allen/erstem/letzten Index für jede Kategorie. Kategorienreihenfolge folgt der Quellspalte. Beispiele:
|
| Cattext(n,vd)$ (2020b) |
Nimmt einen Vektor vd der kategorialen Daten und gibt den n-ten Kategoriewert aus. Beispiele:
|
| Findmasks(vd) | Nimmt einen Vektor vd, der maskierte Daten enthält, und gibt einen Vektor der Indizes der maskierten Punkte aus. Beispiel:
|
| Firstpoint(vd) | Nimmt einen Vektor vd, gibt den ersten Wert des Datensatzes vd aus. Beispiel:
|
| Idx(vBool) | Wertet den Bedingungsausdruck vBool aus, der einen einzelnen Vektor beinhaltet, und gibt einen Vektor mit ganzen Zahlen aus, der die Zeilenindizes aller Aufzeichnungen enthält, die die Bedingung erfüllen. Beispiele:
|
| Index(d,vd[,n]) | Nimmt einen Vektor vd der streng monotonischen Daten, gibt den Index des Datenpunkts d aus. Wenn die Option n = 0 (Standard) den Wert findet, der gleich oder am nächsten dem Wert von d ist; n = 1 sucht nach ≤ d; n = 2 sucht nach ≥ d. Wenn vd nicht streng monotonisch ist oder Text enthält, wird -2 ausgegeben. Beispiel:
|
| Lastpoint(vd) | Nimmt einen Vektor vd (Datensatz), gibt den letzten Wert des Datensatzes vd aus. Beispiel:
|
| List(val,vd) | Nimmt einen Vektor vd, gibt die Indexnummer des Datensatzes für das erste Auftreten von val aus. Wenn val nicht gefunden wird, gibt die Funktion 0 aus. Beispiel:
|
| lookup(str$,vs,vref[,option,Case])[$] (2015 SR0) |
Sucht nach der Zeichenkette str$ in Vektor vs und gibt den Wert in Vektor vref (numerisch oder Zeichenkette) mit dem gleichen Index aus. Die Präzision der Übereinstimmung wird von der option bestimmt. Wenn Case = 0 (Standard), berücksichtigt die Funktion keine Groß- und Kleinschreibung. Beispiel:
|
| table(vd,vref,d[,option])[$] (2015 SR0) |
Sucht nach dem Wert d in Vektor vd, gibt den Wert in vref mit der gleichen Indexnummer aus. Der Ausgabewert kann numerisch oder eine Zeichenkette sein, abhängig von vref. Der Parameter option modifiziert die Suche nach Parameter d: -1 (Standard) = Funktion führt eine lineare Interpolation für vd vs. vref durch und gibt den interpolierten Wert aus; 0 = sucht den nächsten Wert, der ≤ d ist; 1 = sucht den nächsten Wert, der ≥ d ist; 2 = sucht den nächsten oder gleichen Wert. |
| unique(vs[, sort, occurrence, sort2]) (2018b) |
Nimmt einen Vektor vs und gibt die eindeutigen Werte aus. Der Parameter sort entscheidet, ob die ausgegebenen Werte sortiert werden sollen: 1 (Standard) = aufsteigend sortieren; 0 = ohne sortieren; 2 = absteigend sortieren. Der Parameter occurrence legt fest, wie die duplizierten Werte reduziert werden: 0 (Standard) = der erste duplizierte Wert bleibt; 1 = der letzte duplizierte Wert bleibt. sort2 bestimmt, wie mit dem Auftreten umgegangen wird: 0 (Standard) = kein Sortieren des Auftretens = Auftreten aufsteigend sortieren. 2 = Auftreten absteigend sortieren. Beispiel:
|
| ReportCell(sBook$,sSheet$,sTable$,sRowRef$,sColRef$) (2021b) |
Zugriff auf Zelle in Berichtstabelle durch festgelegten Mappenname sBook, Blattname sSheet, Tabellenname sTable und Zellen- und Spaltenreferenzen sRowRef bzw. sColRef. Beispiel: Gauss Fit auf Daten in Book1 durchführen mit folgender Formel:
Hinweis: Diese Funktion kann nicht in Zellenformeln verwendet werden. |
| Xindex(x,vd[,option]) | Nimmt einen Vektor vd (Y-Datensatz), gibt die Zeilenindexnummer des Werts im X-Datensatz verbunden mit vd aus, die am nächsten an Wert x liegt. option bestimmt, welcher Index ausgegeben wird: 0 (Standard) = gleich oder am nächsten links; 1 = gleich oder am nächsten rechts; 2 = gleich oder am nächsten links oder rechts. Anforderungen: (1) vd muss eine zugewiesene Y-Spalte sein; (2) der Name von vd muss einem tatsächlichen Y-Datensatz entsprechen; (3) der X-Datensatz muss in aufsteigender Reihenfolge sortiert sein. Beispiel:
|
| Xvalue(n,vd) | Nimmt einen Vektor vd (Y- oder Z-Datensatz), gibt den entsprechenden X-Wert bei Zeilennummer n aus. Beispiel:
|
| Errof(vd) | Nimmt einen Vektor vd (Datensatz), gibt den Datensatz (xEr/yEr), der die Fehlerwerte von vd enthält, aus. Beispiel:
|
| hasx(vd) | Nimmt einen Datensatz vd und gibt 1 aus, wenn vd gegen einen X-Datensatz im aktiven (Diagramm-)Layer gezeichnet ist; falls nicht, wird 0 ausgegeben. Beispiel:
|
| IsMasked(n,vd) | Nimmt einen Vektor vd und, wenn n = 0, gibt die Anzahl der maskierten Punkte aus. Wenn n = Indexnummer des Datenpunkts, wird 1 ausgegeben, falls maskiert, 0, falls nicht maskiert. Beispiel:
|
| Xof(vd) | Nimmt einen Vektornamen vd, was ein Y-Datensatz mit einem verbundenen X-Datensatz ist, und gibt eine Zeichenkette aus, die den Namen des X-Datensatzes enthält. Beispiel:
|
| Name | Brief Description |
|---|---|
| asc(str$) | Nimmt eine ganzzahlige Zeichenkette und gibt den ASCII-Code (dezimal) für das erste Zeichen in der Zeichenkette aus. Diese Funktion tut das Gleiche mit der Funktion code. Beispiel:
|
| corr(vx,vy,k[, n]) | Nimmt zwei Datensätze vx und vy, eine Größe der Zeitverschiebung k und gibt die Korrelation zwischen zwei Datensätzen aus. Die Option n ist die Anzahl der Punkte. Der Parameter der Zeitverschiebungsgröße k kann ein Skalar oder ein Vektor sein. Wenn k ein Vektor ist, gibt die Funktion einen Vektor aus; wenn es ein Skalar ist, wird ein Skalar ausgegeben. Beispiel:
|
| dropNA(vd[, text]) | Nimmt einen Vektor vd und entfernt die fehlenden und maskierten Werte. Optionaler Parameter text bestimmt, wie mit dem Text umgegangen wird. Beispiel:
|
| join(rA, rB, ...) | Nimmt zwei oder mehr Bereiche, gekennzeichnet als rA1:rA2, rB1:rB2,... und verbindet sie zu einem einzelnen Datensatz. Beispiel:
|
| peaks(vd, width, minht) | Nimmt einen Vektor vd, gibt einen Datensatz der Peakindizes aus, der mit width und minht gefunden wird. width ist die Anzahl der Punkte zu jeder Seite des Testpunkts. minht ist Einheiten der Y-Achse. Ein Peak bei Index i ist minht größer als der Datenwert bei (i-width) oder (i+width). Beispiel:
|
| rank(vd[, n]) | Nimmt einen Datenatz vd, sortiert ihn und gibt den Index mit Rangfolge aus. Wenn n = 0 (Standard), wird vd in aufsteigender Reihenfolge sortiert; wenn n = 1 in absteigender Reihenfolge. Wenn in vd duplizierte Werte existieren, wird die durchschnittliche Anzahl der Indizes mit Rangfolge für jeden duplizierten Wert ausgegeben. Beispiel:
|
| reverse(vd) | Nimmt einen Vektor vd und kehrt die Ordnung um. Beispiel:
|
| sort(vd) | Nimmt einen Datensatz, sortiert ihn in aufsteigender Reihenfolge und gibt ihn aus. Beispiel:
|
| treplace(vd,val1,val2[, cnd]) | Ersetzt einen Datensatzwert mit einem anderen, wenn die Bedingungen cnd erfüllt werden. Nimmt einen Datensatz vd und vergleicht jeden Wert mit val1 in Bezug auf die Option cnd. Wenn der Vergleich wahr ist, wird mit val2 (oder -val2) ersetzt; wenn er falsch ist, wird der Wert beibehalten oder mit einem fehlenden Wert ("--") ersetzt. |
| Name | Brief Description |
|---|---|
| airy_ai(x) | Wertet eine Approximation an die Airy Funktion Ai(x) aus. |
| airy_ai_deriv(x) | Wertet eine Approximation der Ableitung der Airy Funktion Ai(x) aus. |
| airy_bi(x) | Wertet eine Approximation an die Airy Funktion Bi(x) aus. |
| airy_bi_deriv(x) | Wertet eine Approximation der Ableitung der Airy Funktion Bi(x) aus. |
| Name | Brief Description |
|---|---|
| bessel_i0(x) | Bessel i0. Wertet eine Approximation an die modifizierte Bessel-Funktion der ersten Art I0(x) aus. |
| bessel_i0_scaled(x) | Bessel i0 skaliert. Wertet eine Approximation an 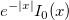 aus. aus. |
| bessel_i1(x) | Bessel i1. Wertet eine Approximation an die modifizierte Bessel-Funktion der ersten Art 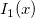 aus. aus. |
| bessel_i1_scaled(x) | Bessel i1 skaliert. Wertet eine Approximation an 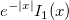 aus. aus. |
| bessel_i_nu(x,nu) | Bessel i nu. Wertet eine Approximation an die geänderte Bessel-Funktion der ersten Art I /4(x) aus. /4(x) aus. |
| bessel_i_nu_scaled(x,nu) | Bessel i nu skaliert. Wertet eine Approximation an die modifizierte Bessel-Funktion der ersten Art 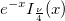 aus. aus. |
| bessel_j0(x) | Bessel j0. Wertet die Bessel-Funktion der ersten Art 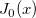 aus. aus. |
| bessel_j1(x) | Bessel j1. Wertet eine Approximation an die Bessel-Funktion der ersten Art 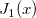 aus. aus. |
| bessel_k0(x) | Bessel k0. Wertet eine Approximation an die modifizierte Bessel-Funktion der zweiten Art 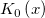 aus. aus. |
| bessel_k0_scaled(x) | Bessel k0 skaliert. Wertet eine Approximation an 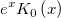 aus. aus. |
| Bessel_k1(x) | Bessel k1. Wertet eine Approximation an die modifizierte Bessel-Funktion der zweiten Art 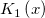 aus. aus. |
| bessel_k1_scaled(x) | Bessel k1 skaliert. Wertet eine Approximation an 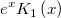 aus. aus. |
| bessel_k_nu(x,nu) | Bessel k nu. Wertet eine Approximation an die modifizierte Bessel-Funktion der zweiten Art 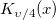 aus. aus. |
| bessel_k_nu_scaled(x,nu) | Bessel k nu skaliert. Wertet eine Approximation an die modifizierte Bessel-Funktion der zweiten Art 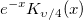 aus. aus. |
| bessel_y0(x) | Bessel y0. Wertet die Bessel-Funktion der zweiten Art aus, 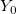 , x > 0. Die Approximation basiert auf Tschebyscheff-Erweiterungen. , x > 0. Die Approximation basiert auf Tschebyscheff-Erweiterungen. |
| bessel_y1(x) | Bessel y1. Wertet die Bessel-Funktion der zweiten Art aus, 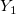 , x > 0. Die Approximation basiert auf Tschebyscheff-Erweiterungen. , x > 0. Die Approximation basiert auf Tschebyscheff-Erweiterungen. |
| Name | Brief Description |
|---|---|
| erf(x) | Die Fehlerfunktion (oder das Fehlerintegral der Normalverteilung). |
| erfc(x) | Berechnet einen Näherungswert für das Komplement der Fehlerfunktion. |
| erfcinv(dy) | Berechnet den Wert der inversen komplementären Fehlerfunktion für das festgelegte y. |
| erfcx(x) | Die skalierte komplementäre Fehlerfunktion. |
| erfi(c) | Nimmt eine komplexe oder reale Zahl und gibt die imaginäre Fehlerfunktion aus. |
| erfinv(dy) | Die inverse Fehlerfunktion. |
| Name | Brief Description |
|---|---|
| gamma(x) | Gamma-Funktion. Wertet 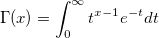 aus. aus. |
| incomplete_gamma(a,x) | Unvollständige Gamma-Funktion. |
| log_gamma(x) | Log-Gamma-Funktion. Wertet 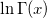 .x > 0 aus. .x > 0 aus. |
| real_polygamma(x,k) | Polygamma-Funktion. Wertet eine Approximation an die k-te Ableitung der psi-Funktion 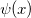 aus. aus. |
| Name | Brief Description |
|---|---|
| cos_integral(x) | NAG: Cosinus-Integral-Funktion. Wertet 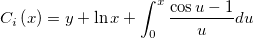 aus. aus. |
| cumul_normal(x) | Wertet die kumulative Normalverteilungsfunktion aus. |
| cumul_normal_complem(x) | Wertet einen Näherungswert für das Komplement der kumulativen Normalverteilungsfunktion aus. |
| elliptic_integral_rc(x,y) | NAG: Elliptisches Integral der ersten Art. Berechnet einen Näherungswert für das Integral 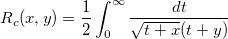 . . |
| elliptic_integral_rd(x,y,z) | NAG: Symmetrisiertes elliptisches Integral der zweiten Art. Berechnet einen Näherungswert für das Integral 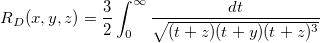 . . |
| elliptic_integral_rf(x,y,z) | NAG: Symmetrisiertes elliptisches Integral der ersten Art Berechnet eine Approximation an das Integral 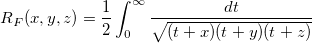 . . |
| elliptic_integral_rj(x,y,z,r) | NAG: Symmetrisiertes elliptisches Integral der dritten Art. Berechnet eine Approximation an das Integral 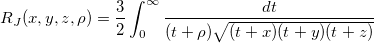 . . |
| exp_integral(x) | NAG: Exponentielle Integral-Funktion. Wertet 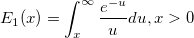 aus. aus. |
| fresnel_c(x) | NAG: Fresnel-Integral-Funktion C. Wertet eine Approximation an das Fresnel-Integral 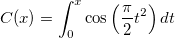 aus. aus. |
| fresnel_s(x) | NAG: Fresnel-Integral-Funktion S. Wertet eine Approximation an das Fresnel-Integral 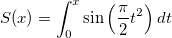 aus. aus. |
| sin_integral(x) | NAG: Sinus-Integral-Funktion. Wertet 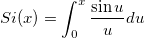 aus. aus. |
| Name | Brief Description |
|---|---|
| kelvin_bei(x) | Wertet eine Approximation an die Kelvin-Funktion bei x aus. |
| kelvin_ber(x) | Wertet eine Approximation an die Kelvin-Funktion ber x aus. |
| kelvin_kei(x) | Wertet eine Approximation an die Kelvin-Funktion kei x aus. |
| kelvin_ker(x) | Wertet eine Approximation an die Kelvin-Funktion ker x aus. |
| Name | Brief Description |
|---|---|
| jacobian_theta(k,x,q) | NAG: Jacobische Thetafunktion. Berechnet den Wert von einer der Jacobischen Thetafunktionen 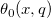 , , 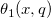 , , 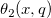 , , 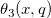 oder oder 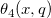 für ein reales Argument x und nicht-negatives q ≤ 1. für ein reales Argument x und nicht-negatives q ≤ 1. |
| lambertW(x[,branch,offset]) | Berechnet einen Näherungswert für die realen Zweige der W-Funktion nach Lambert. |
Multiparametrische Funktionen in dieser Kategorie werden als Standardfunktionen für Origins nichtlineare Anpassung verwendet. Sie können die Gleichung, eine Beispielkurve und die Funktionsdetails für jede multiparametrische Funktion anzeigen, indem Sie NLFit öffnen (Analyse: Anpassen: Nichtlinearer Fit). Wählen Sie dann die gewünschte Funktion aus der Auswahlliste Funktion.
Zusätzliche Dokumentation zu allen verfügbaren multiparametrishen Funktionen von Origins nichtlinearem Kurvenfit, siehe diese PDF auf der Webseite von OriginLab. Dieses Dokument enthält die mathematische Beschreibung, eine Beispielkurve, eine Erläuterung der Parameter und die Syntax der LabTalk-Funktion für jede multiparametrische Funktion.
| Name | Brief Description |
|---|---|
| Allometric1(x,a,b) | Klassisches Freundlich-Modell, ist in der Allometriestudie verwendet worden.
|
| Beta(x,y0,xc,A,w1,w2,w3) | Beta-Peakfunktion zur Verwendung in Chromatographie und Spektroskopie.
|
| Boltzmann(x, A1, A2, x0, dx) | Boltzmann-Funktion - erzeugt eine sigmoidale Kurve.
|
| dhyperbl(x,P1,P2,P3,P4,P5) | Doppelte rechteckige Hyperbelfunktion.
|
| ExpAssoc(x,y0,A1,t1,A2,t2) | Exponentielle Assoziationsgleichung mit zwei Phasen.
|
| ExpDec1(x,y0,A1,t1) | Exponentielle Zerfallsfunktion mit einer Phase und zeitkonstantem Parameter.
|
| ExpDec2(x,y0,A1,t1,A2,t2) | Exponentielle Zerfallsfunktion mit zwei Phasen und zeitkonstantem Parameter.
|
| ExpDec3(x,y0,A1,t1,A2,t2,A3,t3) | Exponentielle Zerfallsfunktion mit drei Phasen und zeitkonstantem Parameter.
|
| ExpGrow1(x,y0,x0,A1,t1) | Einphasiges exponentielles Wachstum mit Zeitverschiebung, x0 sollte fest sein.
|
| ExpGrow2(x, y0, x0, A1, t1, A2, t2) | Einphasiges exponentielles Wachstum mit Zeitverschiebung, x0 sollte fest sein.
|
| Gauss(x, y0, xc, w, A) | Flächenversion der Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Fläche) |
| GaussAmp(x,y0,xc,w,A) | Amplitudenversion der Gaussian-Peakfunktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Amplitude) |
| Hyperbl(x, P1, P2) | Hyperbel-Funktion, auch das Michaelis-Menten-Modell in Enzymkinetik.
|
| Logistic(x, A1, A2, x0, p) | Logistische Dose-Response in Pharmakologie/Chemie. Auch als 4PL oder 4PLC bezeichnet.
|
| LogNormal(x,y0,xc,w,A) | Wahrscheinlichkeitsdichtefunktion der Zufallsvariable, deren Logarithmus normalverteilt ist.
|
| Lorentz(x, y0, xc, w, A) | Lorentz-Peakfunktion mit Glockenform und viel breiteren Enden als die Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = FWHM, A = Fläche) |
| Poisson(x,y0,r) | Wahrscheinlichkeitsdichtefunktion nach Poisson, eine diskrete Wahrscheinlichkeitsverteilung.
|
| Pulse(x, y0, x0, A, t1, P, t2) | Exponentielle Pulse-Funktion (x >= x0 ? y : 0).
|
| Rational0(x,a,b,c) | Rationale Funktion mit Zähler 1. Ordnung und Nenner 1. Ordnung.
|
| Sine(x,y0,xc,w,A) | Die Sinusiodfunktion schwingt um einen festgelegten Wert.
|
| Voigt(x,y0,xc,A,wG,wL) | Faltung einer Gaussian-Funktion und einer Lorentz-Funktion. (y0 = Verschiebung, xc = Zentrum, A = Fläche, wG = Gaussian FWHM, wL = Lorentz FWHM) |
| Name | Brief Description |
|---|---|
| Circle(x,y,xc,yc,r) | Implizite Kreisgleichung mit den Parametern Kreiszentrum und -radius.
|
| Ellipse(x,y,xc,yc,a,b) | Implizite Ellipsengleichung, deren Haupt- und Nebenachsen mit den XY-Achsen übereinstimmen.
|
| ModDiode(V,I,T,Is,Rs,n,Rsh) | Implicit modified diode equation.
|
| PlaneMod(x,y,z,theta,phi,d) | Modifizierte implizite Ebenenfunktion, die durch die Richtung ihrer Normalverteilung definiert wird.
|
| SolarCellIV(V,I,T,Is,Rs,n,Rsh,IL) | Solar cell I-V curve.
|
| Name | Brief Description |
|---|---|
| Asymptotic1(x,a,b,c) | Asymptotisches Regressionsmodell - 1. Parameterisierung.
|
| BoxLucas1(x,a,b) | Box-Lucas-Modell, identisch mit ein-phasiger Assoziationsgleichung mit Nullverschiebung.
|
| BoxLucas1Mod(x,a,b) | Eine Parametrisierung des Box-Lucas-Modells.
|
| BoxLucas2(x,a1,a2) | Box-Lucas-Modell für zwei Phasen.
|
| Chapman(x,a,b,c) | Chapman-Richards-Funktion zum Beschreiben der kumulativen Wachstumskurve.
|
| Exp1p1(x,A) | Einparametrische Exponentialfunktion.
|
| Exp1p2(x,A) | Einparametrische Exponentialfunktion.
|
| Exp1p2Md(x,B) | Einparametrische Exponentialfunktion.
|
| Exp1P3(x,A) | Einparametrische Exponentialfunktion.
|
| Exp1P3Md(x,B) | Einparametrische Exponentialfunktion.
|
| Exp1P4(x,A), | Einparametrische asymptotische Exponentialfunktion.
|
| Exp1P4Md(x,B) | Eine weitere Form der einparametrischen asymptotischen Exponentialfunktion.
|
| Exp2P(x,a,b) | Zweiparametrische Exponentialfunktion.
|
| Exp2PMod1(x,a,b), | Zweiparametrische Exponentialfunktion.
|
| Exp2PMod2(x,a,b), | Zweiparametrische Exponentialfunktion.
|
| Exp3P1(x,a,b,c), | Invertierte verschobene Exponentialfunktion.
|
| Exp3P1Md(x,a,b,c), | Eine weitere Form der invertierten verschobenen Exponentialfunktion.
|
| Exp3P2(x,a,b,c), | Exponentialfunktion, deren Exponent ein Polynom 2. Ordnung ist.
|
| ExpAssoc(x,y0,A1,t1,A2,t2) | Exponentielle Verknüpfungsgleichung mit zwei Phasen.
|
| ExpAssoc1(x,TD,Yb,A,Tau) (2017 SR0) |
Exponentielle Assoziationsgleichung mit einer Phase.
|
| ExpAssoc2(x,TD1,TD2,Yb,A1,A2,Tau1,Tau2) (2017 SR0) |
Biphasische exponentielle Assoziationsgleichung.
|
| nlf_ExpAssocDelay1(x,TD,Yb,A,Tau) (2017 SR0) |
Exponentielle Assoziationsgleichung mit einer Phase und Plateau vor Beginn des Exponentials.
|
| ExpAssocDelay2(x,TD1,TD2,Yb,A1,A2,Tau1,Tau2) (2017 SR0) |
Biphasische exponentielle Assoziationsgleichung mit Plateau vor Beginn des Exponentials.
|
| Exponential(x,y0,A,R0) | Exponentielle Wachstumsfunktion mit dem Parameter Ratenkonstante.
|
| ExpDec1(x,y0,A1,t1) | Exponentielle Zerfallsfunktion mit einer Phase und zeitkonstantem Parameter.
|
| ExpDec2(x,y0,A1,t1,A2,t2) | Exponentielle Zerfallsfunktion mit zwei Phasen und zeitkonstantem Parameter.
|
| ExpDec3(x,y0,A1,t1,A2,t2,A3,t3) | Exponentielle Zerfallsfunktion mit drei Phasen und zeitkonstantem Parameter.
|
| ExpDecay1(x,y0,x0,A1,t1) | Einphasige exponentielle Zerfallsfunktion mit Zeitverschiebung, x0 sollte fest sein.
|
| ExpDecay2(x, y0, x0, A1, t1, A2, t2) | Zweiphasige exponentielle Zerfallsfunktion mit Zeitverschiebung, x0 sollte fest sein.
|
| ExpDecay3(x,y0,x0,A1,t1,A2,t2,A3,t3) | Dreiphasige exponentielle Zerfallsfunktion mit Zeitverschiebung, x0 sollte fest sein.
|
| ExpGro1(x,y0,A1,t1) | Einphasige exponentielle Wachstumsfunktion mit Parameter Zeitkonstante.
|
| ExpGro2(x,y0,A1,t1,A2,t2) | Two-phase exponential growth function with time constant parameters.
|
| ExpGro3(x,y0,A1,t1,A2,t2,A3,t3) | Dreiphasige exponentielle Wachstumsfunktion mit Parametern Zeitkonstante.
|
| ExpGrow1(x,y0,x0,A1,t1) | Einphasiges exponentielles Wachstum mit Zeitverschiebung, x0 sollte fest sein.
|
| ExpGrow2(x, y0, x0, A1, t1, A2, t2) | Einphasiges exponentielles Wachstum mit Zeitverschiebung, x0 sollte fest sein.
|
| ExpGrow3Dec2(x,y0,xc,Ag1,tg1,Ag2,tg2,Ag3,tg3,Ad1,td1,Ad2,td2) (2015 SR0) |
Exponentielle Funktion mit drei Wachstums- und zwei Zerfallsphasen.
|
| ExpGrowDec(x,y0,xc,Ag,tg,Ad,td) (2015 SR0) |
Exponentialfunktion mit einer Wachstums- und einer Zerfallsphase.
|
| ExpLinear(x,p1,p2,p3,p4) | Exponentielle lineare Kombination.
|
| Langevin(x,y0,xc,C) | Langevin-Funktion verwendet in Paramagnetismus mit drei Parametern.
|
| LangevinMod(x,y0,xc,C,s) (2015 SR0) |
Langevin-Funktion mit modifizierter Skala.
|
| PIPlatt(x,Pm,alpha) (2017 SR0) |
Modell der Photosynthese vs. Strahlungskurve nach Platt.
|
| PIPlatt2(x,Ps,alpha,beta) (2017 SR0) |
Modell der Photosynthese vs. Strahlungskurve mit Photoinhibition nach Platt
|
| PIWebb(x,Pm,alpha) (2017 SR0) |
Modell der Photosynthese vs. Strahlungskurve nach Webb
|
| MnMolecular(x,A,xc,k), | Monomolekulares Wachstumsmodell.
|
| MnMolecular1(x,A1,A2,k) | Eine weitere Form des monomolekularen Wachstumsmodells.
|
| Shah(x,a,b,c,r) | Exponentielle Zerfallsfunktion kombiniert mit einer linearen Funktion.
|
| Stirling(x,a,b,k) | Exponentielle Wachstumsfunktion mit Steigung bei null für Parameter.
|
| YldFert(x,a,b,r) | Ertrag-Dünger-Modell in der Landwirtschaft und Lernkurve in der Psychologie.
|
| YldFert1(x,a,b,k) | Ertrag-Dünger-Modell in der Landwirtschaft und Lernkurve in der Psychologie.
|
| Name | Brief Description |
|---|---|
| BiDoseResp(x,A1,A2,LOGx01,LOGx02,h1,h2,p) | Biphasische Dose-Response-Funktion.
|
| BiHill(x,Pm,Ka,Ki,Ha,Hi) (2015 SR0) |
Biphasische Hill-Gleichung.
|
| BoltzIV(x,vhalf,dx,gmax,vrev) | Transformierte Boltzmann-Funktion für IV-Daten.
|
| Boltzmann(x, A1, A2, x0, dx) | Boltzmann-Funktion - erzeugt eine sigmoidale Kurve.
|
| DoseResp(x,A1,A2,LOGx0,p) | Dose-Response-Kurve mit variabler Hill-Steigung gegeben durch Parameter 'p'.
|
| DoubleBoltzmann(x,y0,A,frac,x01,x02,k1,k2) | Doppelte Boltzmann-Funktion, Summe von zwei Boltzmann-Funktionen.
|
| Hill(x,Vmax,k,n) | Hill-Funktion zum Bestimmen der Ligandkonzentration und maximale Anzahl der Bindungsstellen.
|
| Hill1(x,START,END,k,n) | Modifizierte Hill-Funktion mit Verschiebung.
|
| Logistic(x, A1, A2, x0, p) | Logistische Dose-Response in Pharmakologie/Chemie. Auch als 4PL oder 4PLC bezeichnet.
|
| Logistic5(x,Amin,Amax,x0,h,s) | Logistische Funktion mit fünf Parametern. Auch als 5PL oder 5PLC bezeichnet.
|
| MichaelisMenten(x,Vmax,Km) | Michaelis-Menten-Funktion zum Beschreiben der Beziehung von der Konzentration des Substrats und der Enzymgeschwindigkeit.
|
| SGompertz(x,a,xc,k) | Gompertz-Wachstumsmodell für Populationsuntersuchungen, Tierwachstum.
|
| Slogistic1(x,a,xc,k) | Sigmoidale logistische Funktion, Typ 1.
|
| SLogistic2(x,y0,a,Wmax) | Sigmoidale logistische Funktion, Typ 2.
|
| SLogistic3(x,a,b,k) | Sigmoidale logistische Funktion, Typ 3.
|
| SRichards1(x,a,xc,d,k) | Sigmoidale Richards-Funktion, Typ 1.
|
| SRichards2(x,a,xc,d,k) | Sigmoidale Richards-Funktion, Typ 2.
|
| SWeibull1(x,A,xc,d,k) | Sigmoidale Weibull-Funktion, Typ 1.
|
| SWeibull2(x,a,b,d,k) | Sigmoidale Weibull-Funktion, Typ 2.
|
| Name | Brief Description |
|---|---|
| Dhyperbl(x,P1,P2,P3,P4,P5) | Doppelte rechteckige Hyperbelfunktion.
|
| Hyperbl(x, P1, P2) | Hyperbel-Funktion, auch das Michaelis-Menten-Modell in Enzymkinetik.
|
| HyperbolaGen(x,a,b,c,d) | Verallgemeinerte Hyperbel-Funktion.
|
| HyperbolaMod(x,T1,T2) | Modifizierte Hyperbel-Funktion.
|
| RectHyperbola(x,a,b) | Rechteckige Hyperbelfunktion.
|
| Name | Brief Description |
|---|---|
| Bradley(x,a,b) | Doppelte logarithmische Reziprokfunktion.
|
| Log2P1(x,a,b), | Zweiparametrische Logarithmusfunktion.
|
| Log2P2(x,a,b) | Logarithmische Transformationsfunktion.
|
| Log3P1(x,a,b,c) | Lineare logarithmische Transformationsfunktion.
|
| Logarithm(x,A) | Einparametrischer Logarithmus.
|
| Name | Brief Description |
|---|---|
| Asym2Sig(x,y0,xc,A,w1,w2,w3) | Asymmetrische doppelte Sigmoidalfunktion.
|
| Beta(x,y0,xc,A,w1,w2,w3) | Beta-Peakfunktion zur Verwendung in Chromatographie und Spektroskopie.
|
| Bigaussian(x,y0,xc,H,w1,w2) | Bi-Gaussian-Peakfunktion verwendet zum Anpassen asymmetrischer Peaks.
|
| CCE(x,y0,xc1,A,w,k2,xc2,B,k3,xc3) | Chesler-Cram-Peakfunktion zur Verwendung in der Chromatographie.
|
| ECS(x,y0,xc,A,w,a3,a4) | Edgeworth-Cramer-Peakfunktion zur Verwendung in der Chromatographie.
|
| Extreme(x,y0,xc,w,A) | Besonderer Fall von Funktion der Extreme, Wahrscheinlichkeitsdichtefunktion nach Gumbel.
|
| Gauss(x, y0, xc, w, A) | Flächenversion der Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Fläche) |
| GaussAmp(x,y0,xc,w,A) | Amplitudenversion der Gaussian-Peakfunktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Amplitude) |
| Gaussian(x,y0,xc,A,w) | FWHM-Version der Gaussian-Funktion. (y0 = Basis, xc = Zentrum, A = Fläche, w = FWHM) |
| GaussMod(x,y0,A,xc,w,t0) | Exponentiell modifizierte Gaussian-Peakfunktion (EMG) zur Verwendung in der Chromatographie.
|
| GCAS(x,y0,xc,A,w,a3,a4) | Gram-Charlier-Peakfunktion zur Verwendung in der Chromatografie.
|
| Giddings(x,y0,xc,w,A) | Giddings-Peakfunktion zur Verwendung in der Chromatographie.
|
| InvsPoly(x,y0,xc,w,A,A1,A2,A3) | Inverse polynomielle Peakfunktion mit Zentrum.
|
| Laplace(x,y0,a,b) | Wahrscheinlichkeitsdichtefunktion nach Laplace.
|
| Logistpk(x,y0,xc,w,A) | Logistische Peakfunktion, aich als Hubbert-Funktion bezeichnet.
|
| LogNormal(x,y0,xc,w,A) | Wahrscheinlichkeitsdichtefunktion der Zufallsvariable, deren Logarithmus normalverteilt ist.
|
| Lorentz(x, y0, xc, w, A) | Lorentz-Peakfunktion mit Glockenform und viel breiteren Enden als die Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = FWHM, A = Fläche) |
| PearsonIV(x,y0,A,m,v,alpha,lam) | Pearson-Verteilung Typ IV für negative Diskriminanten, geeignet zum Modellieren von Pull-Verteilungen.
|
| PearsonVII(x,y0,xc,A,w,m) | Die Pearson-Peakfunktion Typ VII ist eine potenzierte Lorentz-Funktion.
|
| PsdVoigt1(x,y0,xc,A,w,mu) | Pseudo-Voigt-Funktion, lineare Kombination der Gaussian-Funktion und Lorentz-Funktion. (y0 = Verschiebung, xc = Zentrum, A = Fläche, w = FWHM, mu = Profilformfaktor) |
| PsdVoigt2(x,y0,xc,A,wG,wL,mu) | Pseudo-Voigt-Funktion, lineare Kombination von Gaussian und Lorentz mit unterschiedlicher FWHM. (y0 = Verschiebung, xc = Zentrum, A = Fläche, wG = Gaussian FWHM, wL=Lorentz FWHM, mu = Profilformfaktor) |
| Voigt(x,y0,xc,A,wG,wL) | Faltung einer Gaussian-Funktion (wG für FWHM) und einer Lorentzian-Funktion.
|
| Weibull3(x,y0,xc,A,w1,w2) | Amplitudenversion der Weibull-Peakfunktion.
|
| Name | Brief Description |
|---|---|
| PWL2(x,a1,k1,xi,k2) | Stückweise lineare Funktion mit zwei Segmenten.
|
| PWL3(x,a1,k1,xi1,k2,xi2,k3) | Stückweise lineare Funktion mit zwei Segmenten.
|
| Name | Brief Description |
|---|---|
| Constant(x,y0) | Funktion mit konstanter Basislinie.
|
| Cubic(x,A,B,C,D) | Polynomial dritter Ordnung
|
| Line(x,A,B) | 3D-Linienfunktion mit Steigungen und Schnittpunkten mit der Y-Achse.
|
| LineMod(x,a,b) | Linienfunktion mit Schnittpunkt mit der X-Achse und Steigung für Parameter.
|
| Parabola(x,A,B,C) | Polynomial zweiter Ordnung
|
| Poly(x, a0, a1, a2, a3, a4, a5, a6, a7, a8, a9) | Polynomial neunter Ordnung
|
| Poly4(x,A0,A1,A2,A3,A4) | Polynomielle Funktion vierter Ordnung.
|
| Poly5(x,A0,A1,A2,A3,A4,A5) | Polynomielle Funktion fünfter Ordnung.
|
| Name | Brief Description |
|---|---|
| Allometric1(x,a,b) | Klassisches Freundlich-Modell, ist in der Allometriestudie verwendet worden.
|
| Allometric2(x,a,b,c) | Eine Erweiterung des klassischen Freundlich-Modells.
|
| Belehradek(x,a,b,c) | Potenzfunktion mit verschobenem X.
|
| BlNeld(x,a,b,c,f) | Bleasdale-Nelder-Funktion für Ertrag-Dichte-Modell.
|
| BlNeldSmp(x,a,b,c) | Vereinfachtes Bleasdale-Nelder-Modell.
|
| FarazdaghiHarris(x,a,b,c) | Farazdaghi-Harris-Modell zur Verwendung in Ertrag-Dichte-Untersuchung.
|
| FreundlichEXT(x,a,b,c) | Erweiterte Gleichung für Freundlich-Adsorptionsisotherme.
|
| Gunary(x,a,b,c) | Gunary-Gleichung für Adsorptionsisotherme.
|
| LangmuirEXT1(x,a,b,c), | Erweiterte Gleichung für Langmuir-Adsorptionsisotherme.
|
| LangmuirEXT2(x,a,b,c) | Another form of extended Langmuir adsorption isotherm equation.
|
| Pareto(x,A) | Kumulative Pareto-Verteilungsfunktion mit einem Parameter, eine Potenzgesetzwahrscheinlichkeitsverteilung.
|
| Pow2P1(x,a,b), | Skalierte Pareto-Funktion.
|
| Pow2P2(x,a,b), | Zweiparametrische Potenzfunktion.
|
| Pow2P3(x,a,b) | Pareto-Transformationsfunktion.
|
| Power(x,A) | Einparametrische Potenzfunktion.
|
| Power0(x,y0,xc,A,P) | Symmetrische Potenzfunktion mit Verschiebung.
|
| Power1(x,xc,A,P) | Symmetrische Potenzfunktion.
|
| Power2(x,xc,A,pl,pu) | Asymmetrische Potenzfunktion.
|
| Name | Brief Description |
|---|---|
| BET(x,a,b) | BET-Adsorptionsgleichung (Brunauer-Emmett-Teller).
|
| BETMod(x,a,b) | Modifiziertes BET-Modell.
|
| Holliday(x,a,b,c) | Holliday-Modell - ein Ertrag-Dichte-Modell zur Verwendung in der Landwirtschaft.
|
| Holliday1(x,a,b,c) | Erweitertes Holliday-Modell.
|
| Nelder(x,a,b0,b1,b2) | Nelder Modell - ein Ertrag-Dünger-Modell in der Agrarwirtschaft.
|
| Rational0(x,a,b,c) | Rationale Funktion mit Zähler 1. Ordnung und Nenner 1. Ordnung.
|
| Rational1(x,a,b,c) | Eine weitere Form der Funktion Rational0 mit konstantem Koeffizient im normalisierten Zähler.
|
| Rational2(x,a,b,c) | Eine weitere Form der Funktion Rational0 mit Koeffizient von x im normalisierten Nenner.
|
| Rational3(x,a,b,c) | Eine weitere Form der Funktion Rational0 mit Koeffizient von x im normalisierten Zähler.
|
| Rational4(x,a,b,c) | Eine weitere Form der Funktion Rational0 mit der Summe der Konstanten und einer Rational-Funktion.
|
| Rational5(x,a,b,c,d) | Rational-Funktion mit Zähler 1. Ordnung und Nenner 2. Ordnung.
|
| Reciprocal(x,a,b) | Zweiparametrische lineare Reziprokfunktion.
|
| Reciprocal0(x,A) | Einparametrische lineare Reziprokfunktion (Steigung).
|
| Reciprocal1(x,A) | Einparametrische lineare Reziprokfunktion (Schnittpunkt mit der Y-Achse).
|
| ReciprocalMod(x,a,b) | Eine weitere Form der Reziprokfunktion mit konstantem Koeffizient im normalisierten Nenner.
|
| Name | Brief Description |
|---|---|
| SawtoothWave(x,x0,y0,A,T) | Sawtooth-Welle, eine periodische Funktion, bestehend aus extremen asymmetrische dreieckigen Wellen.
|
| Sine(x,y0,xc,w,A) | Die Sinusiodfunktion schwingt um einen festgelegten Wert.
|
| SineDamp(x,y0,xc,w,t0,A) | Gedämpfte Sinusoid, eine Sinusfunktion, deren Amplitude mit der Zeit zerfällt.
|
| SineSqr(x,y0,xc,w,A) | Sinus-Quadrat-Funktion.
|
| SquareWave(x,a,b,x0,T) | Modifizierte Quadrat-Wellenfunktion mit Arbeitszyklus, d. h. eine periodische Welle, die übergangsweise zwischen zwei Ebenen wechselt.
|
| SquareWaveMod(x, a, b, x0, duty, T) (2016 SR0) |
Modifizierte Quadrat-Wellenfunktion mit Arbeitszyklus, d. h. ein periodische Welle, die übergangsweise zwischen zwei Ebenen wechselt.
|
| Step(x,A,B,x1) | Stückweise konstante Funktion mit zwei Segmenten.
|
| Name | Brief Description |
|---|---|
| Chebyshev2D(x,y,z0,A1,A2,B1,B2,C1) | Tschebyscheff-Reihenpolynome.
|
| Cosine(x,y,z0,A1,A2,B1,B2,C1) | Kosinus-Reihenpolynome.
|
| DoseResp2D(x,y,z0,B,C,D,E,F) | Nichtlineare logistische Dose-Response-Funktion
|
| Exponential2D(x,y,z0,B,C,D) | Exponentielle 2D-Zerfallsfunktion.
|
| Extreme2D(x,y,z0,B,C,D,E,F) | Nichtlineare Extremwertfunktion.
|
| ExtremeCum(x,y,z0,B,C,D,E,F,G,H) | Nichtlineare kumulative Extremwertfunktion.
|
| Fourier2D(x,y,z0,a,b,c,d,w1,w2) | Summe von Sinus- und Cosinusfunktionen der zwei Variablen.
|
| Gauss2D(x,y,z0,A,xc,w1,yc,w2) | Die Gaussian-Oberfläche.
|
| GaussCum(x,y,z0,B,C,D,E,F) | Kumulative 2D-Gaussian-Funktion.
|
| Gaussian2D(x,y,z0,A,xc,w1,yc,w2,theta) | Die gedrehte Gaussian-Oberfläche.
|
| LogisticCum(x,y,z0,B,C,D,E,F) | Nichtlineare Sigmoidfunktion (Logistisch Kumulativ)
|
| LogNormal2D(x,y,z0,B,C,D,E,F,G,H) | 2D-Log-Normal-Funktion.
|
| Lorentz2D(x,y,z0,A,xc,w1,yc,w2) | Nichtlineare Sigmoidfunktion (Logistisch Kumulativ)
|
| Parabola2D(x,y,z0,a,b,c,d) | 2D-Parabelfunktion ohne xy-Term.
|
| Plane(x,y,z0,a,b) | Die Ebenenoberfläche.
|
| Poly2D(x,y,z0,a,b,c,d,f) | Quadratisches 2D-Polynomial.
|
| Polynomial2D(x,y,z0,A1,A2,A3,A4,A5,B1,B2,B3,B4,B5) | 2D-Polynom 5. Ordnung ohne gekreuzte Terme.
|
| Power2D(x,y,z0,B,C,D,E,F) | 2D-Potenzfunktion.
|
| Rational2D(x,y,z0,A01,B01,B02,B03,A1,A2,A3,B1,B2) | 2D-Rational-Funktion mit Zähler 3. Ordnung und Nenner 3. Ordnung.
|
| RationalTaylor(x,y,z0,A01,B01,B02,C02,A1,A2,B1,B2,C2) | 2D-Taylor-Rational-Funktionen.
|
| Voigt2D(x,y,z0,A,xc,w1,yc,w2,mu) | Die Voigt-Oberfläche.
|
| Voigt2DMod(x,y,z0,A,xc,w1,yc,w2,mu) (2016 SR0) |
Die Voigt-Oberfläche mit Volumen als Parameter.
|
| Name | Brief Description |
|---|---|
| Asym2Sig(x,y0,xc,A,w1,w2,w3) | Asymmetrische doppelte Sigmoidalfunktion.
|
| Bigaussian(x,y0,xc,H,w1,w2) | Bi-Gaussian-Peakfunktion verwendet zum Anpassen asymmetrischer Peaks.
|
| BWF(x,y0,xc,H,w,q) | Linienform nach Breit-Wigner-Fano (BWF)
|
| CCE(x,y0,xc1,A,w,k2,xc2,B,k3,xc3) | Chesler-Cram-Peakfunktion zur Verwendung in der Chromatographie.
|
| ConsGaussian(x,y0, xc, A, w1, w2) | Beschränkte Gaussian-Funktion
|
| DoniachSunjic(x,y0, xc, H, w, a) | Doniach-Sunjic-Funktion
|
| ECS(x,y0,xc,A,w,a3,a4) | Edgeworth-Cramer-Peakfunktion zur Verwendung in der Chromatographie.
|
| FraserSuzuki(x,y0,xc,A,sig) | Asymmetrische Fraser-Suzuki-Funktion.
wobei
|
| Gauss(x, y0, xc, w, A) | Flächenversion der Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Fläche) |
| GaussAmp(x,y0,xc,w,A) | Amplitudenversion der Gaussian-Peakfunktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Amplitude) |
| Gaussian(x,y0,xc,A,w) | FWHM-Version der Gaussian-Funktion. (y0 = Basis, xc = Zentrum, A = Fläche, w = FWHM) |
| Gaussian_LorenCross(x,y0, xc, A, w, s) | Gaussian-Lorentzian-Kreuzproduktfunktion.
|
| GaussMod(x,y0,A,xc,w,t0) | Exponentiell modifizierte Gaussian-Peakfunktion (EMG) zur Verwendung in der Chromatographie.
|
| GCAS(x,y0,xc,A,w,a3,a4) | Gram-Charlier-Peakfunktion zur Verwendung in der Chromatografie.
|
| HVL(x, y0, xc, A, w, d) | Haaroff-Van-der-Linde-Funktion.
|
| InvsPoly(x,y0,xc,w,A,A1,A2,A3) | Inverse polynomielle Peakfunktion mit Zentrum.
|
| LogNormal(x,y0,xc,w,A) | Wahrscheinlichkeitsdichtefunktion der Zufallsvariable, deren Logarithmus normalverteilt ist.
|
| Lorentz(x, y0, xc, w, A) | Lorentz-Peakfunktion mit Glockenform und viel breiteren Enden als die Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = FWHM, A = Fläche) |
| PearsonVII(x,y0,xc,A,w,m) | Die Pearson-Peakfunktion Typ VII ist eine potenzierte Lorentz-Funktion.
|
| PsdVoigt1(x,y0,xc,A,w,mu) | Pseudo-Voigt-Funktion, lineare Kombination der Gaussian-Funktion und Lorentz-Funktion. (y0 = Verschiebung, xc = Zentrum, A = Fläche, w = FWHM, mu = Profilformfaktor) |
| PsdVoigt2(x,y0,xc,A,wG,wL,mu) | Pseudo-Voigt-Funktion, lineare Kombination von Gaussian und Lorentz mit unterschiedlicher FWHM. (y0 = Verschiebung, xc = Zentrum, A = Fläche, wG = Gaussian FWHM, wL=Lorentz FWHM, mu = Profilformfaktor) |
| Pulse(x,y0,x0,A,t1,P,t2) | Exponentielle Pulse-Funktion (x >= x0 ? y : 0).
|
| SchulzFlory(x,y0,xc,w,A) | Schulz-Flory-Verteilungsfunktion zum Beschreiben von relativen Verhältnissen der Polymere nach einem Polymerisationsprozess.
|
| Sine(x,xc,w,A,y0) | Die Sinusiodfunktion schwingt um einen festgelegten Wert.
|
| SineDamp(x,y0,xc,w,t0,A) | Gedämpfte Sinusoid, eine Sinusfunktion, deren Amplitude mit der Zeit zerfällt.
|
| Sinesqr(x,xc,w,A,y0) | Sinus-Quadrat-Funktion.
|
| Voigt(x,y0,xc,A,wG,wL) | Faltung einer Gaussian-Funktion (wG für FWHM) und einer Lorentzian-Funktion. (y0 = Verschiebung, xc = Zentrum, A = Fläche, wG = Gaussian FWHM, wL = Lorentz FWHM) |
| Weibull3(x,y0,xc,A,w1,w2) | Amplitudenversion der Weibull-Peakfunktion.
|
| Name | Brief Description |
|---|---|
| Constant(x,y0) | Funktion mit konstanter Basislinie.
|
| Cubic(x,A,B,C,D) | Polynomial dritter Ordnung
|
| ExpDec1(x,y0,A1,t1) | Exponentielle Zerfallsfunktion mit einer Phase und zeitkonstantem Parameter.
|
| ExpDec2(x,y0,A1,t1,A2,t2) | Exponentielle Zerfallsfunktion mit zwei Phasen und zeitkonstantem Parameter.
|
| ExpGro1(x,y0,A1,t1) | Einphasige exponentielle Wachstumsfunktion mit Parameter Zeitkonstante.
|
| ExpGrow1(x,y0,x0,A1,t1) | Einphasiges exponentielles Wachstum mit Zeitverschiebung, x0 sollte fest sein.
|
| ExpGrow2(x, y0, x0, A1, t1, A2, t2) | Einphasiges exponentielles Wachstum mit Zeitverschiebung, x0 sollte fest sein.
|
| Exponential(x,y0,A,R0) | Exponentielle Wachstumsfunktion mit dem Parameter Ratenkonstante.
|
| Hyperbl(x, P1, P2) | Hyperbel-Funktion, auch das Michaelis-Menten-Modell in Enzymkinetik.
|
| Line(x,A,B) | 3D-Linienfunktion mit Steigungen und Schnittpunkten mit der Y-Achse.
|
| MnMolecular(x,A,xc,k), | Monomolekulares Wachstumsmodell.
|
| Parabola(x,A,B,C) | Polynomial zweiter Ordnung
|
| Poly4(x,A0,A1,A2,A3,A4) | Polynomielle Funktion vierter Ordnung.
|
| Poly5(x,A0,A1,A2,A3,A4,A5) | Polynomielle Funktion fünfter Ordnung.
|
| Step(x,A,B,x1) | Stückweise konstante Funktion mit zwei Segmenten.
|
| Name | Brief Description |
|---|---|
| CCE(x,y0,xc1,A,w,k2,xc2,B,k3,xc3) | Chesler-Cram-Peakfunktion zur Verwendung in der Chromatographie.
|
| ECS(x,y0,xc,A,w,a3,a4) | Edgeworth-Cramer-Peakfunktion zur Verwendung in der Chromatographie.
|
| Gauss(x, y0, xc, w, A) | Flächenversion der Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Fläche) |
| GaussMod(x,y0,A,xc,w,t0) | Exponentiell modifizierte Gaussian-Peakfunktion (EMG) zur Verwendung in der Chromatographie.
|
| GCAS(x,y0,xc,A,w,a3,a4) | Gram-Charlier-Peakfunktion zur Verwendung in der Chromatografie.
|
| Giddings(x,y0,xc,w,A) | Giddings-Peakfunktion zur Verwendung in der Chromatographie.
|
| Name | Brief Description |
|---|---|
| BoltzIV(x,vhalf,dx,gmax,vrev) | Transformierte Boltzmann-Funktion für IV-Daten.
|
| Boltzmann(x, A1, A2, x0, dx) | Boltzmann-Funktion - erzeugt eine sigmoidale Kurve.
|
| DoubleBoltzmann(x,y0,A,frac,x01,x02,k1,k2) | Doppelte Boltzmann-Funktion, Summe von zwei Boltzmann-Funktionen.
|
| ExpDec1(x,y0,A1,t1) | Exponentielle Zerfallsfunktion mit einer Phase und zeitkonstantem Parameter.
|
| ExpDec2(x,y0,A1,t1,A2,t2) | Exponentielle Zerfallsfunktion mit zwei Phasen und zeitkonstantem Parameter.
|
| ExpDec3(x,y0,A1,t1,A2,t2,A3,t3) | Exponentielle Zerfallsfunktion mit drei Phasen und zeitkonstantem Parameter.
|
| Gauss(x, y0, xc, w, A) | Flächenversion der Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Fläche) |
| Goldman(x,b,Nao,Nai,Ki,T) | Goldman-Hodgkin-Katz-Gleichung zur Verwendung in der Zellmembranphysiologie.
|
| Hill(x,Vmax,k,n) | Hill-Funktion zum Bestimmen der Ligandkonzentration und maximale Anzahl der Bindungsstellen.
|
| Name | Brief Description |
|---|---|
| BiDoseResp(x,A1,A2,LOGx01,LOGx02,h1,h2,p) | Biphasische Dose-Response-Funktion.
|
| Biphasic(x,Amin,Amax1,Amax2,x0_1,x0_2,h1,h2) | Biphasische sigmoidale Dose-Response (logistische Gleichung mit 7 Parametern).
|
| DoseResp(x,A1,A2,LOGx0,p) | Dose-Response-Kurve mit variabler Hill-Steigung gegeben durch Parameter 'p'.
|
| MichaelisMenten(x,Vmax,Km) | Michaelis-Menten-Funktion zum Beschreiben der Beziehung von der Konzentration des Substrats und der Enzymgeschwindigkeit.
|
| OneSiteBind(x,Bmax,k1) | Einseitige direkte Bindung. Rechteckige Hyperbel, verbindet mit Isothermen- oder Sättigungskurve.
|
| OneSiteComp(x,A1,A2,logx0) | Einseitige Konkurrenzkurve. Dose-Response-Kurve mit Hill-Steigung gleich -1.
|
| TwoSiteBind(x,Bmax1,Bmax2,k1,k2) | Zweiseitige Bindungskurve.
|
| TwoSiteComp(x,A1,A2,logx0_1,logx0_2,fraction) | Zweiseitige Konkurrenzfunktion zum Beschreiben der Konkurrenz eines Liganden für zwei Rezeptortypen.
|
| Name | Brief Description |
|---|---|
| Bingham(x,y0,A) (2015 SR0) |
Bingham-Modell zum Beschreiben der viskoplastischen Flüssigkeiten, die eine Ertragsreaktion (yield response) besitzen.
|
| Cross(x,A1,A2,t,m) (2015 SR0) |
Gekreuztes Modell zum Beschreiben des pseudoplastischen Flusses mit asymptotischen Viskositäten bei null und infiniten Schergeschwindigkeiten.
|
| Carreau(x,A1,A2,t,a,n) (2015 SR0) |
Carreau-Yasuda-Modell zum Beschreiben des pseudoplastischen Flusses mit asymptotischen Viskositäten bei null und infiniten Schergeschwindigkeiten.
|
| Herschel(x,y0,K,n) (2015 SR0) |
Herschel-Bulkley-Modell zum Beschrieben von viskoplastischen Materialien, die eine Potenzgesetz-Beziehung besitzen.
|
| VFT(x,A,B,x0) (2015 SR0) |
Vogel-Fulcher-Tammann-Gleichung
|
| MYEGA(x,y0,K,C) (2015 SR0) |
Mauro-Yue-Ellison-Gupta-Allan-Gleichung
|
| Name | Brief Description |
|---|---|
| CompInhib(x,Vmax,Km,Ki,Ic) (2015 SR0) |
Kompetitives Hemmungsmodell für einzelne Substrate und einzelne Inhibitoren.
|
| NoncompInhib(x,Vmax,Km,Ki,Ic) (2015 SR0) |
Nichtkompetitives Inhibitionsmodell für einzelne Substrate und einzelne Inhibitoren.
|
| UncompInhib(x,Vmax,Km,Kia,Ic) (2015 SR0) |
Unkompetitives Inhibitionsmodell für einzelne Substrate und einzelne Inhibitoren.
|
| MixedModelInhib(x,Vmax,Km,Ki,Alpha,Ic) (2015 SR0) |
Eine allgemeine Gleichung, einschließlich kompetitiver, unkompetitiver und nichtkompetitiver Inhibition als Spezialfälle.
|
| SubstrateInhib(x,Vmax,Km,Ki) (2015 SR0) |
Substrathemmungsmodell bei hohen Konzentrationen.
|
| MichaelisMenten(x,Vmax,Km) | Michaelis-Menten-Funktion zum Beschreiben der Beziehung von der Konzentration des Substrats und der Enzymgeschwindigkeit.
|
| Hill(x,Vmax,k,n) | Hill-Funktion zum Bestimmen der Ligandkonzentration und maximale Anzahl der Bindungsstellen.
|
| Name | Brief Description |
|---|---|
| GaussAmp(x,y0,xc,w,A) | Amplitudenversion der Gaussian-Peakfunktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Amplitude) |
| InvsPoly(x,y0,xc,w,A,A1,A2,A3) | Inverse polynomielle Peakfunktion mit Zentrum.
|
| Lorentz(x, y0, xc, w, A) | Lorentz-Peakfunktion mit Glockenform und viel breiteren Enden als die Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = FWHM, A = Fläche) |
| PearsonVII(x,y0,xc,A,w,m) | Die Pearson-Peakfunktion Typ VII ist eine potenzierte Lorentz-Funktion.
|
| PsdVoigt1(x,y0,xc,A,w,mu) | Pseudo-Voigt-Funktion, lineare Kombination der Gaussian-Funktion und Lorentz-Funktion. (y0 = Verschiebung, xc = Zentrum, A = Fläche, w = FWHM, mu = Profilformfaktor) |
| PsdVoigt2(x,y0,xc,A,wG,wL,mu) | Pseudo-Voigt-Funktion, lineare Kombination von Gaussian und Lorentz mit unterschiedlicher FWHM. (y0 = Verschiebung, xc = Zentrum, A = Fläche, wG = Gaussian FWHM, wL=Lorentz FWHM, mu = Profilformfaktor) |
| Voigt(x,y0,xc,A,wG,wL) | Faltung einer Gaussian-Funktion (wG für FWHM) und einer Lorentzian-Funktion.
|
| Name | Brief Description |
|---|---|
| Exponential(x,y0,A,R0) | Exponentielle Wachstumsfunktion mit dem Parameter Ratenkonstante.
|
| ExponentialCDF(x,y0,A,mu) (2016 SR0) |
Exponentielle kumulative Verteilungsfunktion.
|
| Extreme(x,y0,xc,w,A) | Besonderer Fall von Funktion der Extreme, Wahrscheinlichkeitsdichtefunktion nach Gumbel.
|
| GammaCDF(x,y0,A1,a,b) (2016 SR0) |
Kumulative Gamma-Verteilungsfunktion.
|
| Gauss(x, y0, xc, w, A) | Flächenversion der Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Fläche) |
| GaussAmp(x,y0,xc,w,A) | Amplitudenversion der Gaussian-Peakfunktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Amplitude) |
| Gumbel(x,a,b) | Transformierte kumulative Gumbel-Verteilungsfunktion.
|
| Laplace(x,y0,a,b) | Wahrscheinlichkeitsdichtefunktion nach Laplace.
|
| Logistic(x, A1, A2, x0, p) | Logistische Dose-Response in Pharmakologie/Chemie. Auch als 4PL oder 4PLC bezeichnet.
|
| LogNormal(x,y0,xc,w,A) | Wahrscheinlichkeitsdichtefunktion der Zufallsvariable, deren Logarithmus normalverteilt ist.
|
| LognormalCDF(x,y0,A,xc,w) (2016 SR0) |
Kumulative LognormalCDF-Verteilungsfunktion.
|
| Lorentz(x, y0, xc, w, A) | Lorentz-Peakfunktion mit Glockenform und viel breiteren Enden als die Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = FWHM, A = Fläche) |
| NormalCDF(x,y0,A,xc,w) | Kumulative Normalverteilungsfunktion (y0 = Verschiebung, A = Amplitude, xc = Mittelwert, w = Standardabweichung) |
| Pareto(x,A) | Kumulative Pareto-Verteilungsfunktion mit einem Parameter, eine Potenzgesetzwahrscheinlichkeitsverteilung.
|
| Pareto2(x,a,b) | Pareto-Funktion mit zwei Parametern.
|
| PearsonIV(x,y0,A,m,v,alpha,lam) | Pearson-Verteilung Typ IV für negative Diskriminanten, geeignet zum Modellieren von Pull-Verteilungen.
|
| Poisson(x,y0,r) | Wahrscheinlichkeitsdichtefunktion nach Poisson, eine diskrete Wahrscheinlichkeitsverteilung.
|
| Rayleigh(x,b) | Kumulative Rayleigh-Verteilungsfunktion
|
| Weibull(x,y0,a,r,u) | Weibull-Wahrscheinlichkeitsdichtefunktion.
|
| WeibullCDF(x,y0,A1,a,b) (2016 SR0) |
Kumulative Weibull-Verteilungsfunktion.
|
| Name | Brief Description |
|---|---|
| Boltzmann(x, A1, A2, x0, dx) | Boltzmann-Funktion - erzeugt eine sigmoidale Kurve.
|
| DoseResp(x,A1,A2,LOGx0,p) | Dose-Response-Kurve mit variabler Hill-Steigung gegeben durch Parameter 'p'.
|
| ExpDecay1(x,y0,x0,A1,t1) | Einphasige exponentielle Zerfallsfunktion mit Zeitverschiebung, x0 sollte fest sein.
|
| ExpGrow1(x,y0,x0,A1,t1) | Einphasiges exponentielles Wachstum mit Zeitverschiebung, x0 sollte fest sein.
|
| Gauss(x, y0, xc, w, A) | Flächenversion der Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = Breite, A = Fläche) |
| Hill(x,Vmax,k,n) | Hill-Funktion zum Bestimmen der Ligandkonzentration und maximale Anzahl der Bindungsstellen.
|
| Hyperbl(x, P1, P2) | Hyperbel-Funktion, auch das Michaelis-Menten-Modell in Enzymkinetik.
|
| Logistic(x, A1, A2, x0, p) | Logistische Dose-Response in Pharmakologie/Chemie. Auch als 4PL oder 4PLC bezeichnet.
|
| Lorentz(x, y0, xc, w, A) | Lorentz-Peakfunktion mit Glockenform und viel breiteren Enden als die Gaussian-Funktion. (y0 = Verschiebung, xc = Zentrum, w = FWHM, A = Fläche) |
| Sine(x,y0,xc,w,A) | Die Sinusiodfunktion schwingt um einen festgelegten Wert.
|
| Voigt(x,y0,xc,A,wG,wL) | Faltung einer Gaussian-Funktion (wG für FWHM) und einer Lorentzian-Funktion.
|
| Name | Brief Description |
|---|---|
| GaussianLorentz(y0, xc, A1, A2, w1, w2) | Eine unabhängige und zwei abhängige Variablen, geteilte Parameter.
|
| Helix(x,x0,y0,A,w,p) | 3D-Helix-Funktion
|
| HillBurk(Vm1, Km1, Vm2, Km2) | Kombination aus Hill- und Burk-Modellen mit zwei unabhängigen und zwei abhängigen Variablen.
|
| Line3(a, b, c, d) | 3D-Linienfunktion mit Steigungen und Schnittpunkten mit der Y-Achse.
|
| LineExp(x,Vmax,k,n) | Kombination aus Linien- und Exponentialmodellen mit einer unabhängigen und zwei abhängigen Variablen.
|
| Name | Brief Description |
|---|---|
| BitAND(n1, n2) | Gibt Bit für Bit die AND-Operation von zwei ganzen Zahlen aus. |
| BitOR(n1, n2) | Gibt Bit für Bit die OR-Operation von zwei ganzen Zahlen aus. |
| BitXOR(n1, n2) | Gibt Bit für Bit die XOR-Operation von zwei ganzen Zahlen aus. |
| ISNA(d) | Bestimmt, ob die Zahl ein NANUM ist. |
| isText(str$) (2019) |
Bestimmt, ob ein Wert ein Text ist. Gibt 1 für Text und leeren Wert aus; gibt 0 für den numerischen Wert oder NANUM aus. |
| Let(var1,val1[,var2,val2,]...[,var39, val39], expression)[$] (2021) |
Ähnlich der Funktion LET() von MS Excel. Weisen Sie Werte (valN) zu Variablen (varN) für bis zu 39 Variable-Wert-Paare zu, die in expression verwendet werden. Optional wird $ bei der Ausgabe von Zeichenketten verwendet. Beispiele:
|
| NA() | Gibt NANUM aus. |
| ocolor2rgb(oColor) (2019 SR0) |
Wandelt einen internen Farbcode oColor in einen RGB-Wert um. |
| xf_get_last_error_code() | Ermittelt den letzten Wert des Fehlercodes der XFunction Engine. |
| xf_get_last_error_message()$ | Ermittelt die letzte Meldung der Fehlerzeichenkette der XFunction Engine. |
| xor(n1,n2) (2019 SR0) |
Gibt XOR-Operation von zwei logischen Werten n1 und n2 aus. Beispiel
|
| Name | Brief Description |
|---|---|
| Base(num,radix[,len])$ (2019 SR0) |
Wandelt eine gegebene ganze Zahl num in eine Zeichenkettendarstellung des festgelegten radix um. |
| Bin2Dec(str$) | Wandelt eine Binärzahl in eine Dezimalzahl um. |
| BitLShift(num,shift) (2019 SR0) |
Verschiebt eine Dezimalzahl num nach links um die festgelegte Anzahl von Bits shift. |
| BitRShift(num,shift) (2019 SR0) |
Verschiebt eine Dezimalzahl num nach rechts um die festgelegte Anzahl von Bits shift. |
| Convert(d,str1$,str2$) | Wandelt eine Zahl von einem Messsystem in ein anderes um. |
| Decimal(text$,radix) | Wandelt Zeichenkettendarstellung text im festgelegten radix in eine Dezimalzahl. |
| Dec2Bin(n)$ | Wandelt eine Dezimalzahl in eine Binärzahl um. Der Eingabebereich reicht von -512 bis 511. |
| Dec2Hex(n[,places])$ | Wandelt eine Dezimalzahl in eine Hexadezimalzahl um und legt optional die Anzahl der Zeichen fest. |
| Hex2Dec(str$) | Konvertiert die Darstellung einer Zeichenkette einer Hexadezimalzahl in Dezimal. |
| Name | Brief Description |
|---|---|
| Imabs(c) | Ermittelt das Modulo einer komplexen Zahl. |
| Imaginary(c) | Diese Funktion wird verwendet, um den imaginären Teil einer komplexen Zahl zu ermitteln. |
| Imargument(c) | Ermittelt das Argument (Theta) einer komplexen Zahl. |
| Imatan(c) (2016 SR0) |
Berechnet die inverse Tangente einer komplexen Zahl. |
| Imatanh(c) (2016 SR0) |
Berechnet den inversen hyperbolischen Tangens einer komplexen Zahl. |
| Imconjugate(c) | Ermittelt die Konjugierte einer komplexen Zahl. |
| Imcos(c) | Berechnet den Cosinuswert einer komplexen Zahl.
wobei C eine komplexe Zahl ist und |
| Imcosh(c) (2019 SR0) |
Berechnet den hyperbolischen Kosinus einer komplexen Zahl. |
| Imcot(c) (2019 SR0) |
Berechnet den Kotangens einer gegebenen komplexen Zahl. |
| Imcsc(c) (2019 SR0) |
Berechnet den Kosekans einer gegebenen komplexen Zahl. |
| Imcsch(c) (2019 SR0) |
Berechnet den hyperbolischen Kosekans einer gegebenen komplexen Zahl. |
| Imsec(c) (2019 SR0) |
Berechnet den Sekans einer gegebenen komplexen Zahl. |
| Imsech(c) (2019 SR0) |
Berechnet den hyperbolischen Sekans einer gegebenen komplexen Zahl. |
| Imsinh(c) (2019 SR0) |
Berechnet den hyperbolischen Sinus einer gegebenen komplexen Zahl. |
| Imtan(c) (2019 SR0) |
Berechnet den Tangens einer gegebenen komplexen Zahl. |
| Imdiv(c1,c2) | Berechnet die komplexe Division. |
| Imexp(c) | Berechnet den exponentiellen Wert einer komplexen Zahl.
wobei |
| Imln(c) | Berechnet den natürlichen Logarithmus der komplexen Zahl.
wobei ImAbs den Modulo der komplexen Zahl berechnet, |
| Imlog10(c) | Berechnet den Logarithmus zur Basis 10 einer komplexen Zahl.
wobei ImLn den natürlichen Logarithmus der komplexen Zahl berechnet und |
| Imlog2(c) | Berechnet den Logarithmus zur Basis 2 einer komplexen Zahl.
wobei ImLn den natürlichen Logarithmus der komplexen Zahl berechnet und |
| ImPower(c,d) | Berechnet die gegebene komplexe Zahl zur Potenz des festgelegten Werts. |
| Improduct(c1,c2) | Führt die Produktoperation (Multiplikation) der zwei komplexen Zahlen durch.
|
| ImReal(c) | Ermittelt den realen Teil der festgelegten komplexen Zahl. |
| Imsin(c) | Berechnet den Sinuswert einer komplexen Zahl.
wobei C eine komplexe Zahl ist und |
| Imsqrt(c) | Berechnet die Quadratwurzel einer komplexen Zahl. |
| ImSub(c1,c2) | Führt eine Subtraktion zwischen zwei komplexen Zahlen durch. |
| ImSum(c1,c2) | Ermittelt die Summe von zwei festgelegten komplexen Zahlen. |
| Real2Complex(real,imag) | Wandelt die festgelegten zwei realen Zahlen in eine komplexe um. Beachten Sie, dass der Datentyp der Ausgabespalte vorher auf komplex (16) gesetzt werden muss. Beispiele:
|
| Name | Brief Description |
|---|---|
| Effect(nrate,npery) | Berechnet die effektive jährliche Zinsrate. |
| Nominal(erate,npery) | Berechnet die nominale jährliche Zinsrate. |
| pDuration(rate,pv,fv) | Berechnet die Anzahl der Perioden, die erforderlich ist, damit eine Investition einen gewünschten zukünftigen Wert erreicht. |
| RRI(nper, pv, fv) | Berechnet eine äquivalente Zinsrate für das Wachstum einer Investition. |
Jede Funktion gibt entweder einen einzelnen Wert oder einen Wertebereich (einen Datensatz) aus, abhängig vom Funktionstyp und den mitgelieferten Argumenten. Wenn nicht anderweitig festgelegt, geben alle Funktionen einen Bereich aus, falls das erste Argument, das an die Funktion übergeben wird, ein Bereich ist. Wird ein Wert übergeben, geben alle Funktionen einen Wert aus.