Kaplan-Meier-Schätzer

KaplanMeier-Estimator

Einführung

Die Lebensdaueranalyse ist die Untersuchung der Zeit bis zu einem bestimmten Ereignis, z.B. dem Eintritt des Todes. Die Zeit bis zu dem Ereignis wird als Lebensdauer oder Überlebenszeit bezeichnet. Sollte das Ereignis während des Untersuchungszeitraums eintreten, stellt die Lebensdauer für das Mitglied der Untersuchungsgruppe die vollständigen Daten dar. Sollte das Ereignis für ein bestimmtes Mitglied nicht eintreten, wird die Lebensdauer als zensierte Zeit bezeichnet.

Die Überlebensrate kann als Überlebensfunktion S(t) beschrieben werden, der Anteil der Beobachtungseinheiten, die den Zeitpunkt t überleben. Eine Überlebensfunktion S(t) ist die Wahrscheinlichkeit des Überlebens für mindestens die Zeit t mit S(t)=1-F(t), wobei F(t) die kumulative Verteilungsfunktion der Ausfallzeiten ist. Da durch die zensierten Werte eine unvollständige Beobachtung vorhanden ist, sollte eine spezielle Methode zum Schätzen von S(t) eingeführt werden. Mit dem Kaplan–Meier- oder auch Produkt-Limit-Schätzer ist eine Schätzung von S(t) möglich, und zwar von einer Stichprobe der Ausfallzeiten aus, die zunehmend rechtszensiert sein kann.

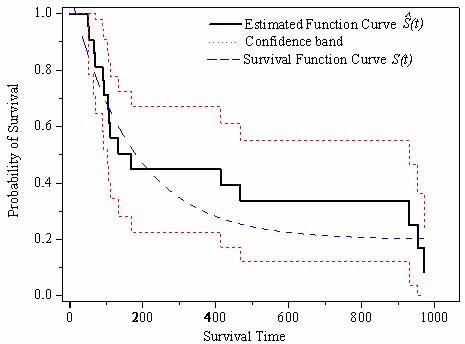
Die geschätzte Überlebensfunktion ist eine Schrittfunktion. Je mehr der Stichprobenumfang zunimmt, desto näher liegt die Kurve an der wahren Kurve S(t).

Neben der Überlebenskurve berechnet Origin auch die obere und untere Konfidenzgrenze und die Schätzung der Quartile.

Umgang mit fehlenden Werten

Wenn es fehlender Werte im Zeit-/Zensor-/Gruppierungsbereich gibt, wird der gesamte Fall aus der Analyse ausgeschlossen.

In den älteren Versionen vor Origin 2015 wurden die fehlenden Werte in dem Gruppierungsbereich als eine Gruppe betrachtet.

Kaplan-Meier-Schätzung durchführen

Zum Berechnen des Kaplan-Meier-Schätzers:

1. Wählen Sie Statistik: Lebensdaueranalyse: Kaplan-Meier-Schätzer. Der Dialog kaplanmeier wird geöffnet.
2. Legen Sie die Eingabedaten, einschließlich den Zeitbereich und Zensorbereich, und optional die Gruppenvariable fest. Sie können auch mehrere Lebensdauertabellen festlegen, wie für die Zusammenfassung von Ereignis- und Zensorwerten sowie eine Tabelle für Überlebensschätzungen, Quartilschätzungen bzw. Mittelwertschätzungen. Wenn eine Gruppierungsvariable existiert, können Sie einen Gleichheitstest für die Überlebensfunktionen durchführen, einschließlich der Log-Rank-, Breslow- und Tarone-Ware-Methoden.
3. Wenn Sie auf OK klicken, wird ein Analysebericht erzeugt, der die gewünschten Tabellen enthält.

Relevante Dokumentation: nag_prod_limit_surviv_fn (g12aac).